Huge Mods UVA - 10692（指数循环节）

题意：

输入正整数a1,a2,a3..an和模m，求a1^a2^...^an mod m

解析：

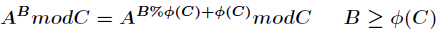
#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;
LL A[maxn], num[maxn];
LL n;
char str[maxn];
LL qpow(LL a, LL b, LL m)
{
    LL res = ;
    while(b)
    {
        if(b & ) res = res * a % m;
        a = a * a % m;
        b >>= ;
    }
    return res;
}

void init()
{
    for(int i=; i<maxn; i++)
        A[i] = i;
    for(int i=; i<maxn; i++)
        if(A[i] == i)
            for(int j=i; j<maxn; j+=i)
                A[j] = A[j]/i*(i-);
}

LL dfs(LL cnt, LL m)
{
    if(cnt == n-)
    {
        return num[cnt] % m;
    }
    LL phi = A[m];
    LL k = dfs(cnt+, phi) + phi;  //因为在上一步的快速幂中已经%phi 所有这一步不用%phi
    return qpow(num[cnt], k, m);
}

int main()
{
    init();
    int kase = ;
    while(scanf("%s",str) && strcmp(str, "#"))
    {
        LL MOD;
        sscanf(str,"%lld", &MOD);
        cin>> n;
        for(int i=; i<n; i++)
        {
            cin>> num[i];
        }
        printf("Case #%d: %lld\n",++kase,dfs(, MOD));
    }
    return ;
}