●UOJ 131 [NOI2015] 品酒大会

题链：

http://uoj.ac/problem/131

题解：

网上大多数的方法都是用并查集维护。
这里呢，给出另一种自己YY的解法（但实际上本质差不多吧）:

后缀数组，RMQ，单调栈

1).预处理
1].首先对字符串后缀排序，得到 sa[i],rank[i],height[i]
   
2].然后维护出 L[i]:表示在后缀数组中，排名最小(记其排名为 L[i])的后缀与排名为 i的后缀的LCP>=hei[i]
    同理 R[i]:表示在后缀数组中，排名最大(记其排名为 R[i])的后缀与排名为 i的后缀的LCP>hei[i]（注意这里没有'='，避免重复）
    这两个数组可以用单调栈 O(n)维护出来。
   
3].把输入的权值数组(A数组)按照排好序的后缀的顺序重新排序，得到 B数组：B[i]=A[sa[i]];
    话句话说吧：B[i]表示 排名第i的后缀的首字母对应的权值
    然后对 B数组建两个 ST表，一个用于询问区间最大值，一个用于询问区间最小值。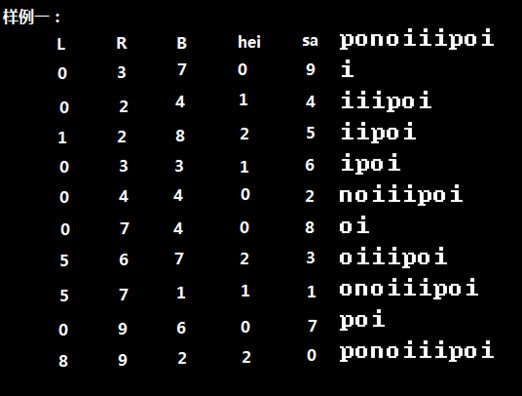

2).贡献答案
记 num[i]表示相似值为 i的方案数（询问一），val[i]表示相似值为 i的最大美味度（询问二）。
    
不难发现，L[i],R[i]数组可以理解为 在后缀数组的 [L[i],R[i]]这个区间中，hei[i]为最小值。
那么这意味着，区间[L[i],i-1]中的任意一个后缀与区间[i,R[i]]中的任意一个后缀的 LCP==hei[i]
那么便可以贡献答案了：num[hei[i]]+=(i-L[i])*(R[i]-i+1)

同时查询 ST表，得到区间[L[i],i-1]的最大最小权值 max1,min1,以及区间[i,R[i]]最大最小权值 max2,min2。
那么：val[hei[i]]=max(val[hei[i]],max(max1*max2,min1*min2))

(因为有负数，所以要考虑最小值的相乘)
   
注意到以上贡献的值都是建立在 LCP（最长公共前缀）上的，
但还有 LCP-1，LCP-2，LCP-3......这些没有被贡献到，
所以就要最后反向遍历一下两个答案数组，用后面的去更新前面的：
    num[i]+=num[i+1]; val[i]=max(val[i],val[i+1]);

然后就没了。（第一道独立且一遍 AC的 NOI题目，虽然题有点水，但还是偷乐一下咯。）

除开倍增算法和求ST表的复杂度 O(N)

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 300500
#define filein(x) freopen(#x".in","r",stdin);
#define fileout(x) freopen(#x".out","w",stdout);
using namespace std;
char S[MAXN];
int A[MAXN],B[MAXN];
int sa[MAXN],rak[MAXN],hei[MAXN],log2[MAXN],L[MAXN],R[MAXN];
struct ST{
	int st[MAXN][20];
	void Make(int N,int *val,bool type){//0:小 1：大
		for(int i=0;i<N;i++) st[i][0]=val[i];
		for(int k=1;k<=log2[N];k++)
			for(int i=(1<<k)-1;i<N;i++)
				st[i][k]=type?max(st[i-(1<<(k-1))][k-1],st[i][k-1]):
							  min(st[i-(1<<(k-1))][k-1],st[i][k-1]);
	}
	int query(int l,int r,bool type){
		static int k;
		k=log2[r-l+1];
		return type?max(st[l+(1<<k)-1][k],st[r][k]):
					min(st[l+(1<<k)-1][k],st[r][k]);
	}
}BTMAX,BTMIN;
void build(int N,int M){
	static int cc[MAXN],ta[MAXN],tb[MAXN],*x,*y,h,p;
	x=ta; y=tb; h=0;
	for(int i=0;i<M;i++) cc[i]=0;
	for(int i=0;i<N;i++) cc[x[i]=S[i]]++;
	for(int i=1;i<M;i++) cc[i]+=cc[i-1];
	for(int i=N-1;i>=0;i--) sa[--cc[x[i]]]=i;
	for(int k=1;p=0,k<N;k<<=1){
		for(int i=N-k;i<N;i++) y[p++]=i;
		for(int i=0;i<N;i++) if(sa[i]>=k) y[p++]=sa[i]-k;
		for(int i=0;i<M;i++) cc[i]=0;
		for(int i=0;i<N;i++) cc[x[y[i]]]++;
		for(int i=1;i<M;i++) cc[i]+=cc[i-1];
		for(int i=N-1;i>=0;i--) sa[--cc[x[y[i]]]]=y[i];
		swap(x,y); y[N]=-1; x[sa[0]]=0; M=1;
		for(int i=1;i<N;i++)
			x[sa[i]]=y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k]?M-1:M++;
		if(M>=N) break;
	}
	for(int i=0;i<N;i++) rak[sa[i]]=i;//puts(S+sa[i]);
	for(int i=0,j;i<N;i++){
		if(h) h--;
		if(rak[i]){
			j=sa[rak[i]-1];
			while(S[i+h]==S[j+h]) h++;
		}
		hei[rak[i]]=h;
	}
}
void preLR(int N){
	static int stk[MAXN],stp[MAXN],top;
	top=0; stp[top]=0;
	for(int i=0;i<N;i++){
		while(top&&stk[top]>=hei[i]) top--;
		L[i]=stp[top]; top++;
		stk[top]=hei[i]; stp[top]=i;
	}
	top=N; stp[top]=N;
	for(int i=N-1;i>=0;i--){
		while(top<N&&stk[top]>hei[i]) top++;
		R[i]=stp[top]-1; top--;
		stk[top]=hei[i]; stp[top]=i;
	}
	/*for(int i=0;i<N;i++) printf("%d ",L[i]);printf("\n");
	for(int i=0;i<N;i++) printf("%d ",R[i]);printf("\n");*/
}
void getans(int N){
	static long long num[MAXN],val[MAXN],min1,min2,max1,max2;
	memset(val,0xcc,sizeof(val));
	for(int i=1;i<N;i++){
		num[hei[i]]+=1ll*(i-L[i])*(R[i]-i+1);
		min1=BTMIN.query(L[i],i-1,0);
		min2=BTMIN.query(i,R[i],0);
		max1=BTMAX.query(L[i],i-1,1);
		max2=BTMAX.query(i,R[i],1);
		val[hei[i]]=max(val[hei[i]],max(1ll*min1*min2,1ll*max1*max2));
	}
	for(int i=N-2;i>=0;i--){
		num[i]+=num[i+1];
		val[i]=max(val[i],val[i+1]);
	}
	for(int i=0;i<N;i++){
		if(!num[i]) val[i]=0;
		printf("%lld %lld\n",num[i],val[i]);
	}
}
int main()
{
	//filein(ex_savour); fileout(ex_savour);
	int N; log2[1]=0;
	for(int i=2;i<=300000;i++) log2[i]=log2[i>>1]+1;
	scanf("%d",&N); scanf("%s",S);
	for(int i=0;i<N;i++) scanf("%d",&A[i]);
	build(N,300);
	for(int i=0;i<N;i++) B[i]=A[sa[i]];
	BTMIN.Make(N,B,0);
	BTMAX.Make(N,B,1);
	preLR(N); getans(N);
	return 0;
}