【BZOJ 3561】 DZY Loves Math VI

题目：

　　给定正整数n,m。求

 

题解：

　　水题有益身心健康。(博客园的辣鸡数学公式)

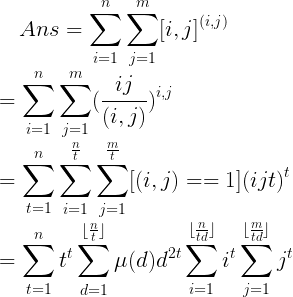
　　其实到这我想强上伯努利数，然后发现$n^2$的伯努利数，emmmmmm

　　发现这个式子可以算时间复杂度，emmmmm。积了个分发现时间复杂度很优秀啊（大概也就是$nlog$级别的）。

　　所以直接算就好了。

　　P.S.想卡卡常刷一个题榜rank1，emmmm发现自己没这个天赋。

代码：

 #define Troy

 #include "bits/stdc++.h"

 using namespace std;

 const int mod=,N=5e5+;

 inline int powmod(int a,int b){
     int ret=;
     while(b){
         if(b&) ret=ret*1ll*a%mod;
         b>>=;
         a=a*1ll*a%mod;
     }return ret;
 }

 int prim[N],num,mu[N],vis[N],sum[N],ans,f[N];

 inline int calc(int n,int m,int t){
     register int i,j;
     int ret=;
     for (i=;i<=m;++i){
         f[i]=f[i]*1ll*i%mod;
         vis[i]=mu[i]*(f[i]*1ll*f[i]%mod);
         vis[i]+=vis[i-];
         vis[i]%=mod;
         sum[i]=sum[i-]+f[i];
         sum[i]%=mod;
     }
     for (i=;i<=n;i=j+){
         j=min(n/(n/i),m/(m/i));
         ret=(ret+(vis[j]-vis[i-])*1ll*sum[n/i]%mod*sum[m/i])%mod;
     }
     return ret;
 }

 int main(){
     int n,m;
     scanf("%d%d",&n,&m);
     if(n>m) swap(n,m);
     register int i,j;
     for(i=,mu[]=;i<=n;++i){
         if(!vis[i]) {
             mu[i]=-,prim[++num]=i;
         }for(j=;prim[j]*i<=n;++j){
             vis[i*prim[j]]=true;
             if(i%prim[j]==)    {
                 mu[i*prim[j]]=;break;
             }mu[i*prim[j]]=-mu[i];
         }
     }
     for(i=;i<=m;++i)   f[i]=;
     for(i=;i<=n;++i){
         ans=(ans+powmod(i,i)*1ll*calc(n/i,m/i,i))%mod;
     }
     printf("%d\n",ans);
 }