洛谷P4391 [BOI2009]Radio Transmission 无线传输——题解
假如我们有一个用于循环连接的最短串ans,考虑用它造出来的数据(即输入的字符串s)有什么特点。发现:ans自我连接出一个大串z后从中取出的一个子串即为s,对s造一个KMP算法中的next数组,n-next[n]即为ans的长度(n为字符串s的长度)。
为什么?因为ans在s串中开头的那个字母一定会多次作为ans中的同一部分(或说同一位置)出现(否则s串就要比ans还要短(自己从纸上写个串就知道了),那么它自己就比ans更优(更短)了(这时让s串自己作为答案都要比让ans作为答案更优),显然不合理),设s[0]在ans中的正确位置(在z取出s前的那个ans循环节中的位置)为j,那么造next[n]的时候s串自我匹配时s[0]匹配到的一定是s串中紧接着下一个在ans中位置为j的字母c。设c在s串中的位置为w,那么s串w位置往后的所有字母都会被匹配到(因为s串是一个由循环子串组成的串的子串)。此时n-next[n]就是s[0]到c的之间(左闭右开)的字符串a的长度。显然因为c是s[0]在s串中紧接着下一个在ans中位置为j的字母,所以s[0]和c之间隔着的字符串的长度就是ans的长度。
代码很好写,只要按照KMP算法的模板处理出next[n],输出n-next[n]就行了,这里不多赘述。
洛谷P4391 [BOI2009]Radio Transmission 无线传输——题解的更多相关文章
- 洛谷P4391 [BOI2009]Radio Transmission 无线传输
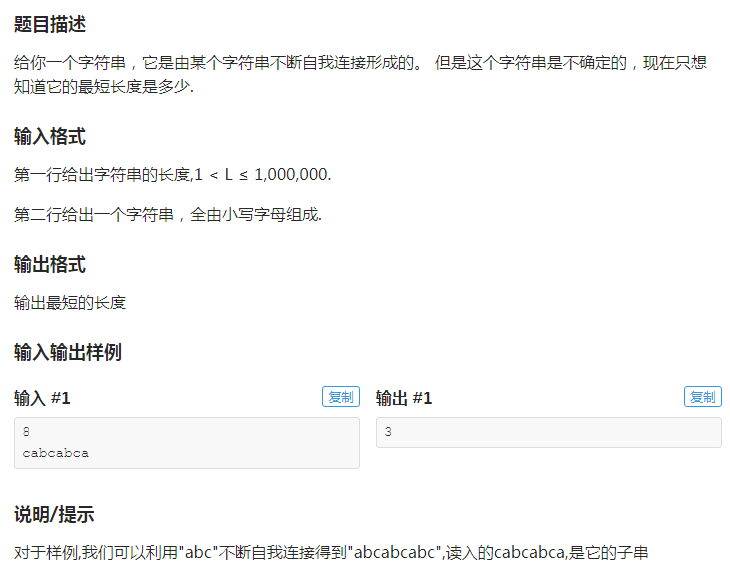
(https://www.luogu.org/problemnew/show/P4391) 题目描述 给你一个字符串,它是由某个字符串不断自我连接形成的. 但是这个字符串是不确定的,现在只想知道它的最 ...
- 洛谷 P4391 [BOI2009]Radio Transmission 无线传输
题目传送门 解题思路: 本题所要求的循环节,其实就是最长公共前缀的前缀长度减去前后缀重叠的一部分 AC代码: #include<iostream> #include<cstdio&g ...
- 【题解】洛谷P4391 [BOI2009] Radio Transmission(KMP)
洛谷P4391:https://www.luogu.org/problemnew/show/P4391 思路 对于给定的字符串 运用KMP思想 设P[x]为前x个字符前缀和后缀相同的最长长度 则对于题 ...
- P4391 [BOI2009]Radio Transmission 无线传输
P4391 [BOI2009]Radio Transmission 无线传输 kmp 题目让我们求一个串的最小循环子串 我们回想一下kmp中的失配函数 用 f 数组保存当前字符匹配失败后,需要跳到的前 ...
- 【题解】Luogu P4391 [BOI2009]Radio Transmission 无线传输
原题传送门 这题需要用到kmp匹配 推导发现: 设循环节的长度为x,那么kmp数组前x个都是0,后面kmp[x+n]=n 先求出kmp数组 答案实际就是len-kmp[len] #include &l ...
- P4391 [BOI2009]Radio Transmission 无线传输(KMP)
题目描述 给你一个字符串,它是由某个字符串不断自我连接形成的. 但是这个字符串是不确定的,现在只想知道它的最短长度是多少. 输入输出格式 输入格式: 第一行给出字符串的长度,1 < L ≤ 1, ...
- P4391 [BOI2009]Radio Transmission
描述: 给你一个字符串,它是由某个字符串不断自我连接形成的. 但是这个字符串是不确定的,现在只想知道它的最短长度是多少. 输入格式: 第一行给出字符串的长度,1 < L ≤ 1,000,000. ...
- [BOI2009]Radio Transmission 无线传输
题目描述 给你一个字符串,它是由某个字符串不断自我连接形成的. 但是这个字符串是不确定的,现在只想知道它的最短长度是多少. 输入输出格式 输入格式: 第一行给出字符串的长度,1 < L ≤ 1, ...
- Luogu4391 [BOI2009]Radio Transmission 无线传输 (KMP)
\(最小循环节\) \(=\) \(lenghth - next[lenghth]\) #include <iostream> #include <cstdio> #inclu ...
随机推荐
- ssh远程登录过程中卡住
1.首先排查网络连通性,查看网络是否通畅,远程端口是否开放 2.查看服务器复制,cpu,内存负载是否过大 3.检查ssh配置,查看以下配置是否这样配置 UseDNS no GSSAPIAuthenti ...
- 安装CentOS7虚拟机
基础环境 Windows 10 VMware Workstation 1.下载CentOS7镜像 https://www.centos.org/download/ 此次安装使用的版本为: CentOS ...
- [2019徐州网络赛J题]Random Access Iterator
题目链接 大致题意:从根节点出发,在节点x有son[x]次等概率进入儿子节点,求到达最深深度的概率.son[x]为x节点的儿子节点个数. 又又又又没做出来,心态崩了. 下来看了官方题解后发觉自己大体思 ...
- ThinkPHP5 与 composer
我是通过安装composer来获取tp5安装的,也是学习一下 在 Windows 中,你需要下载并运行 Composer-Setup.exe. 安装时,要选择本地环境中php.exe作为跟目录,这个可 ...
- P2294 [HNOI2005]狡猾的商人(差分约束)
P2294 [HNOI2005]狡猾的商人 对于每个$(x,y,w)$,连边$(x-1,y,w),(y,x-1,-w)$,表示前$y$个月的收益比前$x-1$个月的收益大$w$ 这样题目就转化为询问图 ...
- html的图片移动(js)
<!DOCTYPE html><html><style> *{padding: 0;margin: 0} #open{ width: 300px; height: ...
- 一、JsonTree
一.JsonTree [ {"id":"4","pid":"1","name":"大家电& ...
- python二维码模块(qrcode)
qrcode模块安装 运行命令行工具(cmd),使用pip安装工具分别安装qrcode. pip install qrcode 先来个简单的例子 import qrcode # 二维码内容 data ...
- Codeforces 934 最长不递减子序列 多项式系数推导
A B C 给你一个长度为N的01串 你可以翻转一次任意[L,R]的区间 问你最长的不递减序列为多少长 处理出1的前缀和 和2的后缀和 然后N^2 DP 处理出 [L,R]区间的最长不递增序列 #in ...
- 欧拉降幂公式 Super A^B mod C
Description Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=100000 ...
