吴恩达机器学习(二) 单变量线性回归(Linear Regression with one variable)
一、模型表示
1.一些术语
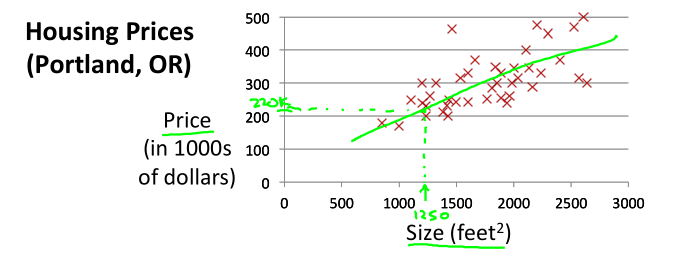
如下图,房价预测。训练集给出了房屋面积和价格,下面介绍一些术语:
x:输入变量或输入特征(input variable/features)。
y:输出变量或目标变量(output variable/target variable)。
(x, y):一个训练样本
(x(i), y(i)):第i个训练样本
m:样本数目

2.机器学习的一般过程
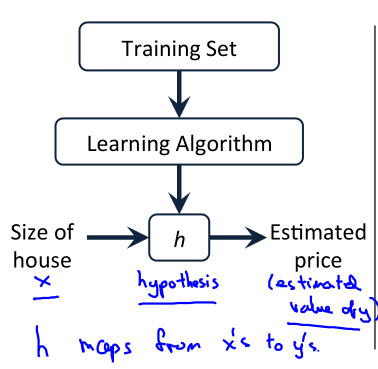
如图,机器学习算法通过学习训练集得出假设函数h(Hypothesis),然后接受输入x,输出y。假设函数h称为模型。
3.线性回归问题的假设函数
通过观察,我们使用的房价预测数据近似一条直线,所以我们将假设函数设为 h(x) = θ0 + θ1x,我们的目标是尽可能得使直线与训练集数据拟合。现阶段我们通过观察来假设函数模型,以后我们可以直接假设一个较为复杂的函数,然后通过正则化避免过拟合问题,这部分之后会讲。
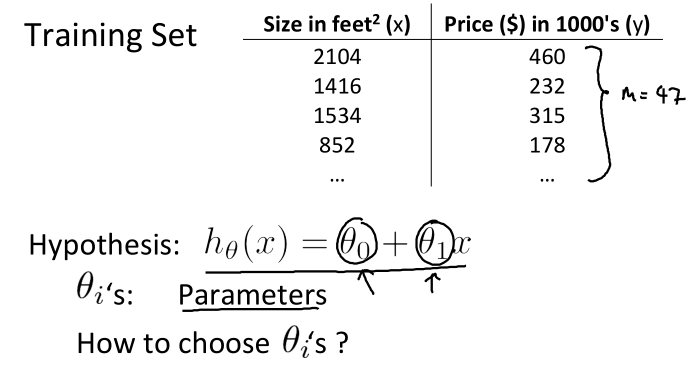
综上,我们得到假设函数:h(x) = θ0 + θ1x。这样问题就转变为求解θ0和θ1,使得曲线(或直线)h(x) 拟合训练数据。
二、代价函数(Cost Function)
1.代价函数推导与表示
从我们的目标出发,我们的目标是使曲线h(x) 拟合训练数据。从这点我们可以看出应该让训练数据尽可能的通过h(x)或离h(x)接近,故我们让y和h(x)的距离尽可能小,可以用减法运算来表示距离d,由于d有可能小于0,会使得代价函数J(θ0, θ1)反而变小,而实际上h(x)与y还是有距离的,故使用d2来表示。其中(x, y)为某一样本。
d2 = [h(x) - y]2
这样,我们将所有的样本所求出的预测值h(x)与y相减得到d,然后对所有的d求和就得到预测值与所有样本的距离的和,记为J(θ0, θ1),如下:
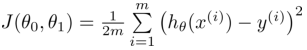
该公式称为h(x)的代价函数(Cost Function),又称平方误差函数(Squared Error Function)。上述公式是距离的平方再求和,这和相减的效果是一样的,样本数量为m,前面乘以1/m求平均值,分母的2主要是为了便于之后求导约掉。为使h(x)与y尽可能的接近,函数J(θ0, θ1)应尽可能小,故目标转变为求出使得函数J(θ0, θ1)尽可能小的θ0和θ1。即
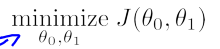
2.理解代价函数
为简化问题,我们将θ0置为0,这样,h(x) = θ1x,J也变为J(θ1)

观察下图,当θ1的值变化时,J(θ1)也跟着变化,可以观察到,当θ1= 0时h(x)与训练数据拟合的最好时,J(θ1)达到最小值。

从上面我们可以观察到函数J(θ1)为凸函数,并且对于线性回归问题,该函数只存在全局最小值,不存在局部最小值。这样,我们可以利用导数来求解极小值,同时也是最小值。
对于J(θ0, θ1)和J(θ1)同理,在绘制θ0与J(θ0, θ1)的关系时只需将θ1视为不变即可,并且求导时变为分别求J(θ0, θ1)对θ0和θ1的偏导数。
综上,我们明白了为使h(x)与训练数据拟合,必须求出使得J(θ0, θ1)最小的θ0和θ1,还知道了J(θ0, θ1)是凸函数,可以通过求导来求出最小值和对应的θ0和θ1。
三、梯度下降算法(Gradient Descent)
1.公式
上一节我们讲了可以使用导数的方式来求解θ0和θ1,本节的梯度下降算法利用的便是这种思想,其算法如下:

上述公式中α为学习率,该参数可以控制θ的变化速率。值得注意的是,在更新多个θ时要同步更新,不能先更新任意一个。
2.理解
上述公式初看可能难以理解,我们依旧使用简化的假设函数h(x) = θ1x和J(θ1)来解释。
如下图,当θ1位于极小值的右方时,J(θ1)单调增加,故 大于0,这表明函数θ1正位于最小值的右方,要达到最小值应该要减小θ1,应该减去一个正数。故下面的公式会使得θ1接近最小值:
大于0,这表明函数θ1正位于最小值的右方,要达到最小值应该要减小θ1,应该减去一个正数。故下面的公式会使得θ1接近最小值:
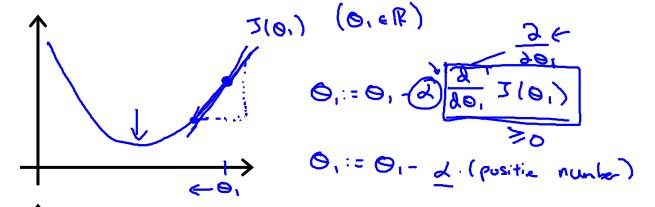
同理,当θ1位于极小值的左方时,J(θ1)单调减少故 小于0,这表明函数θ1正位于最小值的左方要达到最小值应该要增加θ1,应该加上一个正数,即减去一个负数。故下面的公式会使得θ1接近最小值:
小于0,这表明函数θ1正位于最小值的左方要达到最小值应该要增加θ1,应该加上一个正数,即减去一个负数。故下面的公式会使得θ1接近最小值:
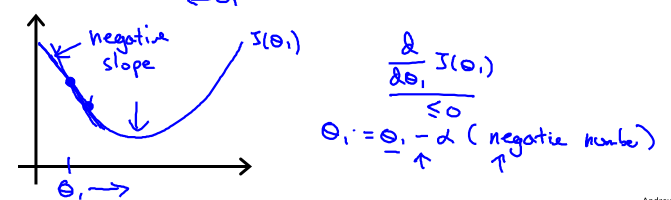
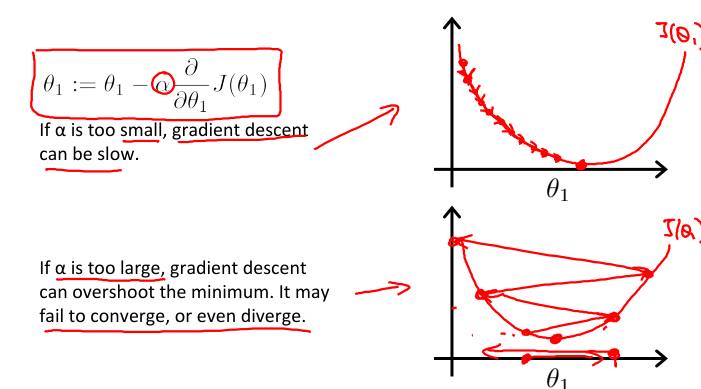
3.学习率α
对于J(θ1),我们求解θ1的公式是
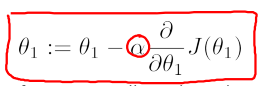
可以看到,若学习率α很小,那么θ1会很缓慢地减小;若学习率α很大,那么θ1变化会很大,甚至于越过了J(θ1)最小值对应的θ1,其在图像上表现为反复横跳,最终甚至无法收敛到最小值。如下图所示:
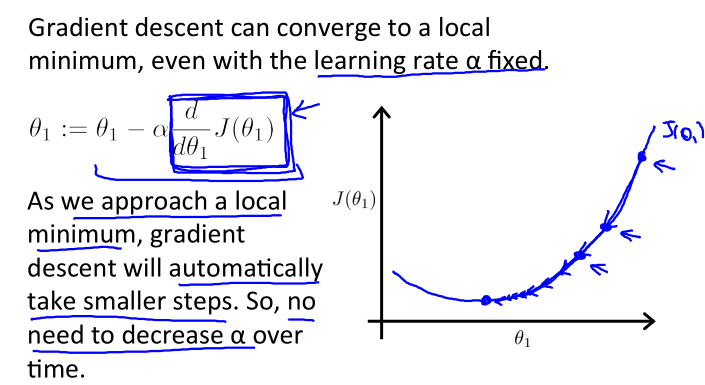
再思考,在上述求解θ1的公式中,我们是否需要在运行过程中定期修改α的值?
答案是不用。由于公式中的导数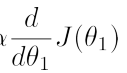 越接近极小值(同时是最小值)时会越来越小,对应到图像上表现为越来越平缓,所以
越接近极小值(同时是最小值)时会越来越小,对应到图像上表现为越来越平缓,所以 会越来越小,故θ1的变化越来越慢,直至收敛到使J(θ1)取得最小值。
会越来越小,故θ1的变化越来越慢,直至收敛到使J(θ1)取得最小值。
四、单变量线性回归问题求解
综合上述所有知识,我们得到如下总结:

我们首先假设了假设函数h(x) = θ0 + θ1x,然后为了求解θ0 和 θ1,我们从使得h(x) 拟合训练数据的想法出发,想到要使h(x) 与训练数据拟合,必须使得预测值h(x)与y的距离尽可能接近,故得到函数J(θ0 , θ1),问题转变为了求出使得最小化J(θ0 , θ1)对应的θ0 和 θ1,再从函数J(θ0 , θ1)为凸函数的特点出发,想到其在不同位置的导数正负不同,得到梯度下降算法。这样便可以使用梯度下降算法求得θ0 和 θ1,从而得到h(x)。现在问题只剩下一个,那就是求解 ,结合J(θ0 , θ1)的表达式求导,可以得到
,结合J(θ0 , θ1)的表达式求导,可以得到

这样,我们便求解了单变量线性回归问题,得到了拟合了数据的假设函数h(x)。
上述的梯度下降算法称为批量梯度下降(Batch Gradient Descent),所谓批量指的是在每一次梯度下降的过程中都使用了全部样本。
吴恩达机器学习(二) 单变量线性回归(Linear Regression with one variable)的更多相关文章
- 吴恩达机器学习笔记1-单变量线性回归(Linear Regression with One Variable)
在监督学习中我们有一个数据集,这个数据集被称训练集.
- 吴恩达机器学习笔记8-多变量线性回归(Linear Regression with Multiple Variables)--多维特征
我们探讨了单变量/特征的回归模型,现在我们对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型,模型中的特征为(
- 机器学习 (一) 单变量线性回归 Linear Regression with One Variable
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...
- Ng第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 2.4 梯度下降 2.5 梯度下 ...
- 斯坦福第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 I 2.4 代价函数的直观理解 I ...
- [Machine Learning] 单变量线性回归(Linear Regression with One Variable) - 线性回归-代价函数-梯度下降法-学习率
单变量线性回归(Linear Regression with One Variable) 什么是线性回归?线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方 ...
- 机器学习(二)--------单变量线性回归(Linear Regression with One Variable)
面积与房价 训练集 (Training Set) Size Price 2104 460 852 178 ...... m代表训练集中实例的数量x代表输入变量 ...
- Coursera《machine learning》--(2)单变量线性回归(Linear Regression with One Variable)
本笔记为Coursera在线课程<Machine Learning>中的单变量线性回归章节的笔记. 2.1 模型表示 参考视频: 2 - 1 - Model Representation ...
- 单变量线性回归(Linear Regression with One Variable)与代价函数
所谓的单变量线性回归问题就是监督学习的一部分. 通过构建数学模型给出一个相对准确的数值,也就是预测模型,通过将数据通过数学模型,衍生至回归问题 通过以下的几个例子,我们来研究单变量线性回归. 1.王阿 ...
随机推荐
- 【译文】Git merge 和 Git rebase比较
[译文]Git merge 和 Git rebase比较 原创: 胡江华 胡同学和朋友们的成长日记 2017-03-22 git rebase 这个命令经常被人认为是一种Git巫术,初学者应该避而远之 ...
- robotframework 使用Chrome手机模拟器两种方法
Open Google Simulator1 ${device metrics}= Create Dictionary width=${360} height=${640} pixelRatio=${ ...
- 配置文件加载位置与多profile文件
一. 我们在编写配置文件时,文件名可以是: application-{profile}.properties 例如:我们有几个配置文件对应的是项目不同时期的配置文件 1.application-sit ...
- java数据结构3--List
List 1.1 list接口的简介 1.2 list实现子类 ArrayList:线程不安全,查询速度快,底层用的是数组,增删慢LinkedList:线程不安全,链表结构,增删速度快,查询慢Vect ...
- 对items函数的理解
老师:dict的items应该是把dict转成列表,每个列表元素是一个包含key ,value的dict,元素应该是元组, {a:1, b:2, c:3} [(a, 1), (b,2), (c, ...
- 关于web网页截图的问题(html2canvas插件)
import html2canvas from 'html2canvas' import jpg from '@/assets/1.jpg'; htmlToImage=(element, ca ...
- Python:日期表达的转换(day of year & year month day)
我们常用的日期格式是“年月日”型的,即year-month-day,比如今天是2019年9月14日,2019-09-14. 然而,有些地方,比如遥感图像下载的命名里面,为了数据表示方便,常常是doy( ...
- JAVA笔记25-IO流(3)-处理流举例
处理流类型: 1.缓冲流 例1: import java.io.*; public class TestBufferStream{ public static void main(String arg ...
- 对elementui整体设计分析-------引用
1.需求分析 丰富的 feature:丰富的组件,自定义主题,国际化. 文档 & demo:提供友好的文档和 demo,维护成本小,支持多语言. 安装 & 引入:支持 npm 方式和 ...
- bing 精美壁纸获取方式
右键检查 打开就行了
