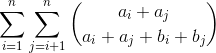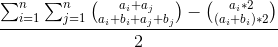AGC001[BCDE] 题解

A没意思 F太难 所以大概近期的AGC题解都是BCDE的

然后特殊情况再说

开始刷AGC的原因就是计数太差 没有脑子 好几个学长都推荐的AGC所以就开始刷了 = =

大概两天三篇的速度？【可能也就最开始几天能有这个速度= =】

好了不多说了 开始题解

————————我是分割线————————

B - Mysterious Light

比较有趣 画几个图就发现每次去掉两条就是平行四边形 除了第一次的两条不一样长以外 其他的都还是一样长的 然后就得到了一个类欧几里得的算法 那么把减法变成取模就搞定了= =

直接上代码好了 时间复杂度应该是O(lgn)吧

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define inf 20021225
#define ll long long
using namespace std;

ll N,x,ans;

int main()
{
	scanf("%lld%lld",&N,&x);
	ans+=N; ll a=x,b=N-x,tmp;
	while(a && b)
	{
		if(a>b)	swap(a,b);
		tmp = b/a*a;
		//printf("%lld %lld %lld\n",a,b,tmp);
		b%=a;	ans+=2*tmp;
		if(!b)	ans-=a;
	}
	printf("%lld\n",ans);
	return 0;
}

C - Shorten Diameter

比较直接的一个题 很明显每次删叶子 是可以贪心的 直接统计每个点和其他点距离>k的有几个 然后set维护暴力删就可以了

预处理一下dis数组比较方便 如果倍增LCA应该也可以吧 但是多个log怕不是会T

附代码。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<set>
#define inf 20021225
#define ll long long
#define mxn 2010
#define mp make_pair
#define fs first
#define se second
#define pa pair<int,int>
using namespace std;

struct edge{int to,lt;}e[mxn<<1];
int f[mxn][mxn],in[mxn],cnt,d[mxn];
int n,k;bool del[mxn];
set<pa> st;
void add(int x,int y)
{
	e[++cnt].to=y;e[cnt].lt=in[x];in[x]=cnt;
	e[++cnt].to=x;e[cnt].lt=in[y];in[y]=cnt;
}

void dfs(int x,int fa,int rt)
{
	for(int i=in[x];i;i=e[i].lt)
	{
		int y=e[i].to;if(y==fa) 	continue;
		f[rt][y]=f[rt][x]+1; dfs(y,x,rt);
	}
}

void getdis()
{
	for(int i=1;i<=n;i++)	dfs(i,i,i);
}

void work()
{
	int ans=0,x,tmp;	getdis();
	for(int i=1;i<=n;i++)
	{
		tmp=0; if(d[i]!=1)	continue;
		for(int j=1;j<=n;j++)
			if(f[i][j]>k)	tmp++;
		st.insert(mp(tmp,i));
	}
	while(!st.empty())
	{
		set<pa>::iterator it=--st.end(); pa mx=*it;
		if(mx.fs<=0)	break;
		del[mx.se]=1; st.erase(it);	x=mx.se;
		for(it=st.begin();it!=st.end();it++)
		{
			pa cur=*it; int y=cur.se;
			if(f[x][y]>k)
				st.erase(it),st.insert(mp(cur.fs-1,y));
		}
		for(int i=in[x];i;i=e[i].lt)
		{
			int y=e[i].to; d[y]--;// printf("%d %d\n",y,d[y]);
			if(d[y]==1)
			{
				tmp=0;
				for(int j=1;j<=n;j++)
					if(!del[j]&&f[y][j]>k)	tmp++;
				st.insert(mp(tmp,y));
			}
		}
		ans++;
	}
	printf("%d\n",ans);
}

int main()
{
	int x,y;
	scanf("%d%d",&n,&k);
	for(int i=1;i<n;i++)	scanf("%d%d",&x,&y),add(x,y),d[x]++,d[y]++;
	work();
	return 0;
}

D - Arrays and Palindrome

人太咸鱼 没有理想 然后就看题解了T^T

发现有两个以上长度是奇数的就是无解

如果以下的话就两边一边一个 然后一个+1 一个-1就好了 别的细节什么的看代码吧。

就是这个整个过程其实是利用两个串不停连边【连边即为相同】然后两个串分开的时候需要用另一个串连接起来 这个过程偶数是可以做到的但是奇数不行【中间的那个元素被空出来了】所以就是这个样子啦

看一下editorial比较好emm我说的不是很严谨。。。

代码。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define inf 20021225
#define ll long long
#define mxn 110
using namespace std;

int n,a[mxn],m;

int main()
{
	int cnt=0;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%d",&a[i]);
		cnt+=a[i]%2;
	}
	if(cnt>2)
	{
		printf("Impossible\n");
		return 0;
	}
	int fs=0;
	for(int i=1;i<=m;i++)
	{
		if(a[i]%2==1)
		{
			if(!fs)	swap(a[1],a[i]),fs=1;
			else	swap(a[m],a[i]);
		}
	}
	for(int i=1;i<=m;i++)	printf("%d ",a[i]);puts("");
	if(m==1)
	{
		if(a[1]==1)	printf("1\n1\n");
		else	printf("2\n1 %d\n",a[1]-1);
		return 0;
	}
	a[1]--; a[m]++;
	if(a[1]==0)
	{
		printf("%d\n",m-1);
		for(int i=2;i<=m;i++)	printf("%d ",a[i]);
	}
	else
	{
		printf("%d\n",m);
		for(int i=1;i<=m;i++)	printf("%d ",a[i]);
	}
	return 0;
}

E - BBQ Hard

组合计数= = 戳到软肋了 不过刷agc就是为了练这个的emm

推一下柿子 大概是这个样子的

然后我们观察到 a和b都比较小 但是n比较大所以我们可以转成Lattice path问题

然后就不会做了= =

这个题需要把柿子转换一下 大概长这个样子

就是直接全计数然后去不合法去重

观察到 后面那个柿子直接O(1)算就行了

然后前面这个是典型的Lattice Path问题

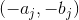
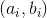
表示从走到的路径

然后扔图上dp一下就行了qwq

计数好题要码一下= =+

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define inf 20021225
#define ll long long
#define mdn 1000000007
using namespace std;

int f[4100][4100],inv2;
int fac[8100],inv[8100];
int n,a[200010],b[200010];

int ksm(int bs,int mi)
{
	int ans=1;
	while(mi)
	{
		if(mi&1)	ans=(ll)ans*bs%mdn;
		bs=(ll)bs*bs%mdn; mi>>=1;
	}
	return ans;
}

int C(int x,int y)
{
	if(x<y)	return 0;
	return (ll) fac[x] * inv[x-y] %mdn *inv[y]%mdn;
}
bool vis[4100][4100];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)	scanf("%d%d",&a[i],&b[i]),f[2001-a[i]][2001-b[i]]+=1;
	fac[0]=inv[0]=1; inv2=ksm(2,mdn-2);
	for(int i=1;i<=8001;i++)	fac[i]=(ll)fac[i-1]*i%mdn;
	inv[8001]=ksm(fac[8001],mdn-2);
	for(int i=8000;i;i--)	inv[i]=(ll)inv[i+1]*(i+1)%mdn;
	for(int i=1;i<=4001;i++)
		for(int j=1;j<=4001;j++)
			f[i][j]+=f[i-1][j]+f[i][j-1],f[i][j]%=mdn;
	int mns=0,add=0;
	for(int i=1;i<=n;i++)
		mns = ((ll)mns + C(2*(a[i]+b[i]),2*a[i]))%mdn , add = ((ll)add + f[2001+a[i]][2001+b[i]])%mdn;
	//printf("%d %d %d\n",a[i],b[i],f[2001+a[i]][2001+b[i]]);
	add -= mns; if(add<0)	add+=mdn;
	//printf("%d\n",mns);
	printf("%d\n",(ll)add*inv2%mdn);
	return 0;
}

AGC001打卡(2018-12-27)