C语言实现二叉树

二叉树的重要性就不用多说啦；

我以前也学习过，但是一直没有总结；

网上找到的例子，要么是理论一大堆，然后是伪代码实现；

要么是复杂的代码，没有什么解释；

最终，还是靠翻墙找到一些好的文章，参考地址我会在See Also部分给大家贴出来

Problem

假设我们要生成的二叉树如下图；

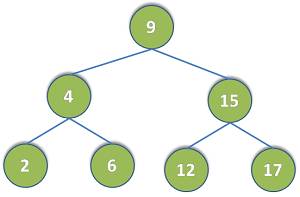
Solution

显然，我们需要在节点保存的数据只有一个整数；

struct binary_tree {
    int data    ;   // Data area
    //TODO
};

所以在结构体里面，我们的代码应该类似上面的写法；

通过观察我们还发现，每一个节点都指向左右两边（除了最后的叶子节点外）；

因此，我们需要让它有两个指针域；

可能你会想到类似如下的写法；

struct binary_tree {
    int data    ;   // Data area
    void * left;
    void * right;
}; 

上面的定义格式似乎是正确的，但是类型好像并不是我们想要的；

例如：当left指向左边的子节点时，子节点应该也是一个包涵数据域的节点；

因此我们需要再定义一个与它本身相同的结构体；

struct binary_tree {
    int data    ;   // Data area
    struct binary_tree * left;
    struct binary_tree * right;
};

所以，我们会这样去定义它；

显然，这是一个递归定义；

如果我们要实例化一个节点，我们可以:

struct binary_tree * tree;

显然我们需要定义一个实例写那么长的类型名字，实在让人难受；

因此，我们可以这样；

typedef struct binary_tree node;
node * tree;

好啦！到此为止我们的数据域就定义好啦！你现在的代码应该是下面的样子啦；

struct binary_tree {
    int data    ;   // Data area
    binary_tree * left;
    binary_tree * right;
};  

typedef struct binary_tree node;

接下来我们需要把数据插入到对应的位置上；

我们希望树左边分支的的数据总是比树右边分支的要小；

至于为什么我们暂时不解释；

void insert(node ** tree, int val) {
    node * temp = NULL;
    if(!(*tree)) {
        //TODO
        return ;
    }

    if (val < (*tree)->data) {
        //TODO
    }else if (val > (*tree)->data) {
        //TODO
    }
}

因此我们代码会像上面这样写；

第一个if语句判断这个树节点是否存在；

若是不存在，我们应该生成一个节点，然后添加到树上来；

第二个if-else呢，则是判断这个给定要存入的数据是大于当前节点的呢还是小于；

小于呢，存在左分支。大于存在右分支；

    if(!(*tree)) {
        temp = (node *)malloc(sizeof(node));
        temp->left = temp->right = NULL;
        temp->data = val;
        *tree = temp;
        return ;
    }
    

分析上面代码片段，我们发现temp的作用是临时变量正如其名；

malloc分配内存，然后初始化节点左右指针域为空，以及数据域为val；

最后*tree=temp 把节点安装到树上；

并且返回上一级；

对于已经存在的树节点，我们需要往左右两分子扩展；

因此我们的代码会是这样的；

 if (val < (*tree)->data) {
        insert(&(*tree)->left,val);
  }else if (val > (*tree)->data) {
        insert(&(*tree)->right,val);
  }

从代码中可以看出，只对小于和大于两个方向的数据进行操作；

你也许会考虑到万一等于呢。

注意，在这里应该是数据的唯一性有要求的，它类似于数学里的集合，不会有重复的；

它的这种特性对我们往后要写得单词统计程序非常有帮助；

那么这个函数的所有代码如下：

void insert(node ** tree, int val) {
    node * temp = NULL;
    if(!(*tree)) {
        temp = (node *)malloc(sizeof(node));
        temp->left = temp->right = NULL;
        temp->data = val;
        *tree = temp;
        return ;
    }

    if (val < (*tree)->data) {
        insert(&(*tree)->left,val);
    }else if (val > (*tree)->data) {
        insert(&(*tree)->right,val);
    }
}

节点创建好了，注意我们用malloc创建；

因此，我们是在堆中分配的内存，因此我们需要手动释放；

那显然需要用到free函数与之对应；

所以我们释放节点的函数应该是这样的；

void deltree(node * tree) {
    if(tree) {
        free(tree);
    }
}  

这样似乎也没有问题啦！但是仔细观察我们发现；

直接释放啦free就只是释放啦根节点；

就好比，我们去拔花生；我们只是简单的用剪刀把上面的叶子剪断啦；

没有想过把花生沿着根一直挖下去是不可能把所有花生弄出来的；

因此，我们需要这样做；

void deltree(node * tree) {
    if(tree) {
        deltree(tree->left);
        deltree(tree->right);
        free(tree);
    }
}

这样我们找到左边的根啦，又继续往左边找；

找不到啦，就往右边找；

再找不到啦，就执行到free释放节点然后返回上一级；

好啦！树也有函数建啦，也有办法“砍”啦！

接下来是怎么展示我们的树啦；

树的遍历有三种；

前，中，后；

void print_preorder(node * tree) {
    if(tree) {
        //TODO

    }
}  

首先我们需要判断tree是否空；

要是空的，我们就没有必要看里面还有什么数据啦；

void print_preorder(node * tree) {
    if(tree) {
        printf("%d\n",tree->data);
        print_preorder(tree->left);
        print_preorder(tree->right);
    }
}

同样的我们把中序和后序写出来；

void print_preorder(node * tree) {
    if(tree) {
        printf("%d\n",tree->data);
        print_preorder(tree->left);
        print_preorder(tree->right);
    }
}

void print_inorder(node * tree) {
    if(tree) {
        print_inorder(tree->left);
        printf("%d\n",tree->data);
        print_inorder(tree->right);
    }
}

void print_postorder(node * tree) {
    if(tree) {
        print_postorder(tree->left);
        print_postorder(tree->right);
        printf("%d\n",tree->data);
    }
}

好啦！该有的函数都有啦；

我们该写测试函数啦；

int main(void)
{
    node * root;
    node * tmp;
    //int i;

    root = NULL;
    /* Inserting nodes into tree */
    insert(&root,);
    insert(&root,);
    insert(&root,);
    insert(&root,);
    insert(&root,);
    insert(&root,);
    insert(&root,);

    printf("Pre Order Display\n");
    print_preorder(root);

    printf("In Order Display\n");
    print_inorder(root);

    printf("Post Order Display\n");
    print_postorder(root);

    /* Deleting all nodes of tree */
    deltree(root);
}

运行结果如下：

Pre Order Display

In Order Display

Post Order Display

Discussion

然后这个例子似乎太简单了！它没有对树进行查询的函数；

也没有树的高度进行测量；

但是，它的简洁是为了更加容易理解；

可是呢！太简洁了，以至于我们都不知道为什么要把数据弄成树形结构；

为什么，难道线性结构的数据还不能解决我们身边的问题吗？

这个问题，不知道大家有没有问过自己。反正我以前经常问自己；

那么，为了让大家理解存在树形结构的数据的必要性；

我们，设想要统计C语言的关键字在代码中出现的频率；

我们会怎么做呢？？（这个问题我会在另一篇文章讲解）

See Alson

http://www.thegeekstuff.com/2013/02/c-binary-tree/