[LeetCode] 由 “找零钱" 所想

Ref: [Optimization] Dynamic programming【寻找子问题】

Ref: [Optimization] Advanced Dynamic programming【优于recursion】

显然，本篇是关于”动态规划"的部分。

---

找零钱

一、简单直白策略

要点：”个数“其实代表了“for循环”的层数。但“个数”不定，使用“递归”反而能解决这个问题，减少思路上的负担。

import time 

def recMC(coinValueList, change):
    minCoins = change
    if change in coinValueList:
        return 1
    else:
        for i in [c for c in coinValueList if c <= change]:
            # 遍历每一个变量, 相当于多重循环。有意思的是，循环的深度是不确定的;
            numCoins = 1 + recMC(coinValueList, change-i)
            # 得到这个遍历分支的最终结果；
            if numCoins < minCoins:
                minCoins = numCoins
    return minCoins

start = time.time()
print(recMC([1,5,10,25], 63))
end = time.time()
print(end-start)

耗时：31秒。

二、记忆化策略

要点：增加了”结果缓存“，效率极具增加。

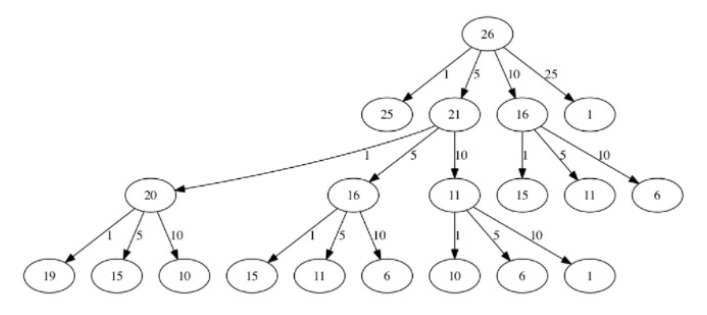
代码中的 knownResults 记录了上图中节点（某个change时）的最优/最小的值，作为了记录。

def recDC(coinValueList, change, knownResults):
    minCoins = change
    if change in coinValueList:
        knownResults[change] = 1　　# 一个硬币刚刚好
        return 1
    elif knownResults[change] > 0:
return knownResults[change]
    else:
        for i in [c for c in coinValueList if c <= change]:
            #
            numCoins = 1 + recDC(coinValueList, change-i, knownResults)
            # 更新minCoins
            if numCoins < minCoins:
                minCoins = numCoins
                knownResults[change] = minCoins

    return minCoins

def main():
    amnt = 2163
    print(recDC([1,2,5,10,21,25], amnt, [0]*(amnt+1)))

main()

耗时：0.01秒。

三、动态规划策略

　　要点：不是从上到下的 (递归) 思维，且容易栈溢出；而是从最小的情况入手，逐渐扩大。

def dpMakeChange(coinValueList, change, minCoins, coinsUsed):
    # 首先，考虑所有的 "情况"，是从小到大考虑
    for cents in range(change+1):

        coinCount = cents
        newCoin = 1

        # 考虑这些 "情况" 下的可行的 "硬币"
        for j in [c for c in coinValueList if c <= cents]:
            # 拿掉这枚"硬币"，考虑 "上一个问题"的最优值
            if minCoins[cents-j] + 1 < coinCount:
                coinCount = minCoins[cents-j] + 1
                newCoin = j

        # 考虑过该 "情况"，更新记录
        minCoins[cents]  = coinCount
        coinsUsed[cents] = newCoin

    return minCoins[change]

def printCoins(coinsUsed, change):
    coin = change
    while coin > 0:
        thisCoin = coinsUsed[coin]
        print(thisCoin)
        coin = coin - thisCoin

@fn_timer
def main():
    amnt = 2163
    clist = [1,2,5,10,21,25]
    coinsUsed = [0]*(amnt+1)
    coinsCount = [0]*(amnt+1)

    # print("Making change for", amnt, "requires")
    print(dpMakeChange(clist, amnt, coinsCount, coinsUsed), "coins")
    # print("They are:")
    # printCoins(coinsUsed,amnt)
    # print("The used list is as follows:")
    # print(coinsUsed)

main()

耗时：0.003秒。

End.