决策树（基于增益率）之python实现

如图，为使用到的公式，信息熵表明样本的混乱程度，增益表示熵减少了，即样本开始分类，增益率是为了平衡增益准则对可取值较多的属性的偏好，同时增益率带来了对可取值偏小的属性的偏好，实际中，先用增益进行筛选，选取大于增益平均值的，然后再选取其中增益率最高的。

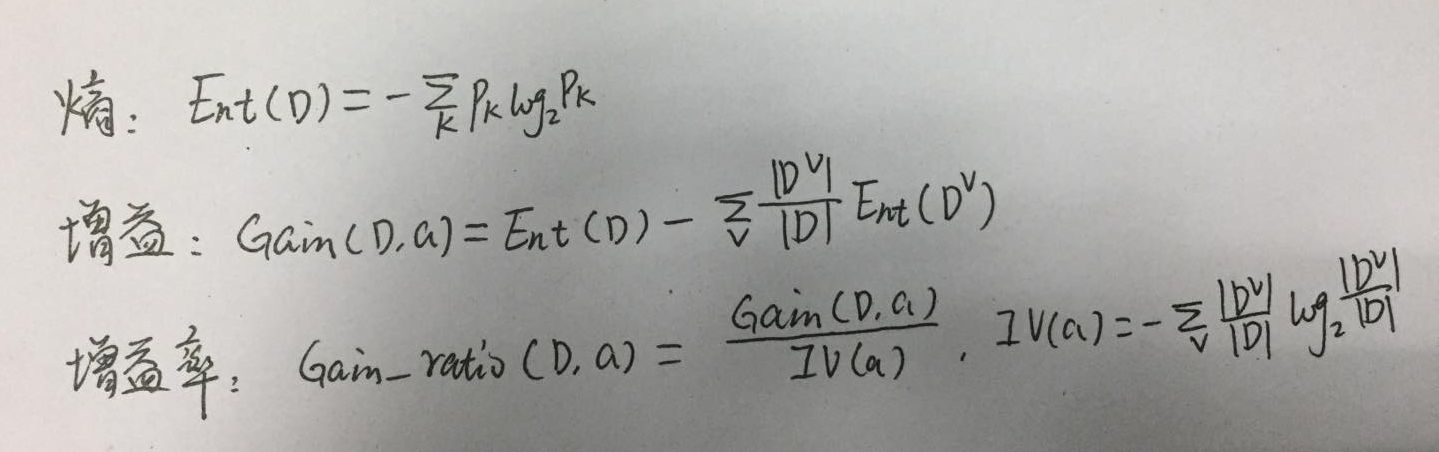
以下代码纯粹手写，未参考其他人代码，如果问题，请不吝赐教。

1，计算信息熵的函数

import numpy as np
# 计算信息熵
# data:like np.array
# data.shape=(num_data,data_features+1) 即属性与label放一起了
def entropy(data,num_class):
    class_set=list(set(data[:,-1]))
    result=0
    length=len(data)
#     这里修改一下，不使用num_class
    for i in range(len(class_set)):
        l=len(data[data[:,-1]==class_set[i]])
        p=l/length
        result-=p*np.log2(p)
    return result

2，计算增益及属性a的固有值（IV）

# 计算不同属性的信息增益
# detail_features：特征构成的list，每个特征的可取值构成list元素，即也是list
def calculate_gain(data,detail_features,num_class):
　　'''返回各属性对应的信息增益及平均值'''
    result=[]
    ent_data=entropy(data,num_class)
    for i in range(len(detail_features)):
        res=ent_data
        for j in range(len(detail_features[i])):
            part_data=data[data[:,i]==detail_features[i][j]]
            length=len(part_data)
            res-=length*entropy(part_data,num_class)/len(data)
        result.append(res)
    return result,np.array(result).mean()
# 计算某个属性的固有值
def IVa(data,attr_index):
    attr_values=list(set(data[:,attr_index]))
    v=len(attr_values)
    res=0
    for i in range(v):
        part_data=data[data[:,attr_index]==attr_values[i]]
        p=len(part_data)/len(data)
        res-=p*np.log2(p)
    return res    

3，构建节点类，以便构建树

class Node:
    def __init__(self,key,childs):
        self.childs=[]
        self.key=key
    def add_node(self,node):
        self.childs.append(node)

4，构建树

# 判断数据是否在所有属性的取值都一样，以致无法划分
def same_data(data,attrs):
    for i in range(len(attrs)):
        if len(set(data[:,i]))>1:
            return False
    return True

# attrs:属性的具体形式
def create_tree(data,attrs,num_class,root):
#     注意这里3个退出条件
    #     1，如果数据为空，不能划分，此时这个叶节点不知标记为哪个分类了
    if len(data)==0:
        return
#   2，如果属性集为空，或所有样本在所有属性的取值相同，无法划分，返回样本最多的类别
    if len(attrs)==0 or same_data(data,attrs):
        class_set=list(set(data[:,-1]))
        max_len=0
        index=0
        for i in range(len(class_set)):
            if len(data[data[:,-1]==class_set[i]])>max_len:
                max_len=len(data[data[:,-1]==class_set[i]])
                index=i
        root.key=root.key+class_set[index]
        return
#     3，如果当前节点包含同一类的样本，无需划分
    if len(set(data[:,-1]))==1:
        root.key=root.key+data[0,-1]
        return
    ent=entropy(data,num_class)
    gain_result,mean=calculate_gain(data,attrs,num_class)
    max=0
    max_index=-1
#     求增益率最大
    for i in range(len(gain_result)):
        if gain_result[i]>=mean:
            iva=IVa(data,i)
            if gain_result[i]/iva>max:
                max=gain_result[i]/iva
                max_index=i
    for j in range(len(attrs[max_index])):
        part_data=data[data[:,max_index]==attrs[max_index][j]]
#         删除该列特征
        part_data=np.delete(part_data,max_index,axis=1)
#         添加节点
        root.add_node(Node(key=attrs[max_index][j],childs=[]))
#         删除某一类已判断属性
        new_attrs=attrs[0:max_index]
        new_attrs.extend(attrs[max_index+1:])
        create_tree(part_data,new_attrs,num_class,root.childs[j])        

5，使用西瓜数据集2.0测试，数据这里就手写了，比较少

def createDataSet():
    """
    创建测试的数据集
    :return:
    """
    dataSet = [
        #
        ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        #
        ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        #
        ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        #
        ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
        #
        ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
        #
        ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
        #
        ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
        #
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],

        # ----------------------------------------------------
        #
        ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
        #
        ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
        #
        ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],
        #
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
        #
        ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
        #
        ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
        #
        ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
        #
        ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],
        #
        ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']
    ]

    # 特征值列表
    labels = ['色泽', '根蒂', '敲击', '纹理', '脐部', '触感']

    # 特征对应的所有可能的情况
    labels_full = []

    for i in range(len(labels)):
        items=[item[i] for item in dataSet]
        uniqueLabel = set(items)
        labels_full.append(list(uniqueLabel))
    return np.array(dataSet), labels, labels_full

6，开始构建树

dataset,labels,labels_full=createDataSet()

root=Node('',[])
create_tree(dataset, labels_full, 2, root)

7，打印树结构

def print_root(n,root):print(n,root.key)
    for node in root.childs:
        print_root(n+1,node)
print_root(0,root)      

打印结果为：数字表示层次

0
1 模糊坏瓜
1 稍糊
2 硬滑坏瓜
2 软粘好瓜
1 清晰
2 硬滑好瓜
2 软粘
3 青绿
4 稍蜷好瓜
4 蜷缩
4 硬挺坏瓜
3 乌黑坏瓜
3 浅白

8，绘制树形结构，这里我就手动绘制了。图中有2个叶节点为空白，即模型不知道该推测其为好瓜还是坏瓜。这里我暂时没有好的思路解决，只能随机处理？

9，总结

首先，暂时没有添加predict函数。其次，这是个简陋版的实现，有很多待优化的地方，如连续值处理、缺失值处理、剪枝防止过拟合，树的创建使用的是递归（样本大导致栈溢出，改成队列实现较好），也有基于基尼指数的实现，还有多变量决策树（可实现复杂的分类边界）。