编译原理 算法3.8 LR分析 c++11实现

LR分析简介

　　LR分析是应用最广泛的一类分析方法，它是实用的编译器功能中最强的分析器，其特点是:

　　1，采用最一般的无回溯移进-规约方法。

　　2，可分析的文法是LL文法的真超集。

　　3，能够及时发现错误，及时从左扫描输入序列的最大可能。

　　4，分析表较为复杂，难以手工构造。

实验内容

　　根据LR分析表action和goto实现LR分析。

实验步骤

　　输入 序列$\omega$和文法$G$的LR分析表action与goto。

　　输出 若$\omega \in L(G)$，得到$\omega$的规范规约，否则指出一个错误。

具体实现

　　见代码。

 #include <algorithm>
 #include <fstream>
 #include <iostream>
 #include <map>
 #include <set>
 #include <stack>
 #include <vector>
 using namespace std;

 using Production = pair<string, vector<string>>;

 const int max_state = ;
 const int delay_num = 5e8;

 struct ParserLR
 {

     map<string, int> mp_n; //非终结符映射
     map<string, int> mp_t; //终结符映射
     vector<Production> P;  //产生式
     vector<string> N, T;   //非终结符，终结符
     int state_num, operator_num, nonterminal_num, terminal_num, production_num;
     vector<string> action[max_state];
     vector<int> _goto[max_state];
     int init(string filename)
     {
         N.clear();
         T.clear();
         P.clear();
         mp_n.clear();
         mp_t.clear();
         for (int i = ; i < max_state; i++)
         {
             action[i].clear();
             _goto[i].clear();
         }
         state_num = operator_num = nonterminal_num = terminal_num = production_num = ;
         ifstream in(filename, ios::in);
         if (!in.is_open())
             return ;
         in >> terminal_num;
         for (int i = ; i < terminal_num; i++)
         {
             string tmp;
             in >> tmp;
             T.emplace_back(tmp);
             mp_t[tmp] = i;
         }
         in >> nonterminal_num;
         for (int i = ; i < nonterminal_num; i++)
         {
             string tmp;
             in >> tmp;
             N.emplace_back(tmp);
             mp_n[tmp] = i;
         }
         in >> production_num;
         for (int i = ; i < production_num; i++)
         {
             Production cur;
             in >> cur.first;
             int sz;
             in >> sz;
             for (int j = ; j < sz; j++)
             {
                 string t;
                 in >> t;
                 cur.second.emplace_back(t);
             }
             P.emplace_back(cur);
         }
         in >> state_num;
         for (int i = ; i <= state_num; i++)
             for (int j = ; j < terminal_num; j++)
             {
                 string tmp;
                 in >> tmp;
                 action[i].emplace_back(tmp);
             }
         for (int i = ; i <= state_num; i++)
             for (int j = ; j < nonterminal_num; j++)
             {
                 int tmp;
                 in >> tmp;
                 _goto[i].emplace_back(tmp);
             }
         return ;
     }
     Production getProduction(int idx)
     {
         return P[idx - ];
     }
     pair<int, vector<Production>> analyze(vector<string> input) //first->出错位置，-1代表无错
     {
         vector<Production> error;
         vector<Production> success;
         stack<string> ch; //符号栈
         stack<int> st;    //状态栈
         ch.emplace("#");
         st.emplace();
         input.emplace_back("#");
         int sz = input.size();
         for (int i = ; i < sz;)
         {
             string now = input[i];
             if (!mp_t.count(now))
                 return make_pair(i, success);
             int ip = mp_t[now];
             int top = st.top(); //栈顶状态
             string at = action[top][ip];
             if (at[] == 'r') //规约
             {
                 string res = at.substr(, at.size());
                 int num = stoi(res);
                 Production trans = getProduction(num);
                 for (int i = ; i < trans.second.size(); i++)
                 {
                     st.pop();
                     ch.pop();
                 }
                 top = st.top();
                 string cur = trans.first;
                 ch.emplace(cur);
                 st.emplace(_goto[top][mp_n[cur]]);
                 success.emplace_back(trans);
             }
             else if (at[] == 's') //移进
             {
                 string res = at.substr(, at.size());
                 int to_state = stoi(res);
                 st.emplace(to_state);
                 ch.emplace(now);
                 i++;
             }
             else if (at == "acc") //接受
                 return make_pair(-, success);
             else //error
             {
                 if (now == "#")
                     return make_pair(i - , success);
                 return make_pair(i, success);
             }
         }
         return make_pair(, error);
     }
 };
 inline void delay()
 {
     for (int i = ; i < delay_num; i++)
         ;
 }
 inline void display(const pair<int, vector<Production>> &out)
 {
     if (out.first == -)
     {
         for (int i = ; i < out.second.size(); i++)
         {
             cout << out.second[i].first << "->";
             for (int j = ; j < out.second[i].second.size(); j++)
                 cout << out.second[i].second[j];
             cout << "\n";
         }
     }
     else
         cout << "在第" << out.first +  << "个终结符出错.\n";
 }
 int main(int argc, char const *argv[])
 {
     ParserLR app;
     string filename = "prj3_8_in.txt";
     if (app.init(filename))
     {

         cout << "构建分析器中";
         delay();
         cout << ".";
         delay();
         cout << ".";
         delay();
         cout << ".\n";
         delay();
         cout << "构建成功.\n";
         cout << "请输入终结符个数:";
         int sz;
         cin >> sz;
         cout << "请输入包含" << sz << "个终结符的待分析序列, 终结符间需用空格分离:";
         vector<string> al;
         for (int i = ; i < sz; i++)
         {
             string tmp;
             cin >> tmp;
             al.emplace_back(tmp);
         }
         cout << "开始分析";
         delay();
         cout << ".";
         delay();
         cout << ".";
         delay();
         cout << ".\n";
         delay();
         cout << "分析结束.\n";
         pair<int, vector<Production>> out = app.analyze(al);
         cout << "分析成功,结果如下:\n";
         display(out);
     }
     return ;
 }

源代码

id - * #

E T F

E  E - T
E  T
T  T * F
T  F
F  - F
F  id

s4 s5 null null
null s6 null acc
null r2 s7 r2
null r4 r4 r4
null r6 r6 r6
s4 s5 null null
s4 s5 null null
s4 s5 null null
null r5 r5 r5
null r1 s7 r1
null r3 r3 r3

- - -
- - -
- - -
- - -
- -
-
- -
- - -
- - -
- - -

输入文件

效果展示

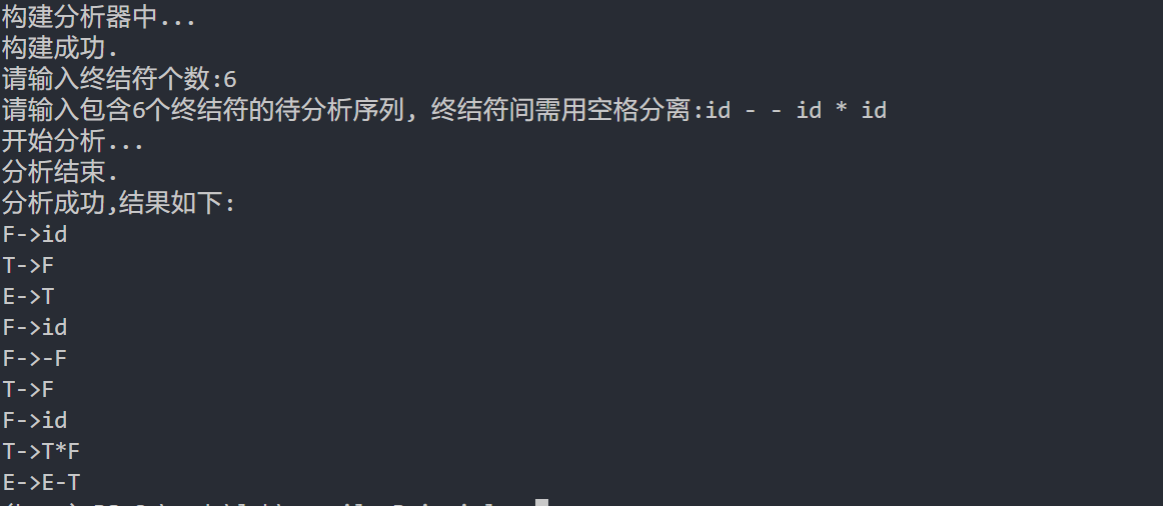
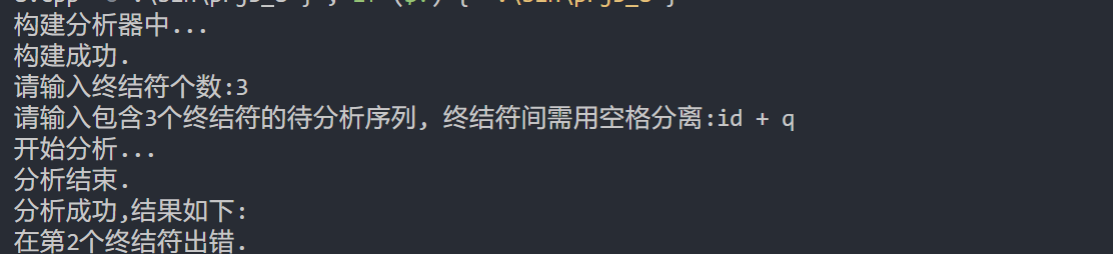
代码使用部分c++11特性，如有本地编译需要，请确认环境。

欢迎下方留言。