I-string_2019牛客暑期多校训练营（第四场）

题意

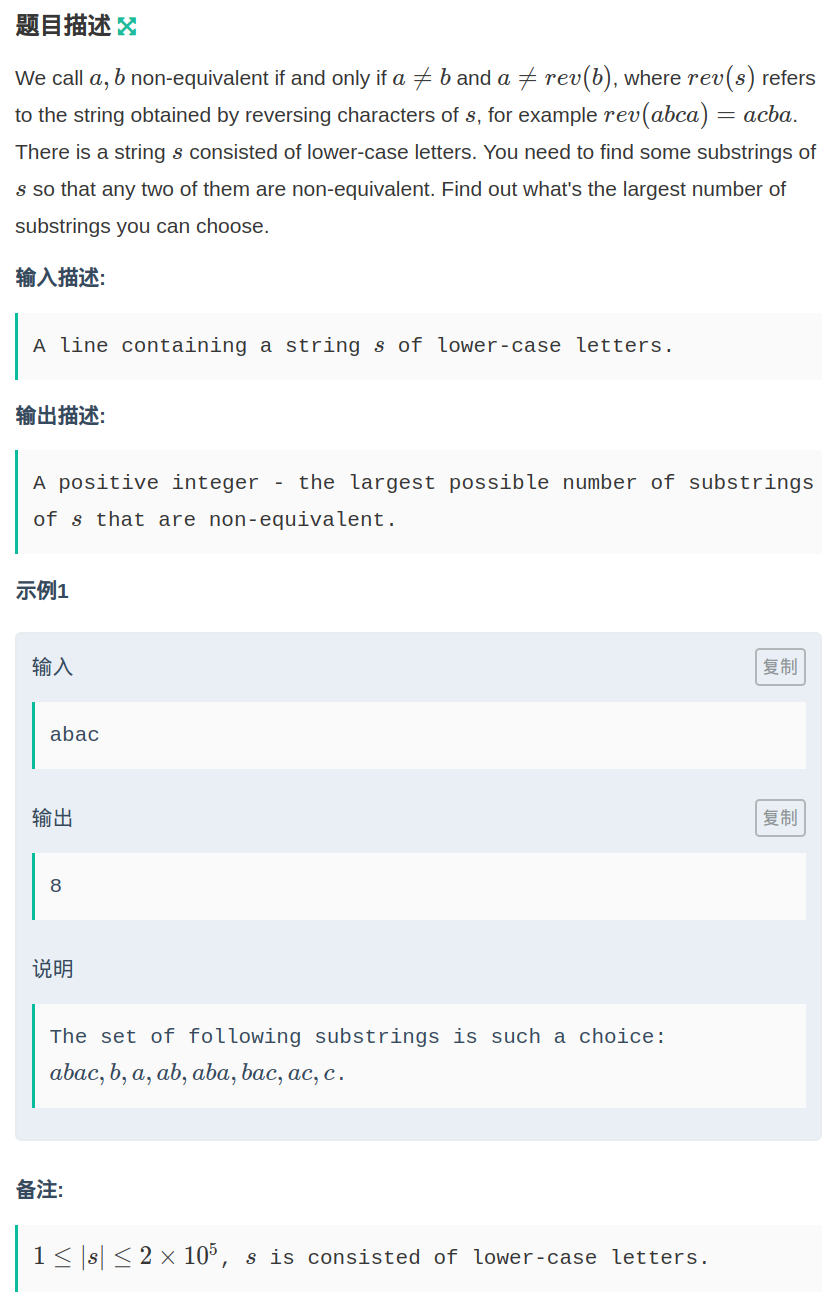
当a != b且a != rev(b)则认为a串与b串不相等，rev(b)表示b串的反串，例如rev(abcd) = dcba

给出一个串求出该串所有不相等的子串个数

题解

先利用后缀数组求出s#rev(s)的不相等子串个数，再扣掉包含字符‘#’的子串个数，包含‘#’的子串个数为\((len(s)+1)^2\),具体取法为以#及左边任意字符为起点，以#及右边字符为终点构成的串，显然这样能取出所有包含#的子串，且这些子串都不相等。

所以求出来结果是\(ans = \frac{(2len(s)+1)*(2len(s))}{2}- \sum_{i=2}^{2len(s)+1}height[i]-(len(s)+1)^2\), 这样求出来的结果是包含a = rev(b)的，比如s = abac，求出来的结果是\({a,b,c,ab,ba,ac,ca,cab,aba,bac,abac,caba}\),可以看出来除了\({a,b,c,aba}\)这几个回文串，剩余的串都是成对的，那么我们用回文树求出s本质不同的回文串个数加上之前的ans再除以2就是答案了

代码

#include <bits/stdc++.h>

const int mx = 5e5+5;
typedef long long ll;
char str[mx];

int t1[mx], t2[mx], c[mx];
int sa[mx], rank[mx], height[mx];

bool cmp(int *r, int a, int b, int l) {
    return r[a] == r[b] && r[a+l] == r[b+l];
}

void da(int n, int m) {
    n++;
    int i, j, p, *x = t1, *y = t2;
    for (i = 0; i < m; i++) c[i] = 0;
    for (i = 0; i < n; i++) c[x[i] = str[i]]++;
    for (i = 1; i < m; i++) c[i] += c[i-1];
    for (i = n-1; i >= 0; i--) sa[--c[x[i]]] = i;
    for (j = 1; j <= n; j <<= 1) {
        p = 0;
        for (i = n-j; i < n; i++) y[p++] = i;
        for (i = 0; i < n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;
        for (i = 0; i < m; i++) c[i] = 0;
        for (i = 0; i < n; i++) c[x[y[i]]]++;
        for (i = 1; i < m; i++) c[i] += c[i-1];
        for (i = n-1; i >= 0; i--) sa[--c[x[y[i]]]] = y[i];

        std::swap(x, y);
        p = 1; x[sa[0]] = 0;
        for (i = 1; i < n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p-1 : p++;
        if (p >= n) break;
        m = p;
    }
    int k = 0;
    n--;
    for (i = 0; i <= n; i++) rank[sa[i]] = i;
    for (i = 0; i < n; i++) {
        if (k) k--;
        j = sa[rank[i]-1];
        while (str[i+k] == str[j+k]) k++;
        height[rank[i]] = k;
    }
}

const int N = 26;
struct pTree {
    int Next[mx][N];
    int fail[mx];
    ll cnt[mx];
    ll sum[mx];
    int num[mx];
    int len[mx];
    int S[mx];
    int last, n, p, cur, now;

    int newnode(int l) {
        for (int i = 0; i < N; i++) Next[p][i] = 0;
        cnt[p] = num[p] = 0;
        len[p] = l;
        return p++;
    }

    void init() {
        n = p = 0;
        newnode(0);
        newnode(-1);
        last = 0;
        S[n] = -1;
        fail[0] = 1;
    }

    int getFail(int x) {
        while (S[n - len[x] - 1] != S[n]) x = fail[x];
        return x;
    }

    bool add(int c) {
        S[++n] = c;
        cur = getFail(last);
        bool flag = false;
        if (!Next[cur][c]) {
            flag = true;
            now = newnode(len[cur] + 2);
            fail[now] = Next[getFail(fail[cur])][c];
            Next[cur][c] = now;
            num[now] = num[fail[now]] + 1;
        }
        last = Next[cur][c];
        cnt[last]++;
        return flag;
    }
    void count() {
        for (int i = p-1; i >= 0; i--) cnt[fail[i]] += cnt[i];
    }
}tree;

int main() {
    scanf("%s", str);
    int len = std::strlen(str);
    str[len] = '#';
    for (int i = len+1; i <= 2*len; i++) str[i] = str[2*len-i];
    str[2*len+1] = '\0';

    int n = 2*len+1;
    da(n, 128);
    ll tot = 1LL * (2*len+1) * (2*len+2)/2;
    tot -= 1LL * (len+1) * (len+1);
    for (int i = 2; i <= n; i++) tot -= height[i];

    tree.init();
    for (int i = 0; i < len; i++) tree.add(str[i]-'a');
    printf("%lld\n", (tot+tree.p-2)/2);
    return 0;
}