P8340 [AHOI2022] 山河重整

\(20pts\) 给 \(O(2^n)\) 枚举，\(60pts\) 是 \(O(n^2)\)，先看看怎么做。计数题无非容斥和 \(dp\)，不妨从 \(dp\) 入手。多项式复杂度的做法意味着无法将 \([1,n]\) 中是否能全部被表示直接存入状态，考虑将其转化为另一个充要条件，注意到：

• \(\forall i\in [1,n]\)，需要满足 \(S\) 中 \(\le i\) 的元素之和 \(\ge i\)。

证明：必要性显然，考虑使用数学归纳法证明其必要性。\(i=1,2\) 时显然，对于 \(i \ge 3\)，假设找到最小的 \(x\) 使得 \(\le x\) 的值相加的和 \(\ge i\)，设这个和为 \(s\)，则有 \(s \lt 2i\)（否则由于 \(x \le i\) 则 \(x\) 不是最小），而又有 \(i \le s\)，所以 \(s - i \lt i\)，由于 \(\lt i\) 的可以被表示，所以 \(\gt s - i\) 的也可以，即 \(\ge i\) 的可以被表示，证毕。

于是进行 \(O(n^2)\) 的背包 \(dp\)，可以获得 \(60pts\)，具体做法不再赘述。

然而这个状态不太好优化。思考完 \(dp\)，来考虑容斥（正难则反），即考虑不合法的情况有多少种。显然可以找到最小的 \(x\) 使得 \(S\) 中 \(\le x\) 的元素之和 \(\lt x\)，将其方案数从总和内减去。又发现，若 \(\le x\) 的元素之和 \(\lt x\) 且 \(x\) 最小，则 \(\le x-1\) 的元素之和必定 \(=x-1\)。如此一来，不妨设 \(f_i\) 为 \(\le i\) 的元素之和为 \(i\) 并且任意 \(x \le i\) 都合法的方案数，状态数量被优化为线性。

那么，问题转化为如何快速求出 \(f_i\)，同样可以容斥，用总方案数减去不合法的情况。总方案数就是 \(i\) 的整数拆分方案数，这个后面会讲。而不合法的方案数就是全局不合法方案的一部分，可以通过 \(f_{1\cdots i-1}\) 计算出。

现在考虑对一个数 \(n\) 进行整数拆分的方案数，一个 trivial 的想法是使用 \(O(n^2)\) 的背包。注意到背包的第二维值域为 \(n\)，而由于每次第二维要加上 \(i\)，使得增长速度很快，所以只会进行 \(\sqrt n\) 次第二维的增加操作，这给了我们优化的空间。

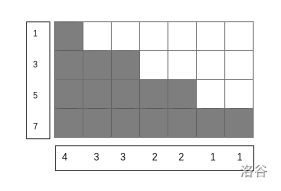
可以通过下图便于理解。行代表从小到大加入的不同的数，由于总方格数量为 \(n\)，所以行数是 \(O(\sqrt n)\) 级别的。但如果按照一行一行地做就不免要枚举第一维加入的 \(i\) 以及第二维的总和，复杂度是 \(O(n^2)\)。换一种思路，一列一列地做，相当于对 \([1,\sqrt{2n}] \cap \mathbb{Z}\) 做类似完全背包，并且为了保证每行互不相同，就需要让加入的数是连续的，只需要在 \(dp\) 时多留心一下，就得到了 \(O(n\sqrt n)\) 计算整数拆分的算法。

考虑前面的 \(f_j\) 对后面 \(f_i\) 的贡献，根据 \(f_j\) 的定义，一定有 \(j+1\) 没法被表示，所以 \(j+(j+2) \le i\)，同时要求 \([j+2,i]\cap S\) 的总和 \(s+j=i\)。类似于整数拆分，枚举新加入的列即可。如此一来，想要算出 \(f_i\) 就要求前面的 \(f_j\) 值已经确定。

考虑到 \(j \le \frac{i}{2}\)，可以通过类似于分治的方法，先计算出 \(f_{1\cdots n/2}\)，然后在 \(O(n \sqrt n)\) 的复杂度内贡献到 \(f_{n/2\cdots n}\) 中。总的时间复杂度为 \(T(n) = O(n \sqrt n) + T(n / 2) = O(n \sqrt n)\)。

代码如下：

int n, p, pw2[MAXN], f[MAXN], g[MAXN];
inline void add(int& x, int y) { x += y, x >= p && (x -= p); }
void solve(int n) {
    if (n <= 1) return void(f[0] = 1);
    solve(n >> 1);
    for (int i = 0; i <= n; ++i) g[i] = 0;
    for (int i = sqrt(n * 2); i >= 1; --i) {
        for (int j = n; j >= i; --j) g[j] = g[j - i];
        for (int j = 0; j + (j + 2) * i <= n; ++j) add(g[j + (j + 2) * i], f[j]);
        for (int j = i; j <= n; ++j) add(g[j], g[j - i]);
    }
    for (int i = n / 2 + 1; i <= n; ++i) if (g[i]) add(f[i], p - g[i]);
}
signed main() {
    read(n), read(p), pw2[0] = 1;
    for (int i = 1; i <= n; ++i) pw2[i] = 2ll * pw2[i - 1] % p;
    for (int i = sqrt(n * 2); i >= 1; --i) {
        for (int j = n; j >= i; --j) f[j] = f[j - i];
        add(f[i], 1);
        for (int j = i; j <= n; ++j) add(f[j], f[j - i]);
    }
    solve(n);
    int ans = pw2[n];
    for (int i = 0; i < n; ++i)
        add(ans, p - (ll)f[i] * pw2[n - i - 1] % p);
    write(ans), putchar('\n');
    return 0;
}