【算法题型总结】--6、BFS

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路

    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

1、反转二叉树

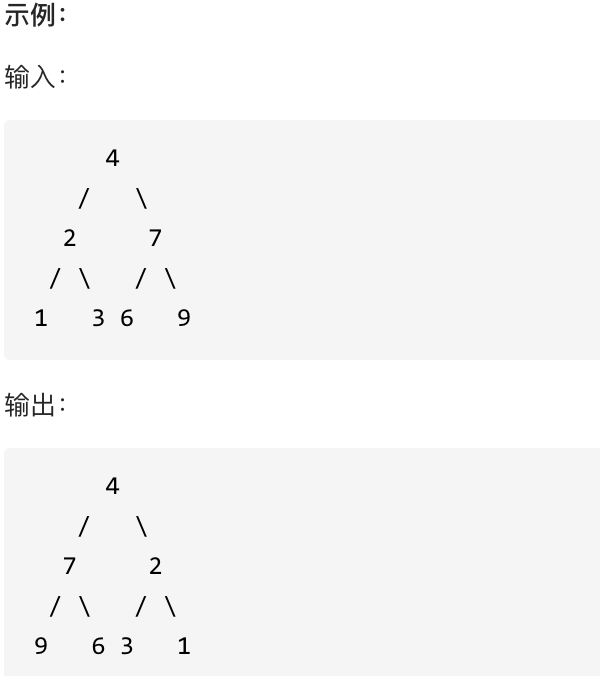
方法1：BFS

//BFS
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {return null;}
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            while (size-- > 0) {
                TreeNode node = deque.poll();
                swap(node);
                if (node.left != null) {deque.offer(node.left);}
                if (node.right != null) {deque.offer(node.right);}
            }
        }
        return root;
    }

    public void swap(TreeNode root) {
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
    }
}

其他方法

//DFS递归
class Solution {
   /**
     * 前后序遍历都可以
     * 中序不行，因为先左孩子交换孩子，再根交换孩子（做完后，右孩子已经变成了原来的左孩子），再右孩子交换孩子（此时其实是对原来的左孩子做交换）
     */
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        invertTree(root.left);
        invertTree(root.right);
        swapChildren(root);
        return root;
    }

    private void swapChildren(TreeNode root) {
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}