【读书笔记】组合计数中的行列式方法专题4 Routings: the Lindstrm–Gessel

书用的是Handbook of Enumerative Combinatorics (Miklos Bona)

专题4-Routings: the Lindstrm–Gessel–Viennot lemma

专题4-Routings: the Lindstrm–Gessel–Viennot lemma

一些定义

DAG 有向无环图
$\mathrm{wt}(e)$ 边的权重
$\mathrm{wt}(P)=\prod \mathrm {wt}(e)$ 路径的权重
$\mathrm{wt}(R)=\prod _{i=1}^n \mathrm {wt}(P)$ routing的权重
源，汇 Let S ={s1,...,sn} and T ={t1,...,tn} be two (not necessarily disjoint) sets of vertices,which we call sources and sinks,respectively
Routing定义 A routing from S to T is a set of paths P1,..., Pn from the n sources s1,...,sn to the n sinks t1,...,tn such that no two paths share a vertex.
Let π be the permutation of [n] such that $P_i$ starts at source $s_i$ and ends at sink $t_{π(i)}$, and deﬁne sign(R) = sign(π).
path matrix Q定义 $q_{ij}=\sum\limits_{P\ path from\ s_i to\ t_j }\mathrm{wt}(P)$ 考虑Q的元素$q_{ij}$时只是看$s_i$到$t_j$的所有路径

原文如下

the Lindstrm–Gessel–Viennot lemma

维基百科词条-Lindstrm–Gessel–Viennot lemma

式子右边的求和是对$S$到$T$的所有routings

【In particular】那里是说，

如果正好图还有这样的性质：每条边权都是1，而且$S$到$T$的所有routing都是1->1,2->2...这样的形式，那么$detQ=number \ of \ routings\ from\ S\ to \ T$

Lindstrm–Gessel–Viennot lemma 应用

Example1 Binomial determinants

$\begin{gathered}
\begin{pmatrix} a_1,...,a_n \\ b_1,...,b_n \end{pmatrix}
\end{gathered}$记号表示的是那个行列式

...开始我还看不懂为什么there are $\begin{gathered}
\begin{pmatrix} a_i \\ b_j \end{pmatrix}
\end{gathered}$ SE paths from $A_i$ to $B_j$

SE path 是说south 和 east ，我以为是往东往北了

since every SE routing from A to B takes Ai to Bi for all i, 这是因为0≤a1 <···<an and 0≤b1 <···<bn ; points A ={A1,...,An} and B ={B1,...,Bn} where Ai = (0,ai) and Bi = (bi,bi) for1≤i≤n 然后你还要要走SE path

Example2 Counting permutations by descent set

先定义一个n排列的decent set是说一个集合$S$，集合$S$的元素是index i使得$\pi_i>\pi_{i+1}$

然后问你 number of permutations of [n] with descent set$\{c_1,...,c_k\}$

可以构造一个A到B的SE routings构成bijeciton，答案是$\begin{gathered}
\begin{pmatrix} c_1,...c_k,n \\ 0,c_1,...,c_k \end{pmatrix}
\end{gathered}$(前面的行列式记号)

随手讲解图片里的例子，顺便讲一下符号

比如对于$\pi=27351684$(原书中给的是$\pi=28351674$，我认为应该是$\pi=27351684$，不然说不通)来说，

定义$\pi_i>\pi_{i+1}$的位置是$c_i$,$c_0$往往取$0$,$c_{k+1}$往往取$n$，这里$c=\{0,2,4,7,8\}$

定义了一个从permuation π到序列f的映射，$f_i$是满足$j\leq i \text { && } \pi_j\leq\pi_i $ 的 $j$ 的数量，这里，$f(\pi)=12231574$

接着在那些$c_i$位置处做分割，得到

$f(\pi)=12.23.157.4$

$B_i$点的坐标形如$(c_{i-1},c_{i-1})$，在y=x上

$A_i$点的坐标形如$(0,c_i)$

路径如何确定？拿到序列$f$被分割后的片段$f^i$，比如第一段是{1,2}，那么在$B_4$到$A_4$的2步长path中，第1步和第2步就是N step,其他步是W step

Example3 Rhombus tilings and plane partitions

让你用【1,1,1,1 60° 120°】的菱形密铺边长为$n$的正六边形(需要按照网格线摆放)。问你方案数$R_n$

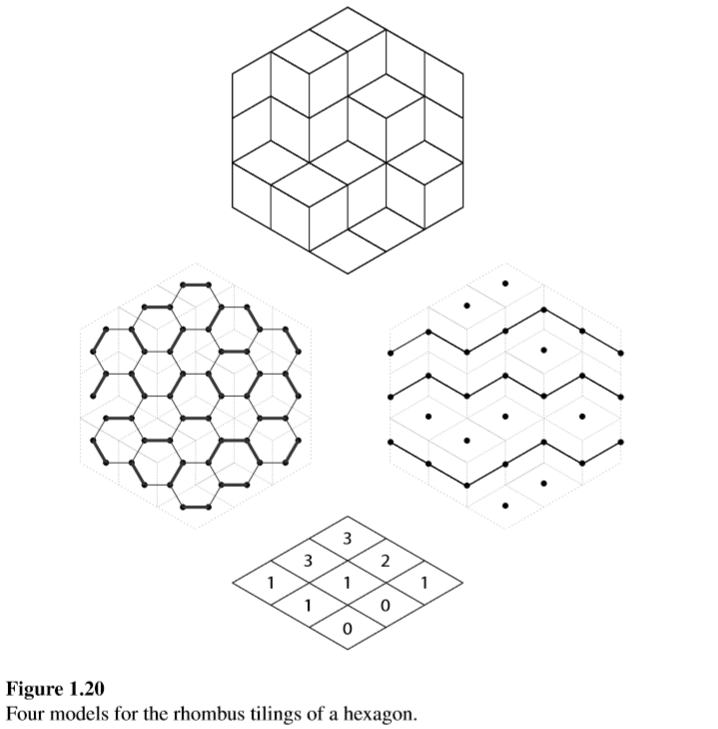
有几种观点：

看成正视图，如此，容易看到3种【$60^°120^°$的菱形】每种都是$n^2$个
思路是把每个菱形都看成是两个正三角形拼接，每个正三角形的中心作为一个节点，一般而言(内部的)每个节点和最近的3个节点相连。构成hexagonal grid。

相邻两个节点相连如果两个等边三角形上面正好是覆盖所用的菱形。问题转变为求完美匹配。
plane partition理解。从观点1的角度往前一步，给出【表明每个格子上垒有多少个cube】的俯视图。 an array of nonnegative integers(ﬁnitely many of which are non-zero)that is weakly decreasing in each row and column. We conclude that $R_n$ is also the number of plane partitions whose non-zero entries are at most n, and ﬁt inside an n×n square.
从观点1的角度出发，看高度$n-0.5$，...，高度2.5，高度1.5，高度0.5，截cube stack的曲线。这对应于 n sources S1,...,Sn on the left to the sinks T1,...,Tn ，（S1到T1,S2到T2....）的routing。利用前面的Lindstrm–Gessel–Viennot lemma，矩阵元素$\begin{gathered}
\begin{pmatrix} 2n \\ n+i-j \end{pmatrix}
\end{gathered}$

\[R_n=det\bigg[\begin{gathered}
\begin{pmatrix} 2n \\ n+i-j \end{pmatrix}\bigg]
\end{gathered}_{1\leq i,j\leq n}=\prod\limits_{i,j,k=1}^{n}\frac{i+j+k-1}{i+j+k-2}
\]

Example4 Catalan determinants, multitriangulations, and Pfafﬁan rings

定义一个序列$A=(a_0,a_1,a_2,...)$的Hankel矩阵$H_n(A)$和$H_n'(A)$

\[\begin{equation}
H_n(A)
=\begin{pmatrix}
a_0 & a_1 & \cdots\ &a_n\\
a_1 & a_2 & \cdots\ & a_{n+1}\\
\vdots & \vdots & \ddots & \vdots \\
a_n & a_{n+1} & \cdots\ & a_{2n}\\
\end{pmatrix}
\end{equation}
\]

和

\[\begin{equation}
H_n'(A)
=\begin{pmatrix}
a_1 & a_2 & \cdots\ &a_{n+1}\\
a_2 & a_3 & \cdots\ & a_{n+2}\\
\vdots & \vdots & \ddots & \vdots \\
a_{n+1}& a_{n+2} & \cdots\ & a_{2n+1}\\
\end{pmatrix}
\end{equation}
\]

如果我们知道 the Hankel determinants $det \ H_n(A)$ and $det\ H_n'(A)$ ，而且对所有的n它们都是非零的，我们可以利用递推关系从 $a_0,…, a_{k-1}$来恢复每一个 $a_k$ 。

如果序列是卡特兰序列$C=(C_0,C_1,C_2,...)$的话，恰好有一种很好的解释。

式(1.9)是许多事物的组合计数。

the number of k-fans of Dyck paths of length $2(n−2k)$

式（1.9）也是the number of k-fans of Dyck paths of length $2(n-2k)$

the number of k triangulations of an n-gon

k-crossing 定义 a k-crossing in an n-gon to be a set of k diagonals that cross pairwise（两两相交）

k-triangulation定义 A k-triangulation is a maximal set of diagonals with no(k+1)-crossings.

式(1.9)也是 the number of k triangulations of an n-gon 。

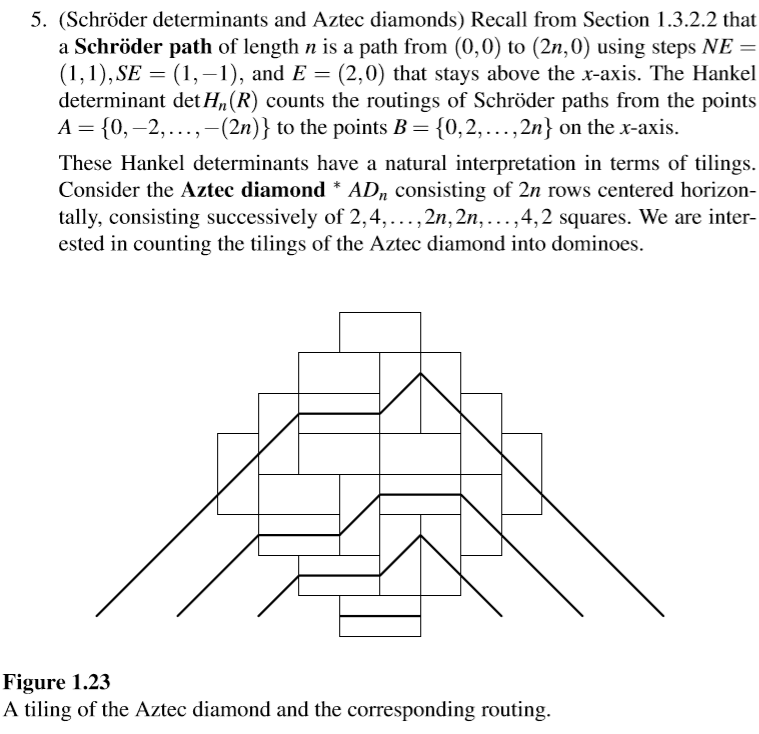
Example5 Schröder determinants and Aztec diamonds