P8881 懂事时理解原神

简要题意

\(T\) 组数据，每组数据给出一个 \(n\) 个顶点，\(m\) 条边的无向无权图。求出使用下面的伪代码求 \(1\) 为源点的单源最短路答案正确的概率。保留 \(3\) 位小数。

int dis[N],vis[N];// dis 是答案数组

void dfs(int u){
	vis[u]=1;
	vector<int> vct;
	for(int i=1;i<=n;i++){
		if(!vis[i] && 存在边(u,i)){
			vct.push_back(i);
		}
	}
	random_shuffle(vct.begin(),vct.end());
	for(int i:vct){
		dis[v]=dis[u]+1;
		dfs(i);
	}
}

void solve(){
	for(int i=1;i<=n;i++){
		vis[i]=0;
		dis[i]=-1;
	}
	dis[1]=0;
	dfs(1);
}

对于 \(100\%\) 的数据，\(1\le n,m\le 50000，1\le T\le 10\)，保证所输入的图无重边、自环。

思路

可以看出，这个最短路非常像求树的深度。树有一个重要的性质就是不存在环。如果有环一定错了。

为什么？因为如果存在一个环，像这样：

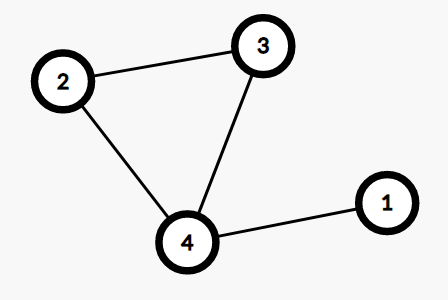
模拟一遍：

• \(\operatorname{dis}_1=0\)
• \(\operatorname{dis}_4=1\)
• 如果先遍历 \(2\)，那么 \(\operatorname{dis}_2=2\)，否则 \(\operatorname{dis}_3=2\)。
• 如果上一步先遍历 \(2\)，那么 \(\operatorname{dis}_3=3\)，否则 \(\operatorname{dis}_2=3\)。

正确的 \(\operatorname{dis}_2=2,\operatorname{dis}_3=2\)，而该算法都算错了。

读者可以再枚举几个，可以发现，环上节点会算错。这时候，如果环上再接出去一个节点，那么它依然会算错。

于是得出结论：如果存在从 \(1\) 出发的环。那么答案是 \(0.000\)，否则答案是 \(1.000\)。

并查集解决。时间复杂度 \(O(T(m+n)\log n)\)。

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 50005;
int fa[N],t,n,m;
bool tag[N];

int find(int x){
	if(fa[x]==x)return x;
	else return fa[x]=find(fa[x]);
}

inline void merge(int u,int v){
	if(find(u)==find(v)){
		tag[find(v)]=1;
		return;
	}
	fa[find(u)]=find(v);
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	cin>>t;
	while(t--){
		cin>>n>>m;
		for(int i=1;i<=n;i++) fa[i]=i;
		for(int i=1;i<=n;i++) tag[i]=0;
		for(int i=1,u,v;i<=m;i++){
			cin>>u>>v;
			merge(u,v);
		}
		bool flag=1;
		for(int i=1;i<=n;i++){
			if(find(1)==find(i)&&tag[i]){
				cout<<"0.000\n";
				flag=0;
				break;
			}
		}
		if(flag) cout<<"1.000\n";
	}
	return 0;
}