基于python的数学建模---最小二乘拟合

- import numpy as np
- import matplotlib.pyplot as plt
- from scipy.optimize import leastsq
- from matplotlib.pylab import mpl
- mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 指定默认字体
- mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
- # 计算以p为参数的直线与原始数据之间误差
- def f(p):
- k, b = p
- return Y - (k * X + b)
- if __name__ == '__main__':
- X = np.array([8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78])
- Y = np.array([7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05])
- # leastsq使得f的输出数组的平方和最小,参数初始值为[1,0]
- r = leastsq(f, [1, 0]) # 数初始值可以随便设个合理的
- k, b = r[0]
- x = np.linspace(0, 10, 1000)
- y = k * x + b
- # 画散点图,s是点的大小
- plt.scatter(X, Y, s=100, alpha=1.0, marker='o', label=u'数据点')
- # 话拟合曲线,linewidth是线宽
- plt.plot(x, y, color='r', linewidth=2, linestyle="-", markersize=20, label=u'拟合曲线')
- plt.xlabel('安培/A')
- plt.ylabel('伏特/V')
- plt.legend(loc=0, numpoints=1) # 显示点和线的说明
- # plt.plot(X, Y)
- plt.show()
- print('k = ', k)
- print('b = ', b)
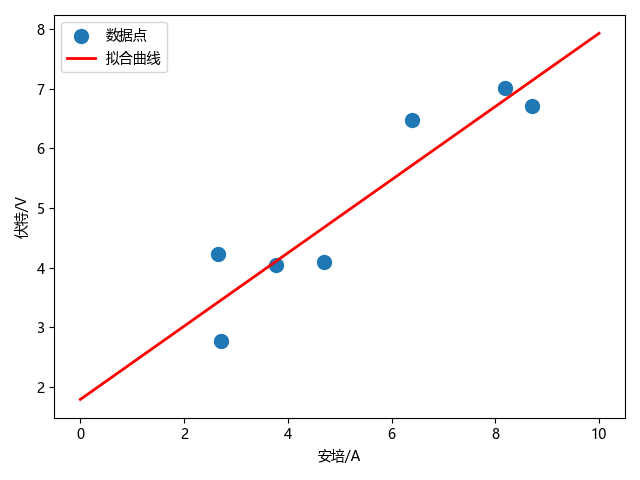
k = 0.6134953491930442
b = 1.794092543259387
- 下面是用anaconda写的
- import numpy as np
- import matplotlib.pyplot as plt
- np.set_printoptions(suppress=True) # 取消科学计数法
- x = np.array([8.19,2.72,6.39,8.71,4.7,2.66,3.78])
- y = np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])
- plt.figure()
- plt.scatter(x,y)
plt.show()

- from scipy.optimize import leastsq
- def error(p,x,y):
- return p[0]*x + p[1] - y
- p0 = [2,2] #设置初始值
- res = leastsq(error,p0,args=(x,y))
- k,b = res[0]
- print(k)
- print(b)
- 0.6134953485739788
- 1.7940925393506084
- x1 = np.linspace(0,9,1000)
- y1 = k*x1+b
- plt.scatter(x,y,color= 'orange',label = 'Sample Point')
- plt.plot(x1,y1,color= 'red',label = 'Fitting Line')
- plt.legend()
- plt.show()
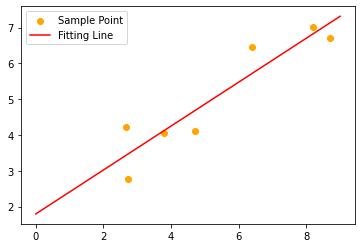
基于python的数学建模---最小二乘拟合的更多相关文章
- 使用Python scipy linprog 线性规划求最大值或最小值(使用Python学习数学建模笔记)
函数格式 scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='simp ...
- Python数学建模-01.新手必读
Python 完全可以满足数学建模的需要. Python 是数学建模的最佳选择之一,而且在其它工作中也无所不能. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数学 ...
- Python小白的数学建模课-A1.国赛赛题类型分析
分析赛题类型,才能有的放矢. 评论区留下邮箱地址,送你国奖论文分析 『Python小白的数学建模课 @ Youcans』 带你从数模小白成为国赛达人. 1. 数模竞赛国赛 A题类型分析 年份 题目 要 ...
- Python小白的数学建模课-B5. 新冠疫情 SEIR模型
传染病的数学模型是数学建模中的典型问题,常见的传染病模型有 SI.SIR.SIRS.SEIR 模型. 考虑存在易感者.暴露者.患病者和康复者四类人群,适用于具有潜伏期.治愈后获得终身免疫的传染病. 本 ...
- Python小白的数学建模课-B6. 新冠疫情 SEIR 改进模型
传染病的数学模型是数学建模中的典型问题,常见的传染病模型有 SI.SIR.SIRS.SEIR 模型. SEIR 模型考虑存在易感者.暴露者.患病者和康复者四类人群,适用于具有潜伏期.治愈后获得终身免疫 ...
- Python小白的数学建模课-12.非线性规划
非线性规划是指目标函数或约束条件中包含非线性函数的规划问题,实际就是非线性最优化问题. 从线性规划到非线性规划,不仅是数学方法的差异,更是解决问题的思想方法的转变. 非线性规划问题没有统一的通用方法, ...
- Python数学建模-02.数据导入
数据导入是所有数模编程的第一步,比你想象的更重要. 先要学会一种未必最佳,但是通用.安全.简单.好学的方法. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数据导入 ...
- Python小白的数学建模课-A3.12 个新冠疫情数模竞赛赛题与点评
新冠疫情深刻和全面地影响着社会和生活,已经成为数学建模竞赛的背景帝. 本文收集了与新冠疫情相关的的数学建模竞赛赛题,供大家参考,欢迎收藏关注. 『Python小白的数学建模课 @ Youcans』带你 ...
- Python小白的数学建模课-07 选址问题
选址问题是要选择设施位置使目标达到最优,是数模竞赛中的常见题型. 小白不一定要掌握所有的选址问题,但要能判断是哪一类问题,用哪个模型. 进一步学习 PuLP工具包中处理复杂问题的字典格式快捷建模方法. ...
- Python小白的数学建模课-09 微分方程模型
小白往往听到微分方程就觉得害怕,其实数学建模中的微分方程模型不仅没那么复杂,而且很容易写出高水平的数模论文. 本文介绍微分方程模型的建模与求解,通过常微分方程.常微分方程组.高阶常微分方程 3个案例手 ...
随机推荐
- KingbaseES 实现MYSQL hex/unhex 函数
MySQL 的hex 和 unhex 函数类似于KingbaseES 的encode 和 decoding,实现字符与16进制之间的转换. 一.先看MySQL例子 mysql> select h ...
- 果汁 DI 介绍
Guice (英音同 'juice[果汁]') 是一个为 JDK8 及以上提供的轻量依赖注入框架. 目录 三级标题 三级标题 四级标题 三级标题 三级标题 /** * Animal */ interf ...
- JS中如何删除某个父元素下的所有子元素?
JS中如何删除某个父元素下的所有子元素?这里我介绍几种方法: 1.通过元素的 innerHTML 属性来删除 这种方式我觉得是最有方便的,直接找到你想要的父元素,直接令其 element.innerH ...
- 输入法词库解析(六)QQ 拼音分类词库.qpyd
详细代码:https://github.com/cxcn/dtool 前言 .qpyd 是 QQ 拼音输入法 6.0 以下版本所用的词库格式,可以在 http://cdict.qq.pinyin.cn ...
- Elasticsearch: Ngrams, edge ngrams, and shingles
Ngrams和edge ngrams是在Elasticsearch中标记文本的两种更独特的方式. Ngrams是一种将一个标记分成一个单词的每个部分的多个子字符的方法. ngram和edge ngra ...
- Elasticsearch Dockerfile 例子
文章转载自:https://elasticstack.blog.csdn.net/article/details/111692444 前提条件 在继续执行本教程中概述的步骤之前,你需要具备一个关键的先 ...
- 1-VSCode搭建GD32开发环境
一.使用VSCode开发GD32的原因 1-单片机开发用的最多的IDE为Keil,而Keil为商用软件,并非开源,而且只支持windows环境,介于当前关系,有断供的风险在. 2-其他IDE类似第1条 ...
- day43-反射02
2.Class类 2.1基本介绍 Class类也是类,因此也继承Object类 Class类对象不是new出来的,而是系统创建的 对于某个类的Class类对象,在内存中只有一份,因为类只加载一次 每个 ...
- Docker容器虚拟化
Docker容器虚拟化 目录 Docker容器虚拟化 虚拟化网络 单节点容器间通信 不同节点容器间通信 虚拟化网络 Network Namespace 是 Linux 内核提供的功能,是实现网络虚拟化 ...
- Java学生管理系统(详解)
相信大部分人都有接触过这个 Java 小项目--学生管理系统,下面会分享我在做这个项目时的一些方法以及程序代码供大家参考(最后附上完整的项目代码). 首本人只是个初学Java的小白,可能项目中有许多地 ...
