HDU 1025 Constructing Roads In JGShining's Kingdom （DP）

Problem Description

JGShining's kingdom consists of 2n(n is no more than 500,000) small cities which are located in two parallel lines.



Half of these cities are rich in resource (we call them rich cities) while the others are short of resource (we call them poor cities). Each poor city is short of exactly one kind of resource and also each rich city is rich in exactly one kind of resource.
You may assume no two poor cities are short of one same kind of resource and no two rich cities are rich in one same kind of resource. 



With the development of industry, poor cities wanna import resource from rich ones. The roads existed are so small that they're unable to ensure the heavy trucks, so new roads should be built. The poor cities strongly BS each other, so are the rich ones. Poor
cities don't wanna build a road with other poor ones, and rich ones also can't abide sharing an end of road with other rich ones. Because of economic benefit, any rich city will be willing to export resource to any poor one.



Rich citis marked from 1 to n are located in Line I and poor ones marked from 1 to n are located in Line II. 



The location of Rich City 1 is on the left of all other cities, Rich City 2 is on the left of all other cities excluding Rich City 1, Rich City 3 is on the right of Rich City 1 and Rich City 2 but on the left of all other cities ... And so as the poor ones. 



But as you know, two crossed roads may cause a lot of traffic accident so JGShining has established a law to forbid constructing crossed roads.



For example, the roads in Figure I are forbidden.








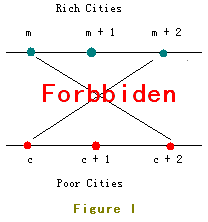
In order to build as many roads as possible, the young and handsome king of the kingdom - JGShining needs your help, please help him. ^_^

 

Input

Each test case will begin with a line containing an integer n(1 ≤ n ≤ 500,000). Then n lines follow. Each line contains two integers p and r which represents that Poor City p needs to import resources from Rich City r. Process to the end of file.

 

Output

For each test case, output the result in the form of sample. 

You should tell JGShining what's the maximal number of road(s) can be built. 

 

Sample Input

2
1 2
2 1
3
1 2
2 3
3 1

 

Sample Output

Case 1:
My king, at most 1 road can be built.

Case 2:
My king, at most 2 roads can be built.

Hint

Huge input, scanf is recommended.


假设你想是二分匹配就错了，事实上是个LIS。。。
题意：穷国连接富国，不能交叉，问最大的对数
注意输出的road(len=1)和roads(len>1)。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<limits.h>
using namespace std;
const int maxn=500000+50;
int a[maxn],num[maxn];
int main()
{
    int n,x,y;
    int cas=0;
    while(~scanf("%d",&n))
    {
        for(int i=0;i<n;i++)
        {
            scanf("%d%d",&x,&y);
            a[x]=y;//穷国x的值为y，求最大LIS（最大上升子列）
        }
        num[1]=a[1];
        int len=1;
        int l,r,mid,ans;
        for(int i=2;i<=n;i++)//LIS的优化写法
        {
            l=1;
            r=len;
            while(l<=r)
            {
                mid=(l+r)>>1;
                if(num[mid]>=a[i])
                    r=mid-1;
                else
                    l=mid+1;
            }
            num[l]=a[i];
            if(l>len)
                len++;
        }
        printf("Case %d:\n",++cas);
        if(len==1) printf("My king, at most %d road can be built.\n\n",len);
        else   printf("My king, at most %d roads can be built.\n\n",len);
    }
    return 0;
}