《A First Course in Probability》-chape4-离散型随机变量-几种典型分布列

超几何分布：

超几何分布基于这样一个模型，一个坛子中有N个球，其中m个白球，N-m个黑球，从中随机取n(不放回)，令X表示取出来的白球数，那么：

我们称随机变量X满足参数为(n,m,M)的超几何分布。

考察其期望的求法：

几何分布：

在独立重复实验当中，每一次实验成功的概率是p，我们关注使得实验成功一次所需要重复的实验次数n及其对应的概率，很容易看到，我们有如下的分布列：

验证其作为分布列的性质：

几何分布的期望：

根据期望的定义，并在这里设q = 1-p

二项分布：

基于最基础的一个离散型随机变量——伯努利随机变量X，我们进行n次重复的实验，其概率分布结果就是所谓的二项分布。

具体点来说，就是某个实验成功的概率是p，现在我们进行n此时杨，设随机变量X表示n次实验后成功的次数，那么有如下分布列成立。

关于其期望，推导过程和几何分布、超几何分布中期望的推导是同质的，先推出X^k的表达式，然后根据二项式恒等关系，寻求自相似性建立递推关系，然后得到最终的期望值、方差。

关于二项分布概率值的单调性这里有这样一个命题：对于满足参数为（n,p）的二项随机变量，k取得[0,n]时，P{X=k}先递增，后递减，当k = (n+1)p时取得最大值。

基于我们最为熟悉的离散型分布——二项分布，我们能够衍生出很多别的分布列，对于之前介绍过的几何分布，我们赋予其的含义是：某个事件成功的概率是p，在n次独立重复实验中恰好成功一次的概率是多少。顺着这层含义，我们把1次编程r次，便得到了所谓的负二项分布。设负二项分布的随机变量是X，独立事件成功的概率是p，则在n次重复独立实验中恰好成功r次的概率是：

较之二项分布，我们能够看到，负二项分布更加强调n次重复实验中“恰好”成功r次，也就是要求第n次实验恰好是第r次成功的实验。

我们通过一个问题来进行举例——巴拿赫火柴问题。

Q：某个抽烟的数学家总是随身带着两盒火柴，一盒放在左边口袋一盒放在右边口袋。每次他需要火柴时，他就从任意的口袋中的火柴盒中取出一个火柴，现在两盒火柴中都各有N个火柴，那么请问他第一次发现其中一个盒子已经空了的时候，另一盒恰好有k根火柴的概率有多大？

分析：首先我们需要讨论的一个点是，这个火柴位于哪个口袋的火柴盒是空的，显然是左是右具有对称性，我们分析一种情况，进行平方即可。

假设左口袋为空，那么这个过程的最后一个步骤显然是在数学家第2N-k次取火柴的时候，必然取走了右口袋中的一根火柴，这是一位他拿走左口袋的最后一根火柴的时候，我们就可以默认理性的数学家不会再去拿左口袋的火柴盒，因此我们就可以将其与负二项分布联系起来：在2N-k次重复实验当中，恰好有N次从左口袋取出的概率。

即

当然，这道问题的最终结果是将这个概率平方。

负二项分布的期望：

直接推导是难以给出E[X]有关负二项分布的参数r、p的联系的，因此这里我们考虑建立递推关系。

结合之前复合随机变量的计算法则，我们在这里容易得到如下的等式。

从二项分布结合级数推导而来的泊松分布：

对于二项分布我们很熟悉，在生活当中我们也很常用，但是其计算公式不免显得有点繁琐，我们现进行如下的简化推导：

设某个二项分布的参数是(n,p)，设置参数λ=np.随机变量为X.

同时结合几种极限求法，我们能够看到，当n趋近于无穷的时候，有：

因此我们得到：

这便是泊松分布列。容易看到，n趋近于无穷的二项分布可以与泊松分布等价，如果基于n趋近于无穷，我们可以验证泊松分布的作为分布列的一个性质：

泊松分布的数字特征：

下面讨论泊松分布的期望和方差。

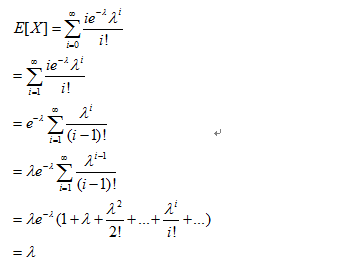
Ps：推导过程用到了泰勒级数的展开式，具体的内容笔者在《托马斯大学微积分》的专栏中会给出。