HDU-4570 Multi-bit Trie

http://acm.hdu.edu.cn/showproblem.php?pid=4570

Multi-bit Trie

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 446    Accepted Submission(s): 169

Problem Description

　　IP lookup is one of the key functions of routers for packets forwarding and classifying. Generally, IP lookup can be simplified as a Longest Prefix Matching (LPM) problem. That's to find the longest prefix in the Forwarding Information Base (FIB) that matches the input packet's destination address, and then output the corresponding Next Hop information.

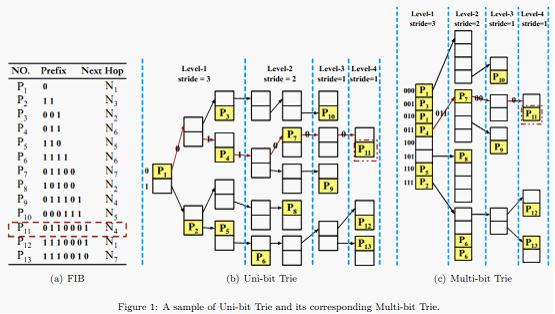
　　Trie-based solution is the most wildly used one to solve LPM. As shown in Fig.1(b), an uni-bit trie is just a binary tree. Processing LPM on it needs only traversing it from the root to some leaf, according to the input packet's destination address. The longest prefix along this traversing path is the matched one. In order to reduce the memory accesses for one lookup, we can compress some consecutively levels of the Uni-bit Trie into one level, transforming the Uni-bit Trie into a Multi-bit Trie.
　　For example, suppose the strides array is {3, 2, 1, 1}, then we can transform the Uni-bit Trie shown in Fig.1(b) into a Multi-bit Trie as shown in Fig.1(c). During the transforming process, some prefixes must be expanded. Such as 11(P2), since the first stride is 3, it should be expanded to 110(P2) and 111(P2). But 110(P5) is already exist in the FIB, so we only store the longer one 110(P5).
　　Multi-bit Trie can obviously reduce the tree level, but the problem is how to build a Multi-bit Trie with the minimal memory consumption (the number of memory units). As shown in Fig.1, the Uni-bit Trie has 23 nodes and consumes 46 memory units in total, while the Multi-bit Trie has 12 nodes and consumes 38 memory units in total.

 

Input

　　The first line is an integer T, which is the number of testing cases.
　　The first line of each case contains one integer L, which means the number of levels in the Uni-bit Trie.
　　Following L lines indicate the nodes in each level of the Uni-bit Trie.
　　Since only 64 bits of an IPv6 address is used for forwarding, a Uni-bit Trie has maximal 64 levels. Moreover, we suppose that the stride for each level of a Multi-bit Trie must be less than or equal to 20.

 

Output

　　Output the minimal possible memory units consumed by the corresponding Multi-bit Trie.

 

Sample Input

1

7

1 2 4 4 5 4 3

 

Sample Output

38

题意真难懂。

题意：这题题意确实有点难懂，起码对于我这个英语渣渣来说是这样，于是去别人的博客看了下题目意思，归纳起来如下：

给出一个长度为n的数列，将其分成若干段，要求最小，其中ai是每一段数列的第一项，bi是每一段的长度，l为将数列分成l段。

比如样例：n=7，A={1 2 4 4 5 4 3}，将其分成1 2 4| 4 5| 4| 3，则其所用空间为1*2^3+4*2^2+4*2^1+3*2^1=38，而如果分成1 2| 4 4 5| 4 3，则其所用空间为1*2^2+4*2^3+4*2^2=52，比38大。

思路：区间DP，

dp[i][j]表示i--j层最小的内存；

初始条件：全压缩或全不压缩

因为压缩不能超过20层，所以在小于20层时初始条件：

dp[i][j]=a[i]*fun(2,(j-i+1));

大于20层是只能不压缩

dp[i][j]=(sum[j]-sum[i-1])*2;

然后循环

dp[i][j]=min(dp[i][k]+dp[k+1][j],dp[i][j]); k:i...j;

 

Source

2013 ACM-ICPC长沙赛区全国邀请赛——题目重现

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
__int64 dp[][];
 __int64 a[],sum[];
__int64 fun(int x,__int64 y)
{
    int i;
     __int64 ans=;
    for(i=;i<=y;i++)
        ans=ans*x;
    return ans;
}
int main()
{
    int i,t,n,j,k,g;
    scanf("%d",&t);
    while(t--)
    {
        memset(dp,,sizeof(dp));
         memset(sum,,sizeof(sum));
         memset(a,,sizeof(a));
         scanf("%d",&n);
       for(i=;i<n;i++)
         {
             scanf("%I64d",&a[i]);
        }
         sum[]=a[];
         for(i=;i<n;i++)
             sum[i]=sum[i-]+a[i];

        for(k=;k<n;k++)
        {
           for(i=;i<n-k;i++)
            {
                   j=i+k;
                   if(k<)//区间小于20层,全压缩
                     dp[i][j]=a[i]*fun(,(j-i+));
                   else
                      dp[i][j]=(sum[j]-sum[i-])*;//区间多于20，全不压缩
               for(g=i;g<=j;g++)
               {

                   dp[i][j]=min(dp[i][j],dp[i][g]+dp[g+][j]);

               }
            }
        }

       printf("%I64d\n",dp[][n-]);
    }
    return ;
}
/*
1
7
1
2
4
4
5
4
3
*/