LinGo:装货问题——线性规划,整数规划,1988年美国数模B题

7种规格的包装箱要装有两辆铁路平板车上去，包装箱的宽和高相同，但厚度（t,以cm计）和重量（以kg计）不同，

表A-1给出了每包装箱的厚度、重量和数量，每辆车有10.2m长的地方用来装包装箱（像面包片那样），车的载重为40吨，

对C₅、C₆、C₇、规格的包装箱的总数有一个特殊的限制：这些规格箱子所占的空间（厚度）不能超过302.7cm。

试把包装箱装到两辆平板车上去（图A-6）使得浪费的空间最小。

表A-1 每种包装箱的厚度、重量和数量

C₁

C₂

C₃

C₄

C₅

C₆

C₇

t(cm)

w(kg)

48.7

2000

52.0

3000

61.3

1000

72.0

500

48.7

4000

52.0

2000

64.0

1000

解：

一.设决策变量：

　　 X_ij表示第i辆平板车放j类包装箱X_ij件

t_j为第j个包装箱的厚度(cm)

w_j为第j个包装箱的重量(kg)

n_j表示第j个包装箱的数量

二.分析约束条件

1. 两辆车上的各种包装箱数量必须小于等于各类包装箱的总数

2.每辆车上的载重必须小于等于400000kg

3.每辆车上包装箱的长度必须小于等于1020cm

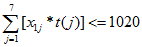
4. C₅、C₆、C₇、规格的包装箱的总厚度不能超过302.7cm

5.包装箱的件数必须是整数

@for(link(i,j) : @gin(x(i,j)));

三.目标函数

[OBJ] min = 2040 - @sum(link(i,j) : x(i,j)*t(j));

四.LinGo代码

model:

sets:

    row/../;

    col/../ : t, w, n;

    link(row, col) : x;

endsets

data:

    t = 48.7, 52.0, 61.3, 72.0, 48.7, 52.0, 64.0;

    w = , , , , , , ;

    n = , , , , , , ;

enddata

@for(col(j) : @sum(row(i) : x(i,j)) <= n(j));

@for(row(i) : @sum(col(j) : x(i,j)*w(j)) <= );

@for(row(i) : @sum(col(j) : x(i,j)*t(j)) <= );

@sum(row(i) : @sum(col(j) | j#ge# : x(i,j) * t(j) )) <= 302.7;

@for(link(i,j) : @gin(x(i,j)));

[OBJ] min = 2040 - @sum(link(i,j) : x(i,j)*t(j));

end

五.LinGo运算结果

Global optimal solution found.
Objective value:                             0.6000000
Objective bound:                             0.6000000
Infeasibilities:                              0.000000
Extended solver steps:                            9342
Total solver iterations:                         40250

Variable           Value        Reduced Cost
                          T( 1)        48.70000            0.000000
                          T( 2)        52.00000            0.000000
                          T( 3)        61.30000            0.000000
                          T( 4)        72.00000            0.000000
                          T( 5)        48.70000            0.000000
                          T( 6)        52.00000            0.000000
                          T( 7)        64.00000            0.000000
                          W( 1)        2000.000            0.000000
                          W( 2)        3000.000            0.000000
                          W( 3)        1000.000            0.000000
                          W( 4)        500.0000            0.000000
                          W( 5)        4000.000            0.000000
                          W( 6)        2000.000            0.000000
                          W( 7)        1000.000            0.000000
                          N( 1)        8.000000            0.000000
                          N( 2)        7.000000            0.000000
                          N( 3)        9.000000            0.000000
                          N( 4)        6.000000            0.000000
                          N( 5)        6.000000            0.000000
                          N( 6)        4.000000            0.000000
                          N( 7)        8.000000            0.000000
                       X( 1, 1)        8.000000           -48.70000
                       X( 1, 2)        1.000000           -52.00000
                       X( 1, 3)        0.000000           -61.30000
                       X( 1, 4)        6.000000           -72.00000
                       X( 1, 5)        3.000000           -48.70000
                       X( 1, 6)        0.000000           -52.00000
                       X( 1, 7)        0.000000           -64.00000
                       X( 2, 1)        0.000000           -48.70000
                       X( 2, 2)        6.000000           -52.00000
                       X( 2, 3)        9.000000           -61.30000
                       X( 2, 4)        0.000000           -72.00000
                       X( 2, 5)        0.000000           -48.70000
                       X( 2, 6)        3.000000           -52.00000
                       X( 2, 7)        0.000000           -64.00000

Row    Slack or Surplus      Dual Price
                              1        0.000000            0.000000
                              2        0.000000            0.000000
                              3        0.000000            0.000000
                              4        0.000000            0.000000
                              5        3.000000            0.000000
                              6        1.000000            0.000000
                              7        8.000000            0.000000
                              8        366000.0            0.000000
                              9        367000.0            0.000000
                             10       0.3000000            0.000000
                             11       0.3000000            0.000000
                             12       0.6000000            0.000000
                            OBJ       0.6000000           -1.000000

结论：

浪费空间最小为：0.6cm

　　　　C1　　C2　　C3　　C4　　C5　　C6　　C7

第一辆　8　　 1　　 0 　　 6　　 3　　 0 　　 0

第二辆 0　　 6 　　 9　　 0　　 0　　 3　　 0

LinGo:装货问题——线性规划,整数规划,1988年美国数模B题的更多相关文章

Python数模笔记-Scipy库（1）线性规划问题
1.最优化问题建模最优化问题的三要素是决策变量.目标函数和约束条件. (1)分析影响结果的因素是什么,确定决策变量 (2)决策变量与优化目标的关系是什么,确定目标函数 (3)决策变量所受的限制条件是 ...
LinGo:疏散问题——线性规划,0-1规划
个部门(A.B.C.D.E)组成.现要将它的几个部门迁出甲市,迁至乙市或丙市. (每个城市最多接纳三个部门) 除去因政府鼓励这样做以外,还有用房便宜,招工方便等好处.对这些好处已作出数量估计,其值如下 ...
LinGo:投资问题——线性规划
一.根据题目所给数据,建立一张表格方便查看项目A 项目B 项目C 项目D 可投资年 1,2,3,4 3 2 1,2,3,4,5 收回本利年次年年末第5年第5年当年年末本利 1.06 1.1 ...
Python数模笔记-PuLP库（1）线性规划入门
1.什么是线性规划线性规划(Linear programming),在线性等式或不等式约束条件下求解线性目标函数的极值问题,常用于解决资源分配.生产调度和混合问题.例如: max fx = 2*x1 ...
数模常用算法系列Matlab实现-----线性规划
线性规划的 Matlab 标准形式线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以是小于号也可以是大于号.为了避免这种形式多样性带来的不便,Matlab 中规定线性规划的标 ...
Python数模笔记-PuLP库（2）线性规划进阶
1.基于字典的创建规划问题上篇中介绍了使用 LpVariable 对逐一定义每个决策变量,设定名称.类型和上下界,类似地对约束条件也需要逐一设置模型参数.在大规模的规划问题中,这样逐个定义变量和设置 ...
模拟退火算法Python编程（3）整数规划问题
1.整数规划问题整数规划问题在工业.经济.国防.医疗等各行各业应用十分广泛,是指规划中的变量(全部或部分)限制为整数,属于离散优化问题(Discrete Optimization). 线性规划问题的 ...
Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
Python小白的数学建模课-04.整数规划
整数规划与线性规划的差别只是变量的整数约束. 问题区别一点点,难度相差千万里. 选择简单通用的编程方案,让求解器去处理吧. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达 ...

随机推荐

Android Camera开发:使用GLSurfaceView预览Camera 基础拍照
GLSurfaceView是OpenGL中的一个类,也是可以预览Camera的,而且在预览Camera上有其独到之处.独到之处在哪?当使用Surfaceview无能为力.痛不欲生时就只有使用GLSur ...
Python 函数的使用外加引入文件
#coding=utf-8 #!user/bin/python import sys import test2 def functionsss(name,sex,age=25): print name ...
MD5加密相关
demo效果
ASP.NET MVC with Entity Framework and CSS一书翻译系列文章之第三章：搜索、高级过滤和视图模型
在这一章中,我们首先添加一个搜索产品的模块以增强站点的功能,然后使用视图模型而不是ViewBag向视图传递复杂数据. 注意:如果你想按照本章的代码编写示例,你必须完成第二章或者直接从www.apres ...
Centos7下Intel与AMD双显卡驱动的安装
前2天,在Nvidia单显卡上成功安装上了NVIdia的驱动,一时兴起,拿出另外的一个HP笔记本也准备装上驱动,悲催的是HP的显卡是AMD的,更加.更加悲催的是还是Intel+AMD的双显卡.网络 ...
浅析a标签的4个伪类 .
关于伪类,大家最熟悉的还是a标签的4个伪类::link 有链接属性时:visited 链接地址已被访问过:active 被用户激活(在鼠标点击与释放之间发生的事件):hov ...
JS冒泡事件与处理
JavaSciprt事件中有两个很重要的特性:事件冒泡以及目标元素. 事件冒泡: 当一个元素上的事件被触发的时候,比如说鼠标点击了一个按钮,同样的事件将会在那个元素的所有祖先元素中被触发.这一过程被 ...
wamp虚拟机配置
1.找到httpd.conf 里面:找到 # Virtual hosts 开启虚拟机Include conf/extra/httpd-vhosts.conf 2 编辑httpd-vhosts.con ...
HTTP协议学习-01
在学习一门新知识前还是先了解一下这个知识的一点点背景吧! http是属于协议层当中的最顶层的应用层,的面向对象的协议:它于 1990 年提出, 经过几年的使用与发展, 得到不断地完善和扩展. 目前在 ...
python3和Python2的区别（被坑太久了）
print函数:(Python3中print为一个函数,必须用括号括起来:Python2中print为class) Python 2 的 print 声明已经被 print() 函数取代了,这意味着我 ...

LinGo:装货问题——线性规划,整数规划,1988年美国数模B题

LinGo:装货问题——线性规划,整数规划,1988年美国数模B题的更多相关文章

随机推荐

热门专题