Typeclassopedia

https://wiki.haskell.org/wikiupload/8/85/TMR-Issue13.pdf

By Brent Yorgey, byorgey@gmail.com

Originally published 12 March 2009 in issue 13 of the Monad.Reader. Ported to the Haskell wiki in November 2011 by Geheimdienst.

This is now the official version of the Typeclassopedia and supersedes the version published in the Monad.Reader. Please help update and extend it by editing it yourself or by leaving comments, suggestions, and questions on the talk page.

Contents

[hide] 

• 1 Abstract
• 2 Introduction
• 3 Functor
  • 3.1 Definition
  • 3.2 Instances
  • 3.3 Laws
  • 3.4 Intuition
  • 3.5 Utility functions
  • 3.6 Further reading
• 4 Applicative
  • 4.1 Definition
  • 4.2 Laws
  • 4.3 Instances
  • 4.4 Intuition
  • 4.5 Utility functions
  • 4.6 Alternative formulation
  • 4.7 Further reading
• 5 Monad
  • 5.1 Definition
  • 5.2 Instances
  • 5.3 Intuition
  • 5.4 Utility functions
  • 5.5 Laws
  • 5.6 do notation
  • 5.7 Further reading
• 6 MonadFail
  • 6.1 Definition
  • 6.2 Law
• 7 Monad transformers
  • 7.1 Standard monad transformers
  • 7.2 Definition and laws
  • 7.3 Transformer type classes and "capability" style
  • 7.4 Composing monads
  • 7.5 Further reading
• 8 MonadFix
  • 8.1 do rec notation
  • 8.2 Examples and intuition
  • 8.3 mdo syntax
  • 8.4 Further reading
• 9 Semigroup
  • 9.1 Definition
  • 9.2 Laws
• 10 Monoid
  • 10.1 Definition
  • 10.2 Laws
  • 10.3 Instances
  • 10.4 Further reading
• 11 Failure and choice: Alternative, MonadPlus, ArrowPlus
  • 11.1 Definition
  • 11.2 Instances
  • 11.3 Laws
  • 11.4 Utility functions
  • 11.5 Further reading
• 12 Foldable
  • 12.1 Definition
  • 12.2 Instances and examples
  • 12.3 Derived folds
  • 12.4 Utility functions
  • 12.5 Foldable actually isn't
  • 12.6 Further reading
• 13 Traversable
  • 13.1 Definition
  • 13.2 Intuition
  • 13.3 Instances and examples
  • 13.4 Laws
  • 13.5 Further reading
• 14 Bifunctor
  • 14.1 Definition
  • 14.2 Laws
  • 14.3 Instances
• 15 Category
  • 15.1 Further reading
• 16 Arrow
  • 16.1 Definition
  • 16.2 Intuition
  • 16.3 Instances
  • 16.4 Laws
  • 16.5 ArrowChoice
  • 16.6 ArrowApply
  • 16.7 ArrowLoop
  • 16.8 Arrow notation
  • 16.9 Further reading
• 17 Comonad
  • 17.1 Definition
  • 17.2 Further reading
• 18 Acknowledgements
• 19 About the author
• 20 Colophon

1 Abstract

The standard Haskell libraries feature a number of type classes with algebraic or category-theoretic underpinnings. Becoming a fluent Haskell hacker requires intimate familiarity with them all, yet acquiring this familiarity often involves combing through a mountain of tutorials, blog posts, mailing list archives, and IRC logs.

The goal of this document is to serve as a starting point for the student of Haskell wishing to gain a firm grasp of its standard type classes. The essentials of each type class are introduced, with examples, commentary, and extensive references for further reading.

2 Introduction

Have you ever had any of the following thoughts?

• What the heck is a monoid, and how is it different from a monad?

• I finally figured out how to use Parsec with do-notation, and someone told me I should use something called Applicative instead. Um, what?

• Someone in the #haskell IRC channel used (***), and when I asked Lambdabot to tell me its type, it printed out scary gobbledygook that didn’t even fit on one line! Then someone used fmap fmap fmapand my brain exploded.

• When I asked how to do something I thought was really complicated, people started typing things like zip.ap fmap.(id &&& wtf) and the scary thing is that they worked! Anyway, I think those people must actually be robots because there’s no way anyone could come up with that in two seconds off the top of their head.

If you have, look no further! You, too, can write and understand concise, elegant, idiomatic Haskell code with the best of them.

There are two keys to an expert Haskell hacker’s wisdom:

1. Understand the types.
2. Gain a deep intuition for each type class and its relationship to other type classes, backed up by familiarity with many examples.

It’s impossible to overstate the importance of the first; the patient student of type signatures will uncover many profound secrets. Conversely, anyone ignorant of the types in their code is doomed to eternal uncertainty. “Hmm, it doesn’t compile ... maybe I’ll stick in an fmap here ... nope, let’s see ... maybe I need another (.) somewhere? ... um ...”

The second key—gaining deep intuition, backed by examples—is also important, but much more difficult to attain. A primary goal of this document is to set you on the road to gaining such intuition. However—

There is no royal road to Haskell. —Euclid

This document can only be a starting point, since good intuition comes from hard work, not from learning the right metaphor. Anyone who reads and understands all of it will still have an arduous journey ahead—but sometimes a good starting point makes a big difference.

It should be noted that this is not a Haskell tutorial; it is assumed that the reader is already familiar with the basics of Haskell, including the standard Prelude, the type system, data types, and type classes.

The type classes we will be discussing and their interrelationships (source code for this graph can be found here):

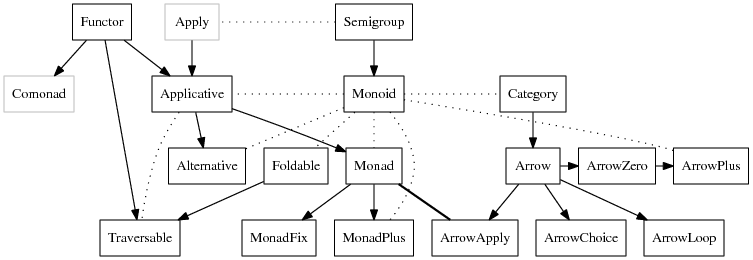
∗ Apply can be found in the semigroupoidspackage, and Comonad in the comonad package.

• Solid arrows point from the general to the specific; that is, if there is an arrow from Foo to Bar it means that every Bar is (or should be, or can be made into) a Foo.
• Dotted lines indicate some other sort of relationship.
• Monad and ArrowApply are equivalent.
• Apply and Comonad are greyed out since they are not actually (yet?) in the standard Haskell libraries ∗.

One more note before we begin. The original spelling of “type class” is with two words, as evidenced by, for example, the Haskell 2010 Language Report, early papers on type classes like Type classes in Haskell and Type classes: exploring the design space, and Hudak et al.’s history of Haskell. However, as often happens with two-word phrases that see a lot of use, it has started to show up as one word (“typeclass”) or, rarely, hyphenated (“type-class”). When wearing my prescriptivist hat, I prefer “type class”, but realize (after changing into my descriptivist hat) that there's probably not much I can do about it.

We now begin with the simplest type class of all: Functor.

3 Functor

The Functor class (haddock) is the most basic and ubiquitous type class in the Haskell libraries. A simple intuition is that a Functor represents a “container” of some sort, along with the ability to apply a function uniformly to every element in the container. For example, a list is a container of elements, and we can apply a function to every element of a list, using map. As another example, a binary tree is also a container of elements, and it’s not hard to come up with a way to recursively apply a function to every element in a tree.

Another intuition is that a Functor represents some sort of “computational context”. This intuition is generally more useful, but is more difficult to explain, precisely because it is so general. Some examples later should help to clarify the Functor-as-context point of view.

In the end, however, a Functor is simply what it is defined to be; doubtless there are many examples of Functor instances that don’t exactly fit either of the above intuitions. The wise student will focus their attention on definitions and examples, without leaning too heavily on any particular metaphor. Intuition will come, in time, on its own.

3.1 Definition

Here is the type class declaration for Functor:

 

Functor is exported by the Prelude, so no special imports are needed to use it. Note that the (<$) operator is provided for convenience, with a default implementation in terms of fmap; it is included in the class just to give Functor instances the opportunity to provide a more efficient implementation than the default. To understand Functor, then, we really need to understand fmap.

First, the f a and f b in the type signature for fmap tell us that f isn’t a concrete type like Int; it is a sort of type function which takes another type as a parameter. More precisely, the kind of f must be * -> *. For example, Maybe is such a type with kind * -> *: Maybe is not a concrete type by itself (that is, there are no values of type Maybe), but requires another type as a parameter, like Maybe Integer. So it would not make sense to say instance Functor Integer, but it could make sense to say instance Functor Maybe.

Now look at the type of fmap: it takes any function from a to b, and a value of type f a, and outputs a value of type f b. From the container point of view, the intention is that fmap applies a function to each element of a container, without altering the structure of the container. From the context point of view, the intention is that fmap applies a function to a value without altering its context. Let’s look at a few specific examples.

Finally, we can understand (<$): instead of applying a function to the values a container/context, it simply replaces them with a given value. This is the same as applying a constant function, so (<$) can be implemented in terms of fmap.

3.2 Instances

∗ Recall that [] has two meanings in Haskell: it can either stand for the empty list, or, as here, it can represent the list type constructor (pronounced “list-of”). In other words, the type [a] (list-of-a) can also be written [] a.

∗ You might ask why we need a separate mapfunction. Why not just do away with the current list-only map function, and rename fmap to mapinstead? Well, that’s a good question. The usual argument is that someone just learning Haskell, when using map incorrectly, would much rather see an error about lists than about Functors.

As noted before, the list constructor [] is a functor ∗; we can use the standard list function map to apply a function to each element of a list ∗. The Maybe type constructor is also a functor, representing a container which might hold a single element. The function fmap g has no effect on Nothing(there are no elements to which g can be applied), and simply applies g to the single element inside a Just. Alternatively, under the context interpretation, the list functor represents a context of nondeterministic choice; that is, a list can be thought of as representing a single value which is nondeterministically chosen from among several possibilities (the elements of the list). Likewise, the Maybe functor represents a context with possible failure. These instances are:

 

As an aside, in idiomatic Haskell code you will often see the letter f used to stand for both an arbitrary Functor and an arbitrary function. In this document, f represents only Functors, and g or h always represent functions, but you should be aware of the potential confusion. In practice, what f stands for should always be clear from the context, by noting whether it is part of a type or part of the code.

There are other Functor instances in the standard library as well:

• Either e is an instance of Functor; Either e a represents a container which can contain either a value of type a, or a value of type e (often representing some sort of error condition). It is similar to Maybe in that it represents possible failure, but it can carry some extra information about the failure as well.

• ((,) e) represents a container which holds an “annotation” of type e along with the actual value it holds. It might be clearer to write it as (e,), by analogy with an operator section like (1+), but that syntax is not allowed in types (although it is allowed in expressions with the TupleSections extension enabled). However, you can certainly think of it as (e,).

• ((->) e) (which can be thought of as (e ->); see above), the type of functions which take a value of type e as a parameter, is a Functor. As a container, (e -> a) represents a (possibly infinite) set of values of a, indexed by values of e. Alternatively, and more usefully, ((->) e) can be thought of as a context in which a value of type e is available to be consulted in a read-only fashion. This is also why ((->) e) is sometimes referred to as the reader monad; more on this later.

• IO is a Functor; a value of type IO a represents a computation producing a value of type a which may have I/O effects. If m computes the value x while producing some I/O effects, then fmap g m will compute the value g x while producing the same I/O effects.

• Many standard types from the containers library (such as Tree, Map, and Sequence) are instances of Functor. A notable exception is Set, which cannot be made a Functor in Haskell (although it is certainly a mathematical functor) since it requires an Ord constraint on its elements; fmap must be applicable to any types a and b. However, Set (and other similarly restricted data types) can be made an instance of a suitable generalization of Functor, either by making a and b arguments to the Functor type class themselves, or by adding an associated constraint.

Exercises

1. Implement Functor instances for Either e and ((->) e).
2. Implement Functor instances for ((,) e) and for Pair, defined as 

   data Pair a = Pair a a

   Explain their similarities and differences.

3. Implement a Functor instance for the type ITree, defined as

   data ITree a = Leaf (Int -> a)
                | Node [ITree a]

4. Give an example of a type of kind * -> * which cannot be made an instance of Functor (without using undefined).
5. Is this statement true or false? 

   The composition of two Functors is also a Functor.

   If false, give a counterexample; if true, prove it by exhibiting some appropriate Haskell code.

3.3 Laws

As far as the Haskell language itself is concerned, the only requirement to be a Functor is an implementation of fmap with the proper type. Any sensible Functor instance, however, will also satisfy the functor laws, which are part of the definition of a mathematical functor. There are two:

 

∗ Technically, these laws make f and fmap together an endofunctor on Hask, the category of Haskell types (ignoring ⊥, which is a party pooper). See Wikibook: Category theory.

Together, these laws ensure that fmap g does not change the structure of a container, only the elements. Equivalently, and more simply, they ensure that fmap g changes a value without altering its context ∗.

The first law says that mapping the identity function over every item in a container has no effect. The second says that mapping a composition of two functions over every item in a container is the same as first mapping one function, and then mapping the other.

As an example, the following code is a “valid” instance of Functor (it typechecks), but it violates the functor laws. Do you see why?

 

Any Haskeller worth their salt would reject this code as a gruesome abomination.

Unlike some other type classes we will encounter, a given type has at most one valid instance of Functor. This can be proven via the free theorem for the type of fmap. In fact, GHC can automatically derive Functorinstances for many data types.

∗ Actually, if seq/undefinedare considered, it is possible to have an implementation which satisfies the first law but not the second. The rest of the comments in this section should be considered in a context where seq and undefinedare excluded.

A similar argument also shows that any Functor instance satisfying the first law (fmap id = id) will automatically satisfy the second law as well. Practically, this means that only the first law needs to be checked (usually by a very straightforward induction) to ensure that a Functor instance is valid.∗

Exercises

1. Although it is not possible for a Functor instance to satisfy the first Functor law but not the second (excluding undefined), the reverse is possible. Give an example of a (bogus) Functor instance which satisfies the second law but not the first.
2. Which laws are violated by the evil Functor instance for list shown above: both laws, or the first law alone? Give specific counterexamples.

3.4 Intuition

There are two fundamental ways to think about fmap. The first has already been mentioned: it takes two parameters, a function and a container, and applies the function “inside” the container, producing a new container. Alternately, we can think of fmap as applying a function to a value in a context (without altering the context).

Just like all other Haskell functions of “more than one parameter”, however, fmap is actually curried: it does not really take two parameters, but takes a single parameter and returns a function. For emphasis, we can write fmap’s type with extra parentheses: fmap :: (a -> b) -> (f a -> f b). Written in this form, it is apparent that fmap transforms a “normal” function (g :: a -> b) into one which operates over containers/contexts (fmap g :: f a -> f b). This transformation is often referred to as a lift; fmap “lifts” a function from the “normal world” into the “f world”.

3.5 Utility functions

There are a few more Functor-related functions which can be imported from the Data.Functor module.

• (<$>) is defined as a synonym for fmap. This enables a nice infix style that mirrors the ($) operator for function application. For example, f $ 3 applies the function f to 3, whereas f <$> [1,2,3] applies fto each member of the list.
• ($>) :: Functor f => f a -> b -> f b is just flip (<$), and can occasionally be useful. To keep them straight, you can remember that (<$) and ($>) point towards the value that will be kept.
• void :: Functor f => f a -> f () is a specialization of (<$), that is, void x = () <$ x. This can be used in cases where a computation computes some value but the value should be ignored.

3.6 Further reading

A good starting point for reading about the category theory behind the concept of a functor is the excellent Haskell wikibook page on category theory.

4 Applicative

A somewhat newer addition to the pantheon of standard Haskell type classes, applicative functorsrepresent an abstraction lying in between Functor and Monad in expressivity, first described by McBride and Paterson. The title of their classic paper, Applicative Programming with Effects, gives a hint at the intended intuition behind the Applicative type class. It encapsulates certain sorts of “effectful” computations in a functionally pure way, and encourages an “applicative” programming style. Exactly what these things mean will be seen later.

4.1 Definition

Recall that Functor allows us to lift a “normal” function to a function on computational contexts. But fmapdoesn’t allow us to apply a function which is itself in a context to a value in a context. Applicative gives us just such a tool, (<*>) (variously pronounced as "apply", "app", or "splat"). It also provides a method, pure, for embedding values in a default, “effect free” context. Here is the type class declaration for Applicative, as defined in Control.Applicative:

 

Note that every Applicative must also be a Functor. In fact, as we will see, fmap can be implemented using the Applicative methods, so every Applicative is a functor whether we like it or not; the Functor constraint forces us to be honest.

(*>) and (<*) are provided for convenience, in case a particular instance of Applicative can provide more efficient implementations, but they are provided with default implementations. For more on these operators, see the section on Utility functions below.

∗ Recall that ($) is just function application: f $ x = f x.

As always, it’s crucial to understand the type signatures. First, consider (<*>): the best way of thinking about it comes from noting that the type of (<*>) is similar to the type of ($) ∗, but with everything enclosed in an f. In other words, (<*>) is just function application within a computational context. The type of (<*>) is also very similar to the type of fmap; the only difference is that the first parameter is f (a -> b), a function in a context, instead of a “normal” function (a

https://wiki.haskell.org/Typeclassopedia