BZOJ 4373算术天才⑨与等差数列(线段树）

题意：
给你一个长度为n的序列，有m个操作，写一个程序支持以下两个操作：

1. 修改一个值

2. 给出三个数l,r,k，

询问：如果把区间[l,r]的数从小到大排序，能否形成公差为k的等差数列。
n,m≤300000 0≤k,a[i]≤10⁹

题解

这题坑我很久。

一眼望去这题不可作。（倒是想到维护最小值和最大值。）

然后翻了题解。发现我的想法和题解差不多。

直接维护区间等差数列显然很难，那么考虑一下：如果区间[l,r] (l < r)排序后能形成公差为k(k>0)的等差数列，要满足什么条件？

1. 很显然，假设min是区间最小值，max是区间最大值，那么 min+k(r−l)=max

2. 区间相邻两个数之差的绝对值的gcd=k

3. 区间没有重复的数

前两个条件 线段树直接维护就好

第三个条件：

对于每个权值开个set，值为位置（离散化标号）

然后维护一个pre[i]，表示当前a[i]这个值，在i前面最后一次出现的位置。那么满足第3个条件，当且仅当区间[l,r]的pre的最大值小于l。这个也是用线段树维护。

然后看修改操作：在set上找前一个数、后一个数，然后修改相应的值

---

然后发现不会用set求前驱后继。然后花了几个小时学。

（一开始翻的博客都只介绍set的函数。然后翻到一篇讲求前去后继的，一眼扫完就会了，看好博客是多么重要啊）

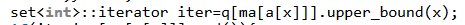
然后这个iter是个迭代器。*iter是第一个比x大的数的实际下标，也就是后继的下标（如果iter是q.end()说明没有后继)

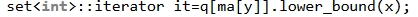
然后这个it也是个迭代器。*it是第一个大于等于x的数的实际下标。然后it--不是减实际的下标，而是使set中的下标。

假如*it是第一个比x小的数的下标，it--后*it就是第二个比x小的数的实际下标。

所以把x插入set后用上面的式子求出it，it--后*it就是x的前驱的实际下标

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #include<set>
 #include<map>
 using namespace std;
 const int N=;
 set<int>q[N<<];
 map<int,int> ma;
 int a[N],pre[N],n,m,num,cnt;
 int gcd(int x,int y){
     if(y==)return x;
     if(x==)return y;
     else return gcd(y,x%y);
 }
 struct tree{
     int l,r,mx,mn,gc,mnp,ln,rn;
 }tr[N<<];
 void update(int now){
     tr[now].ln=tr[now*].ln;
     tr[now].rn=tr[now*+].rn;
     tr[now].gc=abs(tr[now*].rn-tr[now*+].ln);
     tr[now].gc=gcd(tr[now].gc,gcd(tr[now*].gc,tr[now*+].gc));
     tr[now].mn=min(tr[now*].mn,tr[now*+].mn);
     tr[now].mx=max(tr[now*].mx,tr[now*+].mx);
     tr[now].mnp=max(tr[now*].mnp,tr[now*+].mnp);
 }
 void build(int l,int r,int now){
     tr[now].l=l;tr[now].r=r;
     if(l==r){
         tr[now].mx=tr[now].mn=tr[now].ln=tr[now].rn=a[l];
         tr[now].mnp=pre[l];
         return;
     }
     int mid=(tr[now].l+tr[now].r)>>;
     build(l,mid,now*);
     build(mid+,r,now*+);
     update(now);
 }
 void change(int x,int now){
     if(tr[now].l==tr[now].r){
         tr[now].mx=tr[now].mn=tr[now].ln=tr[now].rn=a[tr[now].l];
         tr[now].mnp=pre[tr[now].l];
         return;
     }
     int mid=(tr[now].l+tr[now].r)>>;
     if(x>mid)change(x,now*+);
     else change(x,now*);
     update(now);
 }
 int getmin(int l,int r,int now){
     if(tr[now].l==l&&tr[now].r==r){
         return tr[now].mn;
     }
     int mid=(tr[now].l+tr[now].r)>>;
     if(l>mid)return getmin(l,r,now*+);
     else if(r<=mid)return getmin(l,r,now*);
     else {
         return min(getmin(l,mid,now*),getmin(mid+,r,now*+));
     }
 }
 int getmax(int l,int r,int now){
     if(tr[now].l==l&&tr[now].r==r){
         return tr[now].mx;
     }
     int mid=(tr[now].l+tr[now].r)>>;
     if(l>mid)return getmax(l,r,now*+);
     else if(r<=mid)return getmax(l,r,now*);
     else {
         return max(getmax(l,mid,now*),getmax(mid+,r,now*+));
     }
 }
 int getgcd(int l,int r,int now){
     if(tr[now].l==l&&tr[now].r==r){
         return tr[now].gc;
     }
     int mid=(tr[now].l+tr[now].r)>>;
     if(l>mid)return getgcd(l,r,now*+);
     else if(r<=mid)return getgcd(l,r,now*);
     else {
         return gcd(gcd(getgcd(l,mid,now*),getgcd(mid+,r,now*+)),abs(tr[now*].rn-tr[now*+].ln));
     }
 }
 int getpre(int l,int r,int now){
     if(tr[now].l==l&&tr[now].r==r){
         return tr[now].mnp;
     }
     int mid=(tr[now].l+tr[now].r)>>;
     if(l>mid)return getpre(l,r,now*+);
     else if(r<=mid)return getpre(l,r,now*);
     else {
         return max(getpre(l,mid,now*),getpre(mid+,r,now*+));
     }
 }
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++){
         scanf("%d",&a[i]);
         if(ma[a[i]]==){
             ma[a[i]]=++num;
             q[ma[a[i]]].insert(i);
         }
         else{
             q[ma[a[i]]].insert(i);
             set<int>::iterator it=q[ma[a[i]]].lower_bound(i);
             it--;
             pre[i]=*it;
         }
     }
     build(,n,);
     for(int i=;i<=m;i++){
         int k;
         scanf("%d",&k);
         if(k==){
             int x,y;
             scanf("%d%d",&x,&y);
             x^=cnt;y^=cnt;
             set<int>::iterator iter=q[ma[a[x]]].upper_bound(x);
             if(iter!=q[ma[a[x]]].end()){
                 pre[*iter]=pre[x];
                 change(*iter,);
             }
             q[ma[a[x]]].erase(x);
             a[x]=y;
             if(ma[y]==){
                 ma[y]=++num;
                 q[ma[y]].insert(x);
                 pre[x]=;
             }
             else{
                 q[ma[y]].insert(x);
                 set<int>::iterator it=q[ma[y]].lower_bound(x);
                 if(it!=q[ma[y]].begin()){
                     it--;
                     pre[i]=*it;
                 }
                 iter=q[ma[y]].upper_bound(x);
                 if(iter!=q[ma[y]].end()){
                     pre[*iter]=x;
                     change(*iter,);
                 }
             }
             change(x,);
         }
         else{
             int l;int r;int x;
             scanf("%d%d%d",&l,&r,&x);
             l^=cnt;r^=cnt;x^=cnt;
             int mn=getmin(l,r,);
             int mx=getmax(l,r,);
             if(l==r){
                 printf("Yes\n");
                 cnt++;
                 continue;
             }
             if(x==){
                 if(mn==mx){
                     printf("Yes\n");
                     cnt++;
                 }
                 else printf("No\n");
                 continue;
             }
             if(mn+(r-l)*x!=mx){
                 printf("No\n");
                 continue;
             }
             int GCD=getgcd(l,r,);
             if(GCD%x!=){
                 printf("No\n");
                 continue;
             }
             int PRE=getpre(l,r,);
             if(PRE>=l){
                 printf("No\n");
                 continue;
             }
             printf("Yes\n");
             cnt++;
         }
     }
     return ;
 }