国庆 day 3 上午

a
【问题描述】
　　　　　　　　你是能看到第一题的 friends 呢。
　　　　　　　　　　　　　　　　　　　　　　　　——hja
　　　　怎么快速记单词呢？也许把单词分类再记单词是个不错的选择。何大爷给
　　出了一种分单词的方法，何大爷认为两个单词是同一类的当这两个单词的各个
　　字母的个数是一样的，如 dog 和 god。现在何大爷给了你?个单词，问这里总共
　　有多少类单词。
【输入格式】
　　第一行一个整数n代表单词的个数。
　　接下来n行每行一个单词。
【输出格式】
　　一行一个整数代表答案。
【样例输入】
　　3
　　AABAC
　　CBAAA
　　AAABB
【样例输出】
　　2
【数据范围与规定】
　　70%的数据，1 ≤ ? ≤ 100。
　　对于100%的数据，1 ≤ ? ≤ 10000，所有单词由大写字母组成。
　　P99 zhxb

思路：很简单，sort一下，set记录就好。

#include<set>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n;
string s;
set<string>s1;
using namespace std;
int main(){
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    cin>>n;
    for(int i=;i<=n;i++){
        cin>>s;
        sort(s.begin(),s.end());
        s1.insert(s);
    }
    cout<<s1.size();
}

b
【问题描述】
　　　　　　你是能看到第二题的 friends 呢。
　　　　　　　　　　　　　　　　　　　　　　——laekov
　　　　长度为?的铁丝，你可以将其分成若干段，并把每段都折成一个三角形。你
　　还需要保证三角形的边长都是正整数并且三角形两两相似，问有多少种不同的
　　分法。
【输入格式】
　　一行一个整数n。
【输出格式】
　　一行一个整数代表答案对10 9 + 7取模之后的值。
【样例输入 1
　　6
【样例输出 1】
　　2
【样例输入 2】
　　9
【样例输出 2】
　　6
【样例解释 2】
　　(1,1,1),(2,2,2);(2,2,2),(1,1,1)算两种方案。
【数据范围与规定】
　　对于30%的数据，1≤n≤100。
　　对于60%的数据，1 ≤n≤ 1000。
　　对于100%的数据，1 ≤ n≤ 10^6 。
　　P99 zhxc

思路：打表+

以下解题思路转自xxy大佬的博客

设分成的每段长为Li，g=gcd（Li）

那么一共有n/g 个单位

设f[g]表示以g为周长，且三边gcd为1 的三角形的个数

设h[n/g]表示把n/g个单位 分配给任意多个三角形的个数

那么 ans=Σ f[g]*h[n/g]   （g|n）

求f[g]：

设g=a+b+c，且a<=b<=c

对b和c的大小分两种情况讨论：

① b==c ：

==> g=a+2b，那么b∈[ceil(g/3),floor((g-1)/2)]

所以f[g]=floor((g-1)/2）- ceil(g/3) +1

② b<c ：

a，b，c 的每一种方案都可以看做由 a，b，c-1的每一种方案转移过来

但有一种除外：a+b=c，因为此时a，b，c-1 合法，a，b，c 不合法

当g为偶数时，a+b+a+b=g，g=2*（a+b），所以有floor（g/4）个

所以f[g]=f[g-1]+ （b&1）？ 0 ： -g/4

然后因为要求三边长互质，所以枚举g的每个因数k，f[g]-=f[k]

求h[i]：

把i个物品分成任意份的方案数=C（i-1,0）+C（i-1，1）+……+C（i-1，i-1）

= 2^(i-1)

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 1000010
#define mod 1000000007
using namespace std;
int n,ans;
int f[MAXN],dp[MAXN],more[MAXN];
void pre(){
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
    f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;f[]=;
}
void work(){
    dp[]=;
    for(int i=;i<=n;i++){
        dp[i]=dp[i-]+(i-)/-i/+(i%?:);
        if(i%==)    dp[i]-=i/;
        dp[i]%=mod;
        if(dp[i]<)    dp[i]+=mod;
    }
    more[]=;
    for(int i=;i<=n;i++){
        more[i]=(more[i-]*)%mod;
        for(int j=;i*j<=n;j++){
            dp[i*j]-=dp[i];
            if(dp[i*j]<)    dp[i*j]+=mod;
        }
    }
    return ;
}
int main(){
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    pre();
    scanf("%d",&n);
    if(n<=){
        cout<<f[n];
        return ;
    }
    else{
        work();
        for(int i=;i*i<=n;i++){
            if(n%i!=)    continue;
            ans=(ans+1ll*dp[i]*more[n/i])%mod;
            if(i*i!=n)
                ans=(ans+1ll*dp[n/i]*more[i])%mod;
        }
        cout<<ans;
    }
}

c
【问题描述】
　　　　　　你是能看到第三题的 friends 呢。
　　　　　　　　　　　　　　　　　　　　　　——aoao
　　　　在小学的时候，我们都学过正视图和左视图。现在何大爷用一些小方块摆了
　　一个图形，并给出了你这个图形的左视图和正视图。现在何大爷希望知道，在给
　　定正视图和左视图的情况下，原来的立体图形有多少种可能的情况？
【输入格式】
　　第一行两个整数n,m，代表在左视图和正视图中分别有多少列。
　　第二n个整数，代表在左视图中从左至右每一列的高度。
　　第三行m个整数，代表在正视图中从左至有每一列的高度。
【输出格式】
　　一行一个整数代表答案对10 ⁹ + 9取模之后的值。
【样例输入 1】
　　2 2
　　1 1
　　1 1
【样例输出 1】
　　7
【样例输入 2】
　　4 5
　　5 2 4 1
　　5 2 4 0 1
【样例输出 2】
　　429287
【数据规模与约定】
　　对于20%的数据，1 ≤ n,m ≤ 5，每列的最大高度不超过5。
　　对于40%的数据，n + m ≤ 18。
　　对于100%的数据，1 ≤ n,m ≤ 50，每列最大高度不超过10000。

以下解题思路转自xxy大佬的博客

思路：容斥原理

解决本题的关键：行交换。列交换对答案不影响

将左视图按从下往上递减，正视图从左往右递减排列

那整张图的高度从左下到右上呈阶梯状递减

这样所有高度相同的呈现倒‘L’形，如下图所示蓝色部分

如果我们按高度递减的顺序依次计算每个倒‘L’形的方案数，那么这些倒‘L’形相对独立

答案就是所有倒‘L’形答案的乘积

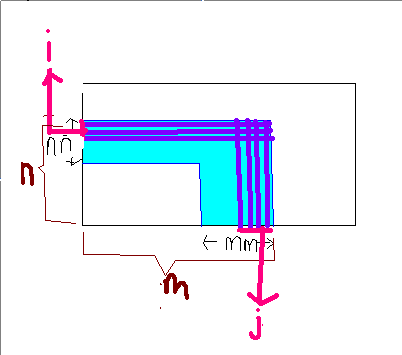
如何计算单个倒‘L’形的答案？——容斥原理

假设上图为已经按高度排好序的图

设当前正在处理高度为h的倒‘L’形

令nn表示当前有nn行的左视图高度为h，mm表示当前有mm列的主视图高度为h

n表示当前有n行的左视图高度>=h，m表示当前有m列的主视图高度>=h

定义性质pk表示 在这nn行mm列中，有k行/列不满足看到的高度为h

那根据容斥原理，

不具有任何一个性质p的方案和=

全集-Σ|pi|+Σ|pi∩pj|-Σ|pi∩pj∩pk|+…+（-1）^m*|p1∩p2∩…∩pm|

也就是所有方案-所有1行/列不满足条件的方案+所有2行/列不满足条件的方案-……

如何求有k行/列不满足条件的方案数？

设现在要求在倒‘L’形中，有i行j列不满足条件的方案数A，i+j=k

那么A分为两部分

① i行j列不能满足条件的部分：

当前高度为h，不能满足条件，每一个各自可以填[0,h-1],每个格子有h种方案

所以此时方案数=h^ （n*m-(n-i)*(m-j)）

② 倒‘L’形中其他位置可以任意填的部分

当前高度为h，任意填就是可以填[0,h]，每个各自有h+1种方案

所以此时的方案数=（h+1）^（(n-i)*(m-j)-(n-nn)*(m-mm)）

这是选定i行j列，所以还要乘上在nn行中选i行，在mm列中选j列的方案

终上所述，每个倒‘L’形 的答案为 （-1）^（i+j）* C（nn，i）* C（mm，j）* h^ （n*m-(n-i)*(m-j)） * （h+1）^（(n-i)*(m-j)-(n-nn)*(m-mm)）

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 10001
#define mod 1000000009
using namespace std;
int n,m;
int c[][];
int a[MAXN],b[MAXN];
void pre(int k){
    for(int i=;i<=k;i++)    c[i][]=;
    for(int i=;i<=k;i++)
        for(int j=;j<=i;j++)
            c[i][j]=(c[i-][j]+c[i-][j-])%mod;
}
int pow(int a,int b){
    int res=;
    for(;b;b>>=,a=1ll*a*a%mod)
        if(b&)    res=1ll*res*a%mod;
    return res;
}
int cal(int n,int m,int nn,int mm,int h){
    int res=,tmp;
    for(int i=;i<=nn;i++)
        for(int j=;j<=mm;j++){
            tmp=1ll*pow(h,n*m-(n-i)*(m-j))*pow(h+,(n-i)*(m-j)-(n-nn)*(m-mm))%mod*c[nn][i]%mod*c[mm][j]%mod;
            if((i+j)&)    res=((res-tmp)%mod+mod)%mod;
            else res+=tmp,res%=mod;
        }
    return res;
}
int main(){
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++){
        int x;
        scanf("%d",&x);
        a[x]++;
    }
    for(int i=;i<=m;i++){
        int x;
        scanf("%d",&x);
        b[x]++;
    }
    pre(max(n,m));
    long long res=;
    int nown=,nowm=;
    for(int i=;i>=;i--)
        if(a[i]||b[i]){
            nown+=a[i];
            nowm+=b[i];
            res=1ll*res*cal(nown,nowm,a[i],b[i],i)%mod;
        }
    cout<<res;
}