[luogu2119]魔法阵 NOIP2016T4

很好的一道数学推导题

45分做法

$O(N^4)$暴力枚举四个材料

55分做法

从第一个约束条件可得到所有可行答案都是单调递增的，所以可以排序一遍，减少枚举量，可以拿到55分

100分做法

首先可以发现每个$x$都小于n，而$n$最大值只是$15000$，所以可以开一个桶来存每个魔法值出现的次数

回忆一下3个约束条件

$xa<xb<xc<xd$ ①

$xb-xa=2(xd-xc)$ ②

$xb-xa<(xc-xb)/3$ ③

现在魔改一下这三个式子

设$t=xd-xc$

所以②可化为$xb-xa=2t$ ④

将④代入③

$2t<(xc-xb)/3$

移项一下，就变成

$6t<xc-xb$ ⑤

再魔改一下

设$6t+k=xc-xb$（就是把差的部分补上去）

于是可以画出来一个图

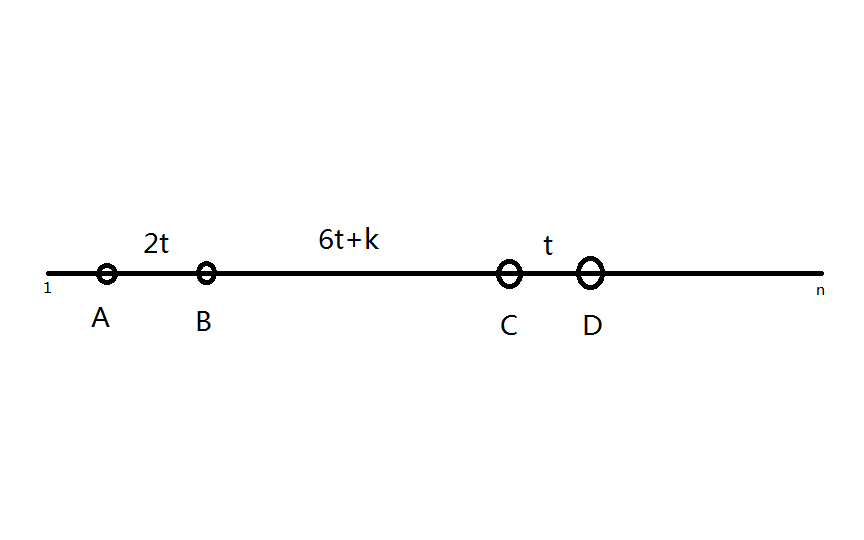
显然，$A$的最小值为$1$，$D$的最大值为$n$

由图可得$AD=9t+k$

所以我们可以尝试着枚举t，用t来表示各个魔法值的值

由上易得t的范围为$1<=t<=(n-1)/9$

在代码中为了避免除法写成$t*9<n$

再枚举D，因为我们已经枚举出了t，所以C的值是可以直接算出来的

$C=D-t$

又因为使$A,B,C,D$满足条件的k的最小值为1，所以对于当前的C和D，最大的A和B为$A=D-9t-1,B=D-7t-1$

那么如果A和B更小怎么办？

观察到在其他条件不变的情况下，只要$C$和$B$满足$Xc-Xb>6t$，那么这个魔法阵就一定成立，所以当$(a1<a2,b1<b2)$时，只要$a2$和$b2$能够和$C,D$组成魔法阵，$a1,b1$也一定能和$C,D$组成魔法阵，所以可以使用前缀和优化

然后又由乘法原理可得，当前魔法值作为$D$物品的个数为$SumD=SumA*SumB*SumC$

所以我们利用前缀和优化$SumA*SumB$

C的情况可以顺便在算D的时候算出来

那么还有一个问题是，我们枚举的D的范围是多少？

因为要统计前缀和，所以一定是要顺推下去的，由上面那张图我们可以知道，D的最大值为n，最小值则为当k=1且A=1的时候，所以D的最小值为$9*t+2$，再小是无法组成魔法阵的

同理可以枚举A

但是这个的情况又和枚举D的情况有一点不同

在其他条件不变的情况下，只要$C$和$B$满足$Xc-Xb>6t$，那么这个魔法阵就一定成立，所以当$(c1<c2,d1<d2)$时，只要$c1$和$d1$能够和$A,B$组成魔法阵，$c2,d2$也一定能和$A,B$组成魔法阵，所以可以使用后缀和优化

因为需要统计后缀和，所以需要逆推

枚举的范围：A的最大值为$(n-t*9-1)$(因为当k=1，D=n的时候A才最大)，A的最小值则为1

所以就可以算出每个魔法值作为$A,B,C,D$物品的次数了，输出时直接输出当前魔法物品的魔法值的次数就可以了

#include <cstdio>
#include <algorithm>
using namespace std;
inline int read(){
    int x=,f=;char c=getchar();
    while(c<''||c>''){if(c=='-')f=-f;c=getchar();}
    while(c>=''&&c<=''){x=(x<<)+(x<<)+c-'';c=getchar();}
    return x*f;
}
#define N 50010
int n,m;
int a[N],b[N],c[N],d[N];
int x[N],vis[N];
int main(){
    n=read();m=read();
    for(int i=;i<=m;i++)
        x[i]=read(),vis[x[i]]++;
    for(int t=;t*<n;t++){
        int sum=;
        for(int D=*t+;D<=n;D++){
            int A=D-*t-;
            int B=A+*t;
            int C=D-t;
            sum+=vis[A]*vis[B];
            c[C]+=vis[D]*sum;
            d[D]+=vis[C]*sum;
        }
        sum=;
        for(int A=n-*t-;A;A--){
            int B=A+*t;
            int C=B+*t+;
            int D=A+*t+;
            sum+=vis[C]*vis[D];
            a[A]+=vis[B]*sum;
            b[B]+=vis[A]*sum;
        }
    }
    for(int i=;i<=m;i++){
        printf("%d %d %d %d\n",a[x[i]],b[x[i]],c[x[i]],d[x[i]]);
    }
    return ;
}

---

参考资料：

学长的博客

（如果看不懂我的题解可以去看一下学长的qwq，我是看他的题解才懂这道题怎么写的，然后自己再归纳总结一下才写出来这篇博客）