B-树 B+树 B*树

区分B树，B-树

有的文章说二叉查找树(Binary Search Tree，BST)就是B树，这个我总结来说是不对的

B树和B-树是同一种树，只不过英语中B-tree被中国人翻译成了B-树，让人以为B树和B-树是两种树，实际上，两者就是同一种树。

前言：

动态查找树主要有：二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced Binary Search Tree），红黑树(Red-Black Tree )，B-tree/B+-tree/ B*-tree (B~Tree)。

前三者是典型的二叉查找树结构，其查找的时间复杂度O(log2N)与树的深度相关，那么降低树的深度自然会提高查找效率。
但是咱们有面对这样一个实际问题：就是大规模数据存储中，实现索引查询这样一个实际背景下，树节点存储的元素数量是有限的（如果元素数量非常多的话，查找就退化成节点内部的线性查找了），这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁，进而导致查询效率低下（为什么会出现这种情况，待会在外部存储器-磁盘中有所解释），那么如何减少树的深度（当然是不能减少查询的数据量），一个基本的想法就是：采用多叉树结构（由于树节点元素数量是有限的，自然该节点的子树数量也就是有限的）。
也就是说，因为磁盘的操作费时费资源，如果过于频繁的多次查找势必效率低下。那么如何提高效率，即如何避免磁盘过于频繁的多次查找呢？根据磁盘查找存取的次数往往由树的高度所决定，所以，只要我们通过某种较好的树结构减少树的结构尽量减少树的高度，那么是不是便能有效减少磁盘查找存取的次数呢？那这种有效的树结构是一种怎样的树呢？
这样我们就提出了一个新的查找树结构——多路查找树。根据平衡二叉树的启发，自然就想到平衡多路查找树结构，也就是这篇文章所要阐述的第一个主题B~tree，即B树结构(后面，我们将看到，B树的各种操作能使B树保持较低的高度，从而达到有效避免磁盘过于频繁的查找存取操作，从而有效提高查找效率)。

B-tree（B-tree树即B树，B即Balanced，平衡的意思），是一种多叉平衡查找树，m阶B树，节点最多含m-1个key，最少含[(m-1)/2]（上取整）个key(阶：节点最多有多少子节点，跟度的意思差不多)

一个m阶的B树具有如下几个特征：
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
3.每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

下图是一个4 阶的B树:

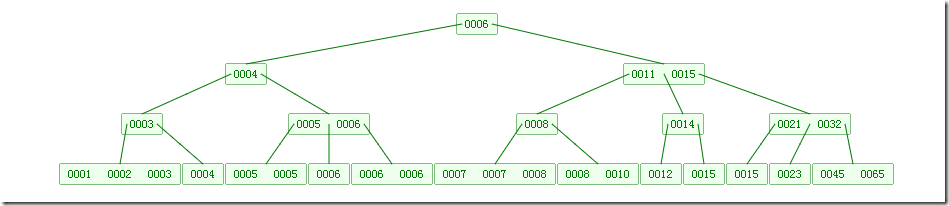
B树的插入及平衡化操作和2-3树很相似。下面是往B树中依次插入

6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4

B+树：（B树的一种变形树）

一个m阶的B+树具有如下几个特征：
1.有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。
2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
3.所有的中间节点元素都同时存在于子节点，元素中是最大（或最小）元素存在与叶子结点中。

如下图，是一个B+树:

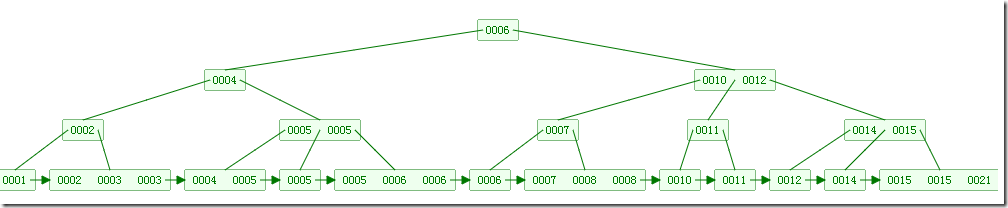
下图是B+树的插入动画：

B+树的优势：
1.单一节点存储更多的元素，使得查询的IO次数更少。(B+树的中间节点没有卫星数据，所以同样大小的磁盘页可以容纳更多的节点元素，这意味着数据量相同的情况下，B+树比B-树更加矮胖，因此查询的io次数也更少)
2.所有查询都要查找到叶子节点，查询性能稳定。(B树只要找到匹配元素即可，无论元素处于中间节点还是叶子节点，最好情况下，只查根节点)
3.所有叶子节点形成有序链表，便于范围查询。(只需链表上做遍历即可)

但是B树也有优点，其优点在于，由于B树的每一个节点都包含key和value，因此经常访问的元素可能离根节点更近，因此访问也更迅速。

下面是B 树和B+树的区别图：

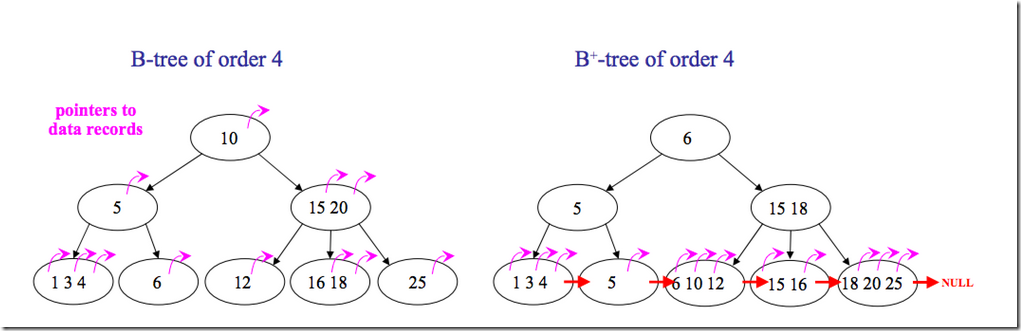
B*树：（B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针）

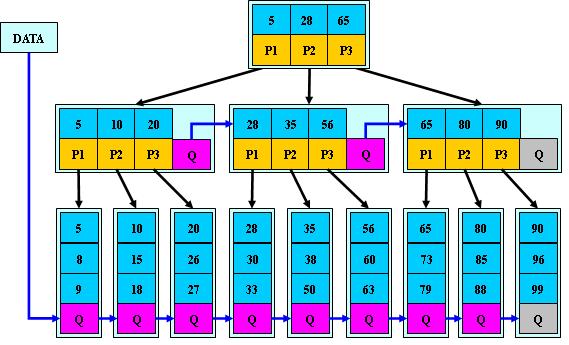
B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；
B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之
  间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；
所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

总结：

为什么现在的数据库索引一般都使用B树，B+树，而不使用二分查找树？

二分查找数查找次数取决于树的高度，B树中的查询次数不比二叉查找树少，特别是一个节点中元素数量很多时，但是要考虑现实使用的数据在磁盘中的存储情况，
一般一个节点都存储在磁盘的一个页中，相较磁盘的io耗时，一个节点内部元素在内存中查找的时间基本忽略，所以只要树的高度足够低，io次数足够少，就可以提升查询性能。

B树：有序数组+平衡多叉树；
B+树：有序数组链表+平衡多叉树；
B*树：一棵丰满的B+树。

看的有的文章说B树，B+树的每个节点至少有ceil(m/2)个孩子（ceil()为向上取整） ，疑问中？

应用：

B树：文件系统，MongoDB数据库索引

B+树：大部分关系型数据库索引（MSSQL,MySQL）

http://blog.csdn.net/v_JULY_v/article/details/6530142

https://www.cnblogs.com/oldhorse/archive/2009/11/16/1604009.html

http://www.cnblogs.com/yangecnu/p/Introduce-B-Tree-and-B-Plus-Tree.html

http://blog.csdn.net/bjweimengshu/article/details/78909127

https://troywu0.gitbooks.io/spark/content/bshu_b_shu.html

http://blog.csdn.net/oxygen0106/article/details/40262829