The algorithm learning of sort which include Bubblesort,Insertsort,Quicksort and Mergesort.

Notice : these algorithms achieved by Java.

So,let's going to it.

firstly, what is Bubblesort? why we call it in this name?

emmmm.... Maybe this image will give you a clear understanding.

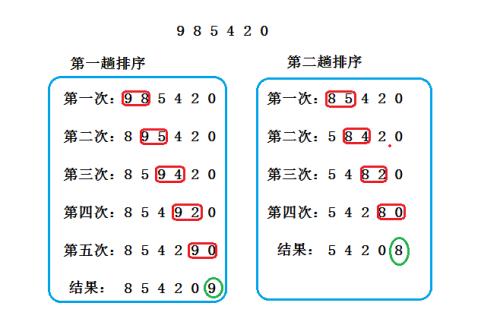
　　　　　　　　　　Bubblesort.jpg

I meet so many descriptions,and they all have a common that is : the key which in sorting will end in it's final position!

Bubblesort is stable

there is code:

import java.util.Arrays;

public class BubbleSort{
    public static void sort(int[] arr){
        for(int i=0;i<arr.length;i++){
            for(int j=0;j<arr.length-i-1;j++){
                if(arr[j]>arr[j+1]){
                    int temp=arr[j+1];
                    arr[j+1]=arr[j];
                    arr[j]=temp;
                }
            }
        }
    }
    public static void main(String [] args){
        int[] ints={5,3,4,1,2};
        sort(ints);
        System.out.println(Arrays.toString(ints));
    }
}

Secondly,about Insertsort

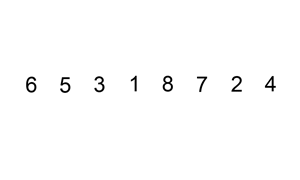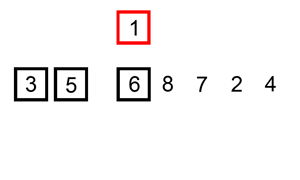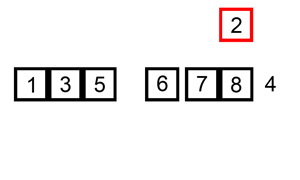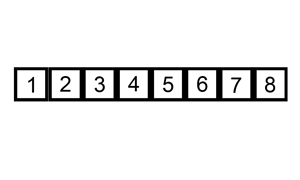
This sorting is find the appropriate position. when a key is low in front ,they will exchange.

code:

import java.util.Arrays;
public class InsertSort{
    public static void sort(int[] arr){
        int temp;
        for(int i=0;i<arr.length;i++){
            for(int j=0;j<i;j++){
                if(arr[i]<arr[j]){

                temp=arr[i];
                arr[i]=arr[j];
                arr[j]=temp;
            }
            }
        }
    }
    public static void main(String [] args){
        int [] ints={5,3,4,1,2};
        sort(ints);
        System.out.println(Arrays.toString(ints));
    }
}

Thirdly,the Mergesort.

1,Request space to be the sum of two sorted sequences, which are used to store merged sequences

2,Set two pointers at the beginning of two sorted sequences

3,Compare the elements pointed by the two pointers, select the relatively small elements and place them in the merge space, and move the pointer to the next location.

4,Repeat step 3 until a pointer reaches the end of the sequence

5,Copy all the remaining elements of another sequence directly to the end of the merged sequence

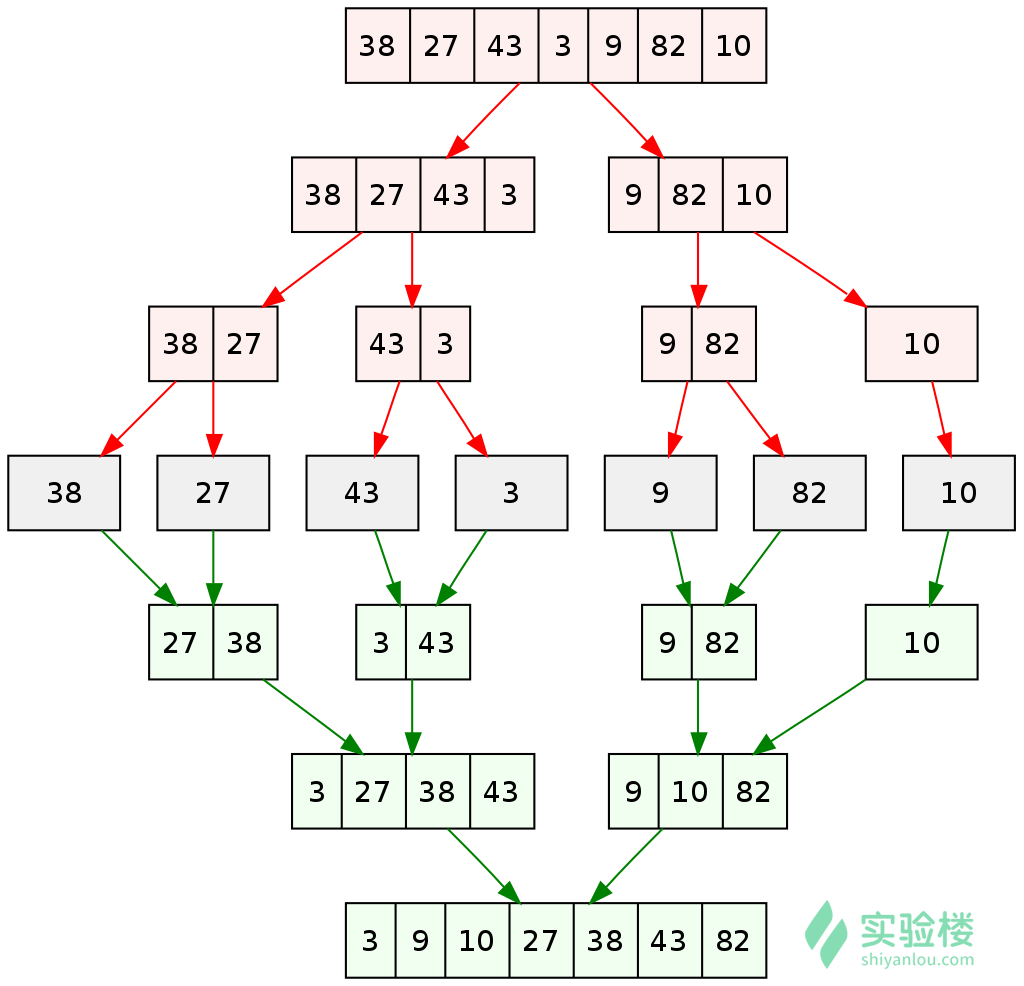
code:

import java.util.Arrays;

public class MergeSort{
    public static void mergeSort(int [] arrays,int left,int right){
  //如果数组还可以拆分
        if(left<right)
        {
            //数组的中间位置
            int middle=(left+right)/2;
            //拆分左边数组
            mergeSort(arrays,left,middle);
            //拆分右边数组
            mergeSort(arrays,middle+1,right);
            //合并
            merge(arrays,left,middle,right);
        }
    }
    /*
        合并数组
    */
    public static void merge(int [] arr,int left,int middle,int right){
        //申请合并空间 大小为两个已经排序序列之和
        int [] temp=new int[right-left+1];
        //i和j为两个已经排序号的数组的起始位置
        int i=left;
        int j=middle+1;
        int k=0;
        while(i<=middle&&j<=right){
            //将比较小的数组放入合并空间
            if(arr[i]<arr[j]){
                temp[k++]=arr[i++];

            }else{
                temp[k++]=arr[j++];
            }
        }
        //将左边剩余元素写入合并空间
        while(i<=middle){
            temp[k++]=arr[i++];

        }
        //将右边剩余元素写入合并空间
        while(j<=right){
            temp[k++]=arr[j++];
        }
        //将排序后的数组协会原来的数组
        for(int l=0;l<temp.length;l++){
            arr[l+left]=temp[l];
        }
    }
    public static void main(String [] args){
        int[] ints={5,3,4,1,2};
        mergeSort(ints,0,ints.length-1);
        System.out.println(Arrays.toString(ints));
    }
}

The most important sorting :Quicksort

Quicksort , also known as partition-exchange sort, is short for Quicksort, a sort algorithm, first proposed by Tony Hall. On average, the order of n items is O (nlogn) times. In the worst case, O (n ^ 2) comparisons are required, but this is not common. In fact, Quick Sorting O (nlogn) is usually significantly faster than other algorithms because its inner loop can be achieved efficiently on most architectures.

step:

Pick out an element from a sequence called pivot.

Rearrange the sequence. All elements smaller than the benchmark are placed in front of the benchmark, and all elements larger than the benchmark are placed behind the benchmark (the same number can go to any side). After this segmentation, the benchmark is in the middle of the sequence. This is called a partition operation.

Recursively, the subordinate sequence of elements smaller than the base value and those larger than the base value is sorted.

code:

import java.util.Arrays;

public class QuickSort{
    public static void sort(int[] arr,int head,int tail){
        if(head>=tail||arr==null||arr.length<=1){
            return;
        }
        //设置数组的起始位置i 结束位置j  基准pivot为数组的中间
        int i=head,j=tail,pivot=arr[(head+tail)/2];
        while(i<=j){
            //当数组小于基准 循环结束后 相当于i所处的位置的值为大于基准的元素
            while(arr[i]<pivot){
                ++i;
            }
            //当数组大于基准  循环结束后 相当于j所处的位置的值为小于基准的元素
            while(arr[j]>pivot){
                --j;
            }
            //如果i<j 那么将交换i j对应位置的值
            if(i<j){
                int t=arr[i];
                arr[i]=arr[j];
                arr[j]=t;
                //指针继续移动
                ++i;
                --j;
            }else if(i==j){
                //如果i=j，那么说明本次排序已经结束，将i++ 如果这里不使用i++ 那么后面的sort（arr，i，tial）将改为sort(arr,i+1,tail)
                ++i;
              }
        }
        //继续将数组分割
            sort(arr,head,j);
            sort(arr,i,tail);
     }

     public static void main(String[] args){
         int[] ints={5,3,4,1,2};
         sort(ints,0,ints.length-1);
         System.out.println(Arrays.toString(ints));
     }
}