啊 B树
关于B树的阶
B树的阶(英语对应order)定义是不统一的:
Unfortunately, the literature on B-trees is not uniform in its terminology (Folk & Zoellick 1992, p. 362).
Bayer & McCreight (1972), Comer (1979), and others define the order of B-tree as the minimum number of keys in a non-root node.
Folk & Zoellick (1992) points out that terminology is ambiguous because the maximum number of keys is not clear. An order 3 B-tree might hold a maximum of 6 keys or a maximum of 7 keys.
Knuth (1998, p. 483) avoids the problem by defining the order to be maximum number of children (which is one more than the maximum number of keys).国内的数据结构教材一般是按照Knuth定义,即“阶”定义为一个节点的子节点数目的最大值。
对于一棵m阶B-tree,每个结点至多可以拥有m个子结点。各结点的关键字和可以拥有的子结点数都有限制,规定m阶B-tree中,根结点至少有2个子结点,除非根结点为叶子节点,相应的,根结点中关键字的个数为1~m-1,比节点数目少一个;非根结点至少有[m/2]([],向上取整)个子结点,相应的,关键字个数为[m/2]-1~m-1。
上面这段引用自 https://darrenzhu.iteye.com/blog/2050087
以下转自 https://www.cnblogs.com/xiaoxi/p/6868087.html
一、零铺垫
在介绍B树之前,先来看另一棵神奇的树——二叉排序树(Binary Sort Tree),首先它是一棵树,“二叉”这个描述已经很明显了,就是树上的一根树枝开两个叉,于是递归下来就是二叉树了(下图所示),而这棵树上的节点是已经排好序的,具体的排序规则如下:
- 若左子树不空,则左子树上所有节点的值均小于它的根节点的值
- 若右子树不空,则右子树上所有节点的值均大于它的根节点的值
- 它的左、右子树也分别为二叉排序数(递归定义)
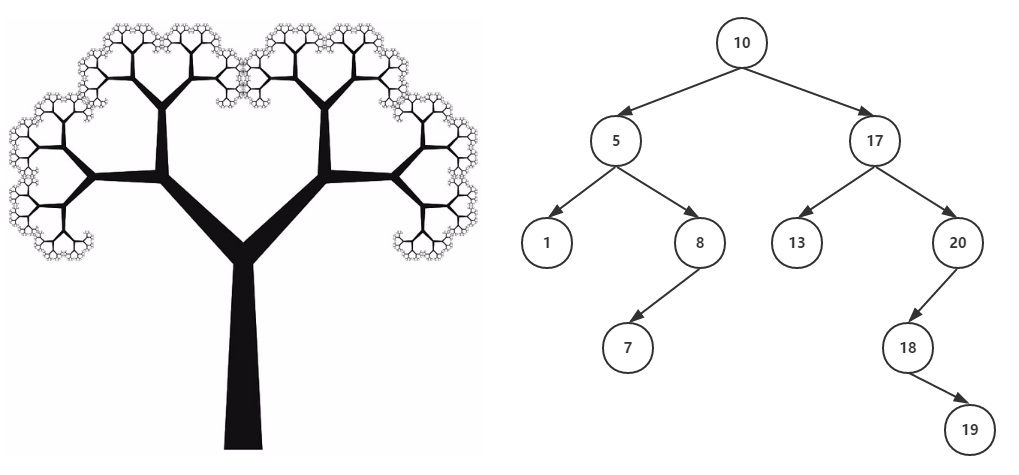
从图中可以看出,二叉排序树组织数据时,用于查找是比较方便的,因为每次经过一次节点时,最多可以减少一半的可能,不过极端情况会出现所有节点都位于同一侧,直观上看就是一条直线,那么这种查询的效率就比较低了,因此需要对二叉树左右子树的高度进行平衡化处理,于是就有了平衡二叉树(Balenced Binary Tree)。
所谓“平衡”,说的是这棵树的各个分支的高度是均匀的,它的左子树和右子树的高度之差绝对值小于1,这样就不会出现一条支路特别长的情况。于是,在这样的平衡树中进行查找时,总共比较节点的次数不超过树的高度,这就确保了查询的效率(时间复杂度为O(logn))。
二、B树的起源
B树,最早是由德国计算机科学家Rudolf Bayer等人于1972年在论文 《Organization and Maintenance of Large Ordered Indexes》提出的,不过我去看了看原文,发现作者也没有解释为什么就叫B-trees了,所以把B树的B,简单地解释为Balanced或者Binary都不是特别严谨,也许作者就是取其名字Bayer的首字母命名的也说不定啊……
三、B树长啥样
还是直接看图比较清楚,图中所示,B树事实上是一种平衡的多叉查找树,也就是说最多可以开m个叉(m>=2),我们称之为m阶b树,为了体现本博客的良心之处,不同于其他地方都能看到2阶B树,这里特意画了一棵5阶B树 。
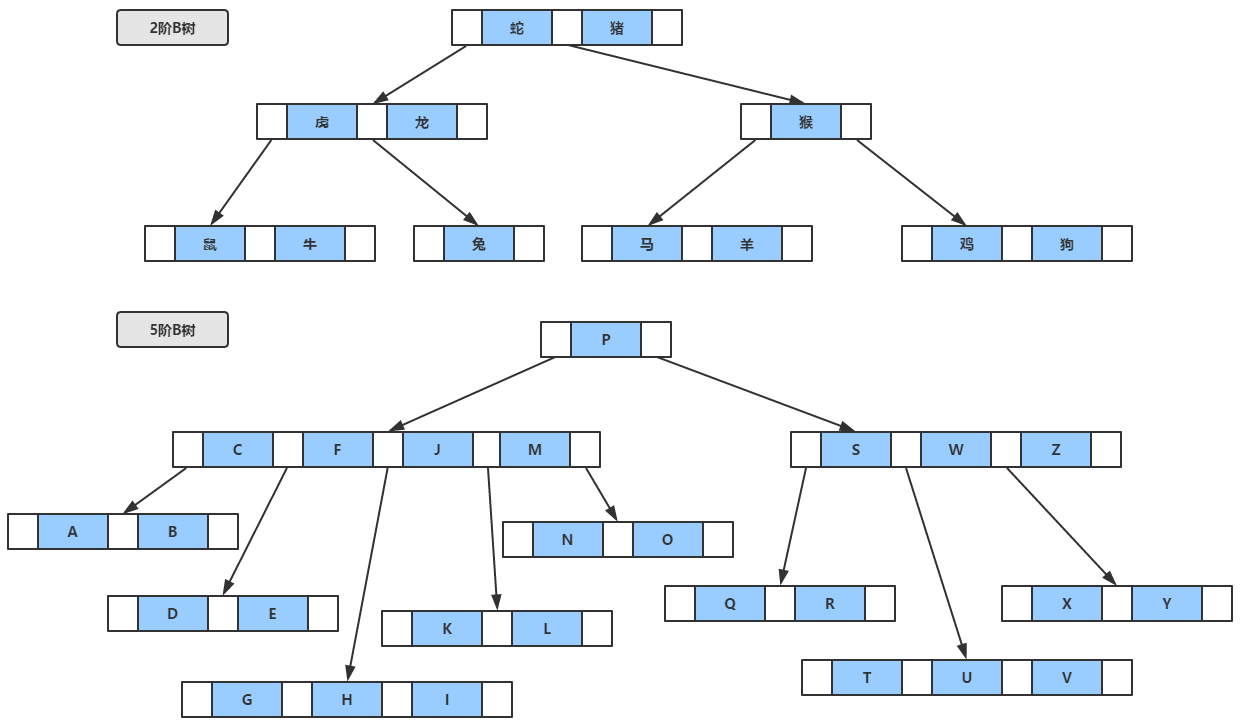
总的来说,m阶B树满足以下条件:
- 每个节点至多可以拥有m棵子树
- 根节点,只有至少有2个节点(要么极端情况,就是一棵树就一个根节点,单细胞生物,即是根,也是叶,也是树)。
- 非根非叶的节点至少有的Ceil(m/2)个子树(Ceil表示向上取整,图中5阶B树,每个节点至少有3个子树,也就是至少有3个叉)。
- 非叶节点中的信息包括[n,A0,K1,A1,K2,A2,…,Kn,An],,其中n表示该节点中保存的关键字个数,K为关键字且Ki<Ki+1,A为指向子树根节点的指针。
- 从根到叶子的每一条路径都有相同的长度,也就是说,叶子节在相同的层,并且这些节点不带信息,实际上这些节点就表示找不到指定的值,也就是指向这些节点的指针为空。
B树的查询过程和二叉排序树比较类似,从根节点依次比较每个结点,因为每个节点中的关键字和左右子树都是有序的,所以只要比较节点中的关键字,或者沿着指针就能很快地找到指定的关键字,如果查找失败,则会返回叶子节点,即空指针。
例如查询图中字母表中的K
- 从根节点P开始,K的位置在P之前,进入左侧指针
- 左子树中,依次比较C、F、J、M,发现K在J和M之间
- 沿着J和M之间的指针,继续访问子树,并依次进行比较,发现第一个关键字K即为指定查找的值
四、Plus版——B+树
作为B树的加强版,B+树与B树的差异在于
- 有n棵子树的节点含有n个关键字(也有认为是n-1个关键字)
- 所有的叶子节点包含了全部的关键字,及指向含这些关键字记录的指针,且叶子节点本身根据关键字自小而大顺序连接
- 非叶子节点可以看成索引部分,节点中仅含有其子树(根节点)中的最大(或最小)关键字
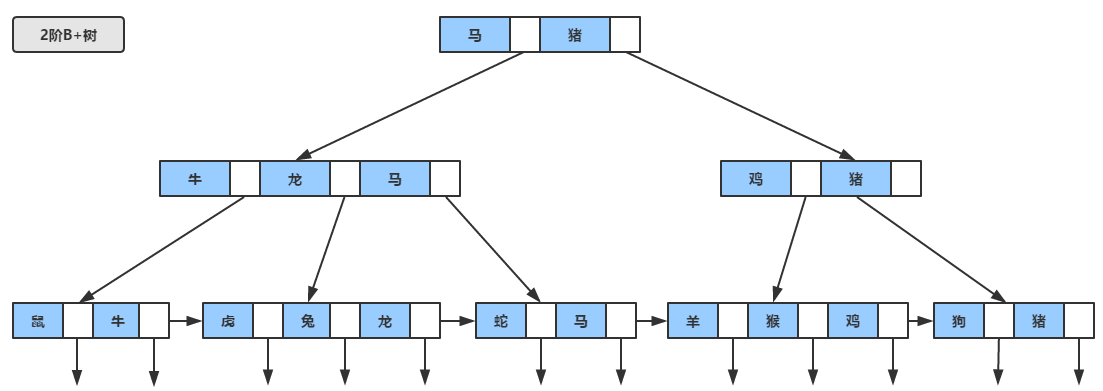
B+树的查找过程,与B树类似,只不过查找时,如果在非叶子节点上的关键字等于给定值,并不终止,而是继续沿着指针直到叶子节点位置。因此在B+树,不管查找成功与否,每次查找都是走了一条从根到叶子节点的路径。
五、MySQL是如何使用B树的
说明:事实上,在MySQL数据库中,诸多存储引擎使用的是B+树,即便其名字看上去是BTREE。
1、innodb的索引机制
先以innodb存储引擎为例,说明innodb引擎是如何利用B+树建立索引的。首先创建一张表:zodiac,并插入一些数据

CREATE TABLE `zodiac` (
`id` int(11) NOT NULL AUTO_INCREMENT,
`name` char(4) NOT NULL,
PRIMARY KEY (`id`),
KEY `index_name` (`name`)
); insert zodiac(id,name) values(1,'鼠');
insert zodiac(id,name) values(2,'牛');
insert zodiac(id,name) values(3,'虎');
insert zodiac(id,name) values(4,'兔');
insert zodiac(id,name) values(5,'龙');
insert zodiac(id,name) values(6,'蛇');
insert zodiac(id,name) values(7,'马');
insert zodiac(id,name) values(8,'羊');
insert zodiac(id,name) values(9,'猴');
insert zodiac(id,name) values(10,'鸡');
insert zodiac(id,name) values(11,'狗');
insert zodiac(id,name) values(12,'猪');

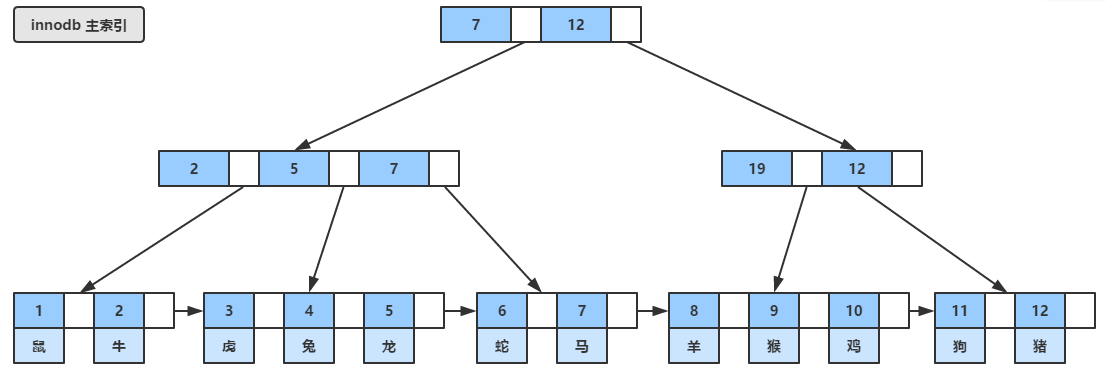
对于innodb来说,只有一个数据文件,这个数据文件本身就是用B+树形式组织,B+树每个节点的关键字就是表的主键,因此innodb的数据文件本身就是主索引文件,如下图所示,主索引中的叶子页(leaf page)包含了数据记录,但非叶子节点只包含了主键,术语“聚簇”表示数据行和相邻的键值紧凑地存储在一起,因此这种索引被称为聚簇索引,或聚集索引。
这种索引方式,可以提高数据访问的速度,因为索引和数据是保存在同一棵B树之中,从聚簇索引中获取数据通常比在非聚簇索引中要来得快。
所以可以说,innodb的数据文件是依靠主键组织起来的,这也就是为什么innodb引擎下创建的表,必须指定主键的原因,如果没有显式指定主键,innodb引擎仍然会对该表隐式地定义一个主键作为聚簇索引。
同样innodb的辅助索引,如下图所示,假设这些字符是按照生肖的顺序排列的(其实我也不知道具体怎么实现,不要在意这些细节,就是举个例子),其叶子节点中也包含了记录的主键,因此innodb引擎在查询辅助索引的时候会查询两次,首先通过辅助索引得到主键值,然后再查询主索引,略微有点啰嗦。。。
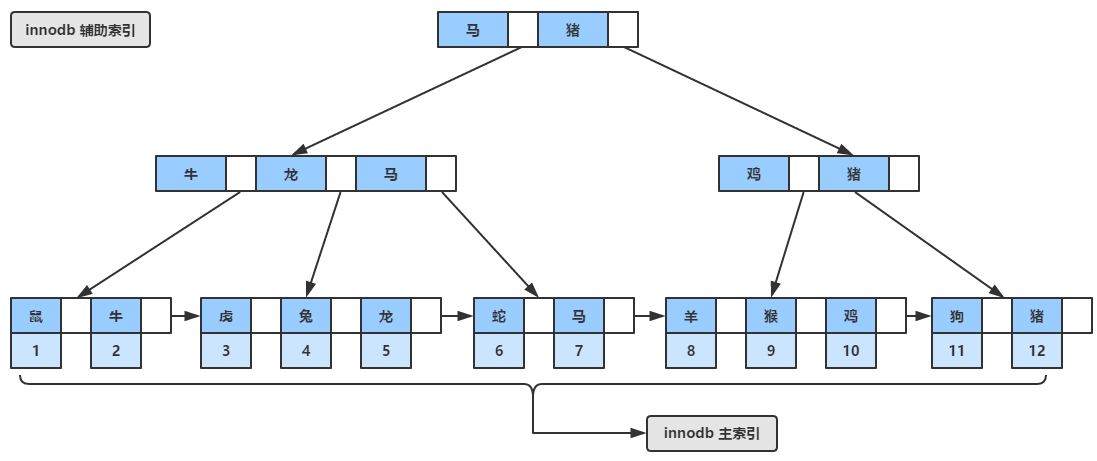
2、MyISAM的索引机制
MyISAM引擎同样也使用B+树组织索引,如下图所示,假设我们的数据不是按照之前的顺序插入的,而是按照图中的是顺序插入表,可以看到MyISAM引擎下,B+树叶子节点中包含的是数据记录的地址(可以简单理解为“行号”),而MyISAM的辅助索引在结构上和主索引没有本质的区别,同样其叶子节点也包含了数据记录的地址,稍微不同的是辅助索引的关键字是允许重复。
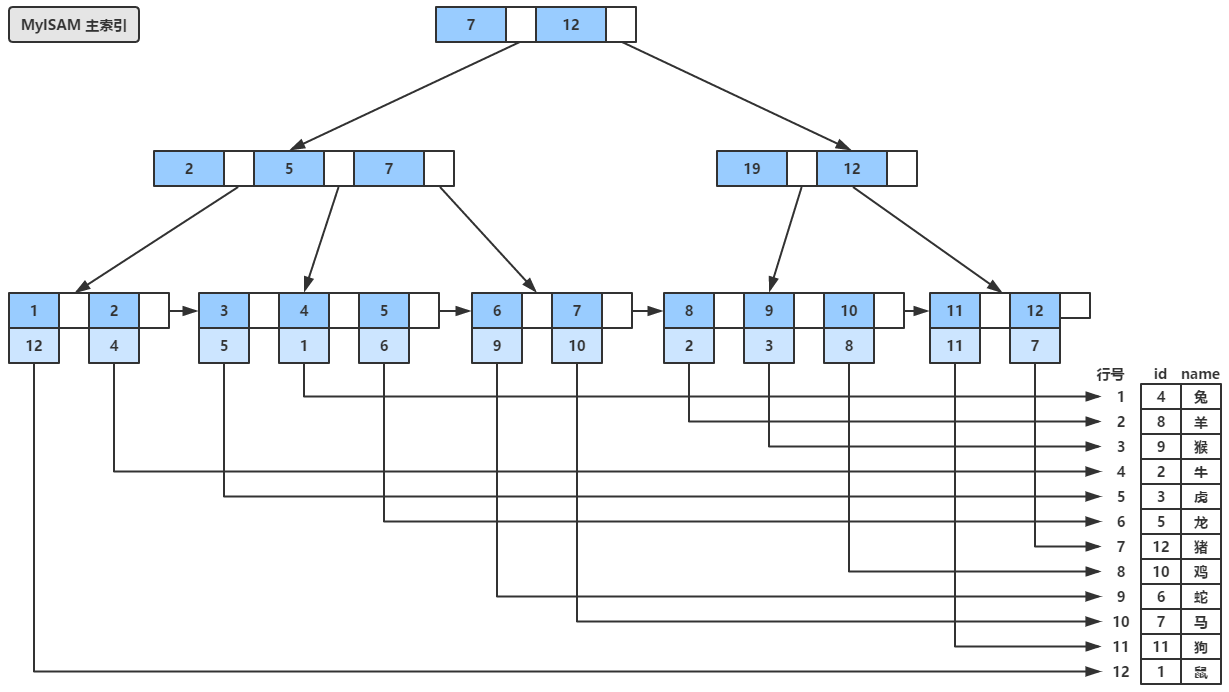
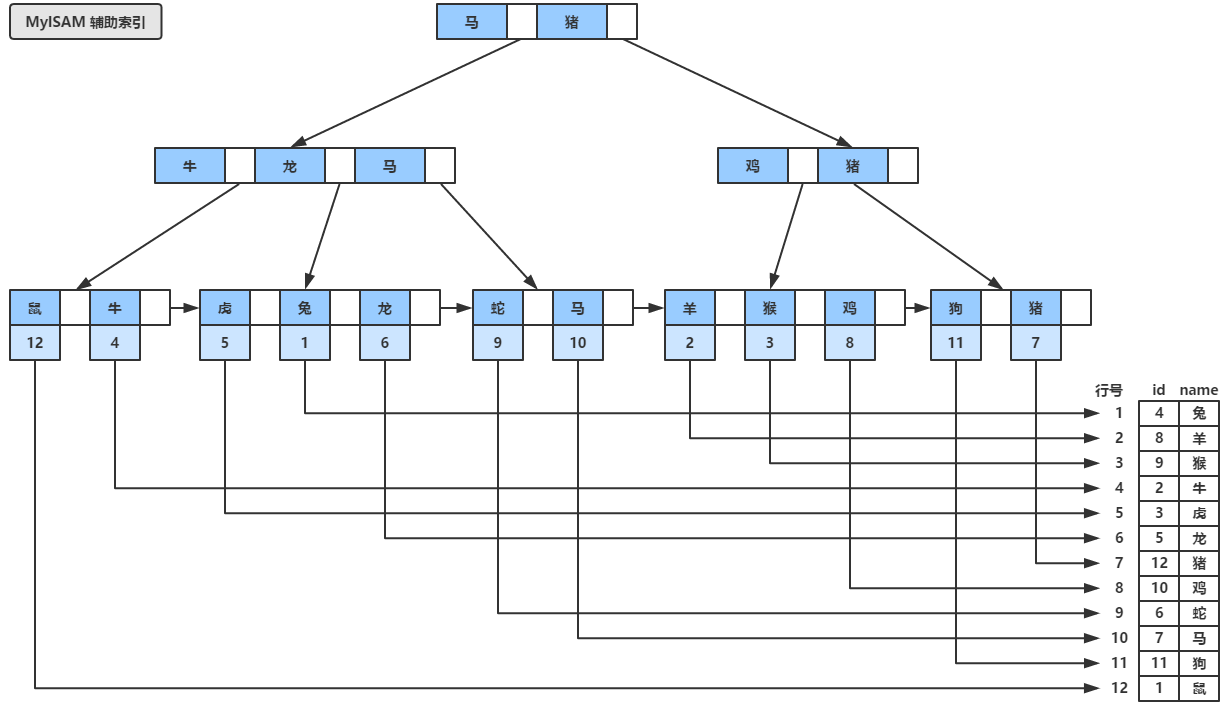
六、简单对比
1、Innodb辅助索引的叶子节点存储的不是地址,而是主键值,这样的策略减少了当出现行移动或者数据页分裂时辅助索引的维护工作,虽然使用主键值当作指针会让辅助索引占用更多空间,但好处是,Innodb在移动行时无需更新辅助索引中的主键值,而MyISAM需要调整其叶子节点中的地址。
2、innodb引擎下,数据记录是保存在B+树的叶子节点(大小相当于磁盘上的页)上,当插入新的数据时,如果主键的值是有序的,它会把每一条记录都存储在上一条记录的后面,但是如果主键使用的是无序的数值,例如UUID,这样在插入数据时Innodb无法简单地把新的数据插入到最后,而是需要为这条数据寻找合适的位置,这就额外增加了工作,这就是innodb引擎写入性能要略差于MyISAM的原因之一。
Innodb和MyISAM索引的抽象图
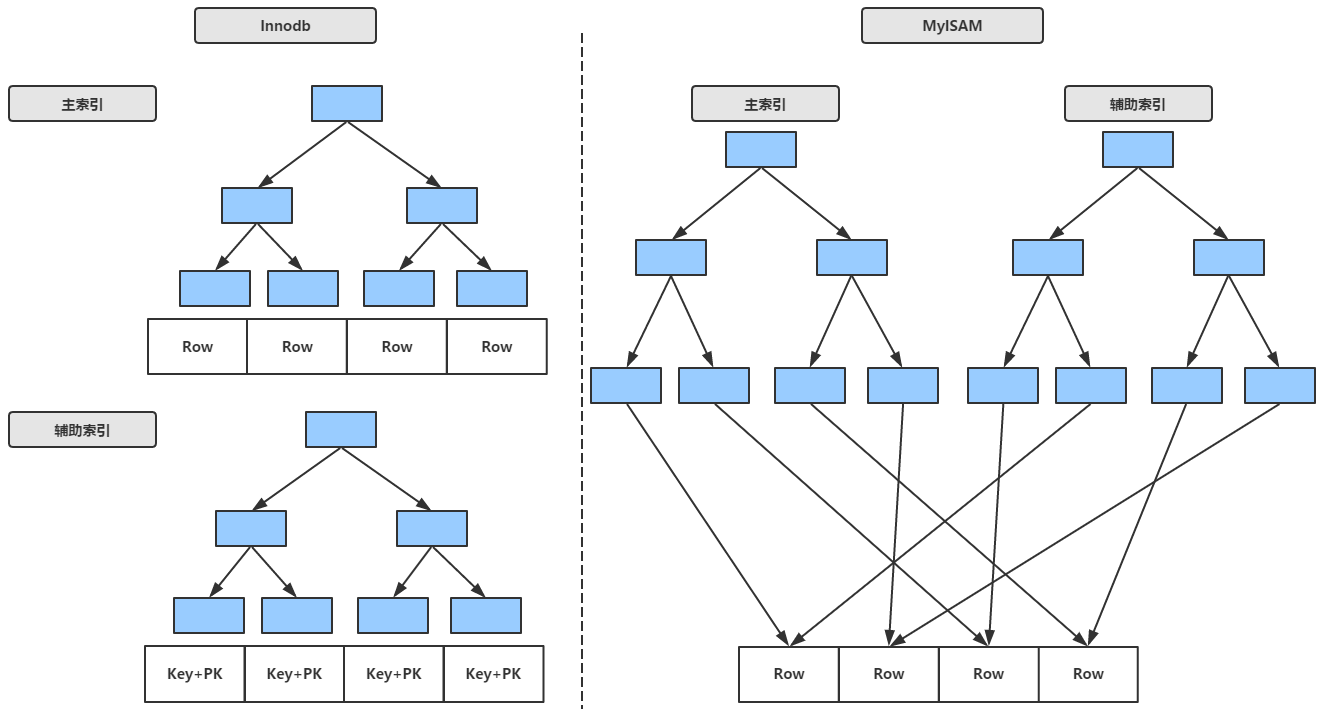
啊 B树的更多相关文章
- B树——算法导论(25)
B树 1. 简介 在之前我们学习了红黑树,今天再学习一种树--B树.它与红黑树有许多类似的地方,比如都是平衡搜索树,但它们在功能和结构上却有较大的差别. 从功能上看,B树是为磁盘或其他存储设备设计的, ...
- ASP.NET Aries 入门开发教程8:树型列表及自定义右键菜单
前言: 前面几篇重点都在讲普通列表的相关操作. 本篇主要讲树型列表的操作. 框架在设计时,已经把树型列表和普通列表全面统一了操作,用法几乎是一致的. 下面介绍一些差距化的内容: 1:树型列表绑定: v ...
- 再讲IQueryable<T>,揭开表达式树的神秘面纱
接上篇<先说IEnumerable,我们每天用的foreach你真的懂它吗?> 最近园子里定制自己的orm那是一个风生水起,感觉不整个自己的orm都不好意思继续混博客园了(开个玩笑).那么 ...
- HDU1671——前缀树的一点感触
题目http://acm.hdu.edu.cn/showproblem.php?pid=1671 题目本身不难,一棵前缀树OK,但是前两次提交都没有成功. 第一次Memory Limit Exceed ...
- 算法与数据结构(十一) 平衡二叉树(AVL树)
今天的博客是在上一篇博客的基础上进行的延伸.上一篇博客我们主要聊了二叉排序树,详情请戳<二叉排序树的查找.插入与删除>.本篇博客我们就在二叉排序树的基础上来聊聊平衡二叉树,也叫AVL树,A ...
- [C#] C# 知识回顾 - 表达式树 Expression Trees
C# 知识回顾 - 表达式树 Expression Trees 目录 简介 Lambda 表达式创建表达式树 API 创建表达式树 解析表达式树 表达式树的永久性 编译表达式树 执行表达式树 修改表达 ...
- bzoj3207--Hash+主席树
题目大意: 给定一个n个数的序列和m个询问(n,m<=100000)和k,每个询问包含k+2个数字:l,r,b[1],b[2]...b[k],要求输出b[1]~b[k]在[l,r]中是否出现. ...
- bzoj1901--树状数组套主席树
树状数组套主席树模板题... 题目大意: 给定一个含有n个数的序列a[1],a[2],a[3]--a[n],程序必须回答这样的询问:对于给定的i,j,k,在a[i],a[i+1],a[i+2]--a[ ...
- bzoj3932--可持久化线段树
题目大意: 最近实验室正在为其管理的超级计算机编制一套任务管理系统,而你被安排完成其中的查询部分.超级计算机中的 任务用三元组(Si,Ei,Pi)描述,(Si,Ei,Pi)表示任务从第Si秒开始,在第 ...
- jquery-treegrid树状表格的使用(.Net平台)
上一篇介绍了DataTable,这一篇在DT的基础之上再使用jquery的一款插件:treegrid,官网地址:http://maxazan.github.io/jquery-treegrid/ 一. ...
随机推荐
- 洛谷 P1903 [国家集训队]数颜色 / 维护队列
墨墨购买了一套N支彩色画笔(其中有些颜色可能相同),摆成一排,你需要回答墨墨的提问.墨墨会向你发布如下指令: 1. \(Q\) \(L\) \(R\) 代表询问你从第L支画笔到第R支画笔中共有几种不同 ...
- 清北学堂4.28Day1(重大更新详见贪心例一)
枚举 用题目中给定的检验条件判定哪些是无用的,哪些是有用 的.能使命题成立的即为其解 . 例一 一棵苹果树上有n个苹果,每个苹果长在高度为Ai的地方.小明的身高为x 他想知道他最多能摘到多少苹果 数据 ...
- ICPC China Nanchang National Invitational -- D. Match Stick Game(dp)
题目链接:https://nanti.jisuanke.com/t/38223 题意:有一堆火柴构成了一个加减法式子,你可以把火柴重新组合,要求数字个数和原来一样多,每个数字的位数和对应原数字位数一样 ...
- opencv+codeblocks +anaconda
study from : https://www.jianshu.com/p/c16b7c870356 #include <cstdio> #include <cstdlib> ...
- 互相关(cross-correlation)及其在Python中的实现
互相关(cross-correlation)及其在Python中的实现 在这里我想探讨一下“互相关”中的一些概念.正如卷积有线性卷积(linear convolution)和循环卷积(circular ...
- 微信小程序与webview交互实现支付
实现原理:点击h5网页的支付按钮——(跳转)——>嵌套改h5的小程序的支付页面——(处理支付)——>跳转至支付完成后的页面 注意:(1)网页h5中,引入微信的jssdk <scrip ...
- 关于std::cin阻塞事件循环以及控制台命令输入功能的方案;
如果将std::cin建立在主线程,将阻塞主线程的所有事件循环,因而要保证事件循环不受影响,需要将std::cin放到 子线程中.同时,如果要实现能够强制终止std::cin阻塞, 可以通过强制终止线 ...
- fork子进程
title: fork子进程 data: 2019/3/21 20:24:39 toc: true --- 这里实在学习socket编程前的小知识点,用来创建多个服务端 学习文档 函数可以有两个返回值 ...
- I/O模型系列之四:两种高性能IO设计模式 Reactor 和 Proactor
不同的操作系统实现的io策略可能不一样,即使是同一个操作系统也可能存在多重io策略,常见如linux上的select,poll,epoll,面对这么多不同类型的io接口,这里需要一层抽象api来完成, ...
- java 源码编译
Java语言的“编译期”其实是一段“不确定”的操作过程,因为它可能是指一个前端编译器(叫“编译器的前段”更准确)——把*.java文件转变成*.class文件的过程:也可能是虚拟机的后端运行期编译器( ...
