A*搜索详解(2)——再战觐天宝匣

　　书接上文。在坦克寻径的，tank_way中，A*算法每一步搜索都是选择F值最小的节点，步步为营，使得寻径的结果是最优解。在这个过程中，查找最小F值的算法复杂度是O(n)，这对于小地图没什么问题，但是对于大地图来说，openlist将会保存大量的节点信息，此时如果每次循环仍然使用O(n)复杂度的算法去查找最小F值就是个非常严重的问题了，这将导致游戏运行缓慢。可以针对这一点行改进，在常数时间内查找到最小F值的节点。

　　一个现成的数据结构是优先队列，python的heapq模块已经实现了这个功能，它是基于堆优先队列，可以中O(1)时间内返回堆中的最小值。我们用heapq存储openlist中的节点，构建新的坦克寻径代码：

import heapq

START, END = (), () # 起点和终点的位置
OBSTRUCTION = 1 # 障碍物标记

class Node:
    def __init__(self, x, y, parent):
        self.x = x  # 节点的行号
        self.y = y  # 节点的列号
        self.parent = parent  # 父节点
        self.h = 0
        self.g = 0
        self.f = 0

    def get_G(self):
        ''' 当前节点到起点的代价 '''
        if self.g != 0:
            return self.g
        elif self.parent is None:
            self.g = 0
        # 当前节点在parent的垂直或水平方向
        elif self.parent.x == self.x or self.parent.y == self.y:
            self.g = self.parent.get_G() + 10
        # 当前节点在parent的斜对角
        else:
            self.g = self.parent.get_G() + 14
        return self.g

    def get_H(self):
        '''节点到终点的距离估值 '''
        if self.h == 0:
            self.h = self.manhattan(self.x, self.y, END[0], END[1]) * 10
        return self.h

    def get_F(self):
        ''' 节点的评估值 '''
        if self.f == 0:
            self.f = self.get_G() + self.get_H()
        return self.f

    def manhattan(self, from_x, from_y, to_x, to_y):
        ''' 曼哈顿距离 '''
        return abs(to_x - from_x) + abs(to_y - from_y)

    def __lt__(self, other):
        ''' 用于堆比较，返回堆中f最小的一个 '''
        return self.get_F() < other.get_F()

    def __eq__(self, other):
        ''' 判断Node是否相等 '''
        return self.x == other.x and self.y == other.y

    def __ne__(self, other):
        ''' 判断Node是否不等 '''
        return not self.__eq__(other)

class Tank_way:
    ''' 使用A*搜索找到坦克的最短移动路径 '''
    def __init__(self, map2d):
        self.map2d = map2d # 地图数据
        self.x_edge, self.y_edge = len(map2d), len(map2d[0]) # 地图边界
        # 垂直和水平方向的差向量
        self.v_hv = [(-1, 0), (0, 1), (1, 0), (0, -1)]
        # 斜对角的差向量
        self.v_diagonal = [(-1, 1), (1, 1), (1, -1), (-1, -1)]
        self.openlist = [] # openlist使用基于堆的优先队列
        self.closelist = set()
        self.answer = None

    def is_in_map(self, x, y):
        ''' (x, y)是否中地图内 '''
        return 0 <= x < self.x_edge and 0 <= y < self.y_edge

    def in_closelist(self, x, y):
        ''' (x, y) 方格是否在closeList中 '''
        return (x, y) in self.closelist

    def add_in_openlist(self, node):
        ''' 将node添加到 openlist '''
        heapq.heappush(self.openlist, node)

    def add_in_closelist(self, node):
        ''' 将node添加到 closelist '''
        self.closelist.add((node.x, node.y))

    def pop_min_F(self):
        ''' 弹出openlist中F值最小的节点 '''
        return heapq.heappop(self.openlist)

    def append_Q(self, P):
        ''' 找到P周围可以探索的节点,将其加入openlist，并返回这些节点 '''
        Q = {}
        # 将水平或垂直方向的相应方格加入到Q
        for dir in self.v_hv:
            x, y = P.x + dir[0], P.y + dir[1]
            # 如果(x,y)不是障碍物并且不在closelist中，将(x,y)加入到Q
            if self.is_in_map(x, y) \
                    and self.map2d[x][y] != OBSTRUCTION \
                    and not self.in_closelist(x, y):
                node = Node(x, y, P)
                Q[(x, y)] = node
                heapq.heappush(self.openlist, node) # 将node同时放入openlist中
        # 将斜对角的相应方格加入到Q
        for dir in self.v_diagonal:
            x, y = P.x + dir[0], P.y + dir[1]
            # 如果(x,y)不是障碍物，且(x,y)能够与P联通，且(x,y)不在closelist中，将(x,y)加入到Q
            if self.is_in_map(x, y) \
                    and self.map2d[x][y] != OBSTRUCTION \
                    and self.map2d[x][P.y] != OBSTRUCTION \
                    and self.map2d[P.x][y] != OBSTRUCTION \
                    and not self.in_closelist(x, y):
                node = Node(x, y, P)
                Q[(x, y)] = node
                heapq.heappush(self.openlist, node)  # 将node同时放入openlist中
        return Q

    def a_search(self):
        while self.openlist:
            # 找到openlist中F值最小的节点作为探索节点
            P = self.pop_min_F()
            # 如果P在closelist中，执行下一次循环
            if self.in_closelist(P.x, P.y):
                continue
            # P加入closelist
            self.add_in_closelist(P)
            # P周围待探索的节点
            Q = self.append_Q(P)
            # Q中没有任何节点，表示该路径一定不是最短路径，重新从openlist中选择
            if not Q:
                continue
            # 找到了终点， 退出循环
            if Q.get(END) is not None:
                self.answer = Node(END[0], END[1], P)
                break

    def start(self):
        node_start = Node(START[0], START[1], None)
        self.add_in_openlist(node_start)
        self.a_search()

    def paint(self):
        ''' 打印最短路线 '''
        node = self.answer
        while node is not None:
            print((node.x, node.y),
                  'G={0}, H={1}, F={2}'.format(node.g, node.h, node.get_F()))
            node = node.parent

if __name__ == '__main__':
    map2d = [[0] * 8 for i in range(8)]
    map2d[5][4] = 1
    map2d[5][5] = 1
    map2d[4][5] = 1
    map2d[3][5] = 1
    map2d[2][5] = 1
    START, END = (3, 2), (5, 7)
    a_way = Tank_way(map2d)
    a_way.start()
    a_way.paint()

　　Tank_way_2省略的代码和Tank_way一致。为了让openlist能够返回F值最小值的节点，需要在Node中添加三个额外的方法。对于pop_min_F()而言，不再需要遍历所有节点，仅仅是从堆顶弹出而已，这将大大缩短程序运行的时间。在Tank_way_2中，用append_Q代替了原来来的get_Q()，这是因为不再需要用Q中的节点和openlist中的节点相比较，仅仅是将Q中的节点添加到openlist中。这样做虽然会使得openlist中存在一些重复节点，不过没关系，对于有相同标记的节点，F值小的那个总是最先弹出，一旦弹出就会加入到closelist中，这意味着当该标记的节点再次弹出时，将不会被使用，也就是说，如果同一个标记的节点被计算了多次F值，总是能够确保使用F值最小的那个，并丢弃其它的。

再战觐天宝匣

　　基于盲目策略的广度优先收索无法有效完成4阶以上的拼图（可参考搜索的策略（3）——觐天宝匣上的拼图），在理解了A*搜索后，可以用这种启发性策略再次挑战觐天宝匣的拼图。

设计评估函数

　　如果将拼图的每一次移动看作“一步”，只要能定义出离评估函数和代价函数，就可以像坦克寻径一样使用A*搜索寻找拼图的复原步骤。

　　我们将g(n)定义为从起点移动到某个状态的步数；h(n)是当前状态到复原状态的距离估值，它用所有碎片的曼哈顿距离之和表示。以3×3的拼图为例，假设拼图的某个状态和复原状态是：

　　左图中，3号碎片的位置是(2,0)，它在复原状态的位置是(1,0)，则3号碎片的曼哈顿距离是|2-1|+|0-0|=1。同理，5号碎片的曼哈顿距离是|0-1|+|1-2|=2。左图距复原状态的曼哈顿距离是所有碎片的曼哈顿距离之和：

　　其中D_n表示第n个碎片的曼哈顿距离，图眼的编号是8。

复原拼图

　　有了g和h就可以开始复原拼图，复原过程和坦克的寻路类似。从拼图的初始状态开始，第一步可以向三个方向探测，从而产生三种状态：

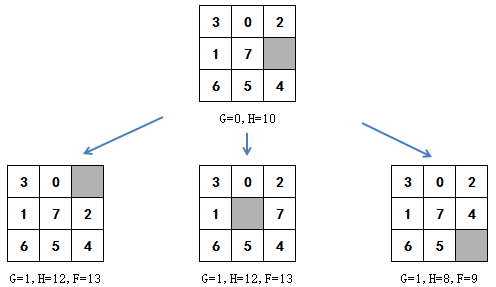
　　此后每一步都选择最小的F值继续探索，如果F值相同，则选择最后加入openlist中的一个：

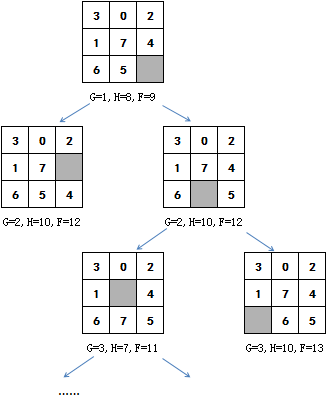
　　最终的复原步骤如图：

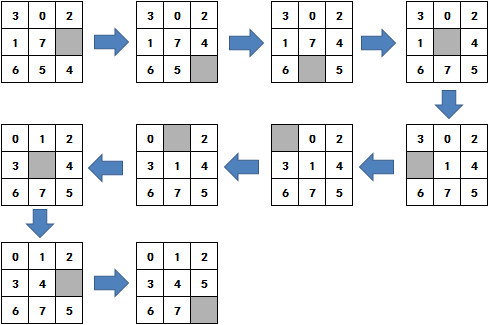
实现A*搜索

　　拼图的实现和坦克寻径类似，完整代码如下：

import random
import copy
import heapq

IMG_END = []  # 拼图的复原状态
EYE_VAL = ' ' # 图眼的值
DIST = {}

def get_hash_value(img):
    ''' 获取img的哈希值 '''
    return hash(str(img))

class Node:
    def __init__(self, img, x=0, y=0, parent=None):
        self.img = img # 当前拼图
        self.x, self.y = x, y # 图眼在img中的位置
        self.parent = parent  # 父节点
        self.hash_value = get_hash_value(img) # Node的哈希值
        self.h = 0
        self.g = 0
        self.f = 0

    def get_G(self):
        ''' 当前节点到起点的代价 '''
        if self.g != 0:
            return self.g
        elif self.parent is None:
            self.g = 0
        else:
            self.g = self.parent.get_G() + 1
        return self.g

    def get_H(self):
        ''' 节点到终点的距离估值 '''
        if self.h == 0:
            self.h = self.manhattan()
        return self.h

    def get_F(self):
        ''' 节点的评估值 '''
        if self.f == 0:
            self.f = self.get_G() + self.get_H()
            # self.f = self.get_H()
        return self.f

    def manhattan(self):
        '' '当前拼图到复原状态的距离 '''
        d = DIST.get(self.hash_value)
        if d is not None:
            return d

        dist = 0
        x_end, y_end = 0, 0  # img_end 中某一个碎片的位置
        n = len(self.img)
        for x, row in enumerate(self.img):
            for y, piece in enumerate(row):
                if piece == IMG_END[x][y]:
                    continue
                # 计算piece碎片在img_end中的位置
                if piece == EYE_VAL:
                    x_end = n - 1
                    y_end = n - 1
                else:
                    x_end = piece // n
                    y_end = piece - n * x_end
                dist += abs(x - x_end) + abs(y - y_end)

        DIST[self.hash_value] = dist
        return dist

    def __lt__(self, other):
        ''' 用于堆比较，返回堆中f最小的一个 '''
        return self.get_F() < other.get_F()

    def __eq__(self, other):
        ''' 判断Node是否相等 '''
        return self.img.hash_value == other.img.hash_value

    def __ne__(self, other):
        ''' 判断Node是否不等 '''
        return not self.__eq__(other)

    def __hash__(self):
        return self.hash_value

class JigsawPuzzle_A:
    ''' 用A*搜索复原拼图 '''
    def __init__(self, level=1, img_start=None):
        self.level = level # 难度系数
        self.n = len(IMG_END)  # 拼图的维度
        self.end_hash_value = get_hash_value(IMG_END) # 复原状态的哈希值
        # “图眼”移动的方向, 上、左、下、右
        self.v_move = [(0, 1), (-1, 0), (0, -1), (1, 0)]
        # 设置拼图的初始状态和图眼的位置
        if img_start is not None:
            self.img_start = img_start
            self.eye_x, self.eye_y = self.search_eye(img_start)
        else:
            self.img_start, self.eye_x, self.eye_y = self.confuse()
        self.openlist = []
        self.closelist = set()
        # 拼图复原步骤
        self.answer = None

    def confuse(self):
        ''' 创建一个n*n的拼图，返回打乱状态和图眼位置 '''
        # 拼图的初始状态
        img_start = copy.deepcopy(IMG_END)
        from_x, from_y = self.search_eye(IMG_END)
        to_x, to_y = from_x, from_y
        # 将图眼随机移动 n * n * level次
        for i in range(self.n * self.n * self.level):
            # 选择一个随机方向
            v_x, v_y = random.choice(self.v_move)
            to_x, to_y = from_x + v_x, from_y + v_y
            if self.enable(to_x, to_y):
                # 向选择的随机方向移动
                self.move(img_start, from_x, from_y, to_x, to_y)
                from_x, from_y = to_x, to_y
            else:
                to_x, to_y = from_x, from_y

        return img_start, to_x, to_y

    def search_eye(self, img):
        ''' 找到img中图眼的位置 '''
        # “图眼”的值是eye_val，打乱顺序后需要寻找到图眼的位置
        for x in range(self.n):
            for y in range(self.n):
                if EYE_VAL == img[x][y]:
                    return  x, y

    def in_closelist(self, node):
        ''' node 是否在closelist中 '''
        return node.hash_value in self.closelist

    def add_in_openlist(self, node):
        ''' node节点加入openlist '''
        heapq.heappush(self.openlist, node)

    def add_in_closelist(self, node):
        ''' node节点加入closelist '''
        self.closelist.add(node.hash_value)

    def pop_min_F(self):
        ''' 找到openlist中F值最小的节点 '''
        return heapq.heappop(self.openlist)

    def enable(self, to_x, to_y):
        ''' 图眼是否能够移动到x,y的位置 '''
        return 0 <= to_x < self.n and 0 <= to_y < self.n

    def move(self, img, from_x, from_y, to_x, to_y):
        ''' 将图眼从from_x, from_y移动到to_x, to_y '''
        img[from_x][from_y], img[to_x][to_y] = img[to_x][to_y], img[from_x][from_y]

    def append_Q(self, P):
        ''' 找到P周围可以探索的节点,将其加入openlist，并返回这些节点 '''
        Q = {}
        for v_x, v_y in self.v_move:
            to_x, to_y = P.x + v_x, P.y + v_y
            # 检验是否可以向to_x, to_y方向移动
            if not self.enable(to_x, to_y):
                continue

            curr_img = copy.deepcopy(P.img)
            self.move(curr_img, P.x, P.y, to_x, to_y)
            # 如果node是不在closelist中，把node添加到Q中
            if not self.in_closelist(Node(curr_img)):
                node = Node(curr_img, x=to_x, y=to_y, parent=P)
                Q[node.hash_value] = node
                self.add_in_openlist(node)
        return Q

    def a_search(self):
        ''' A*搜索拼图的解 '''
        while self.openlist:
            # 找到openlist中F值最小的节点作为探索节点
            P = self.pop_min_F()
            # 如果P在closelist中，执行下一次循环
            if self.in_closelist(P):
                continue
            # P加入closelist
            self.add_in_closelist(P)
            # P周围待探索的节点
            Q = self.append_Q(P)
            # Q中没有任何节点，表示该路径一定不是最短路径，重新从openlist中选择
            if not Q:
                continue
            # 找到了终点， 退出循环
            if Q.get(self.end_hash_value) is not None:
                self.answer = Node(IMG_END, parent=P)
                break

    def start(self):
        if self.img_start == IMG_END:
            print('start = end')
            return
        node_start = Node(img=self.img_start, x=self.eye_x, y=self.eye_y)
        self.add_in_openlist(node_start)
        self.a_search()

    def display(self):
        if self.answer is None:
            print('No answer')

        node = self.answer
        while node is not None:
            print(node.img)
            node = node.parent

def create_img_end(n):
    ''' 创建一个n*n的拼图，将右下角的碎片图指定为图眼 '''
    img = []
    for i in range(n):
        img.append(list(range(n * i, n * i + n)))
    img[n - 1][n - 1] = EYE_VAL
    return img

if __name__ == '__main__':
    n = 9
    IMG_END = create_img_end(n)
    # img_start = [[3, 0, 2], [1, 7, EYE_VAL], [6, 5, 4]]
    jigsaw = JigsawPuzzle_A(level=5)
    print('start=', jigsaw.img_start, ',eye =', (jigsaw.eye_y, jigsaw.eye_x))
    jigsaw.start()
    jigsaw.display()

　　JigsawPuzzle_A中额外设置了难度系数，level的值越大，复原拼图越困难。对于一个拼图来说，level=5已经足以打乱顺序：

　　九九拼图的复原已经非人力所能解决。JigsawPuzzle_A可以快速复原任意难度的4×4拼图，对于更高阶的拼图，即使是A*搜索，面对的搜索数量依然十分庞大，需要耗费相当长的时间，只有level=1的时候 9×9拼图才能快速得到结果。

　　

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！

　　扫描二维码关注公众号“我是8位的”