【页面置换算法】LRC算法和FIFS算法

1. 算法介绍
   1. 1. FIFO：该算法总是淘汰最先进入内存的页面，即选择在内存中驻留时间最久的页面予以淘汰。该算法实现简单，只需把一个进程已调入内存的页面，按先后次序链接成一个队列，并设置一个指针，称为替换指针，使它总是指向最老的页面。但该算法与进程实际运行的规律不相适应，因为在进程中，有些页面经常被访问，比如，含有全局变量、常用函数、例程等的页面，FIFO 算法并不能保证这些页面不被淘汰。
      2. LRU（least recently used)是将近期最不会访问的数据给淘汰掉，LRU是认为最近被使用过的数据，那么将来被访问的概率也多，最近没有被访问，那么将来被访问的概率也比较低。LRU算法简单，存储空间没有被浪费，所以还是用的比较广泛的。
2. 实现思路
   1. 数组作为内存块，另一个数组存储页号
   2. FIFS：

      读入的页号首先在内存块中查找，没有查找到，当前物理块若为空，则调入页号，若非空，则按照先到先出的顺序，调入调出，若查找到页号，则继续查找下一个。

   3. LUR：

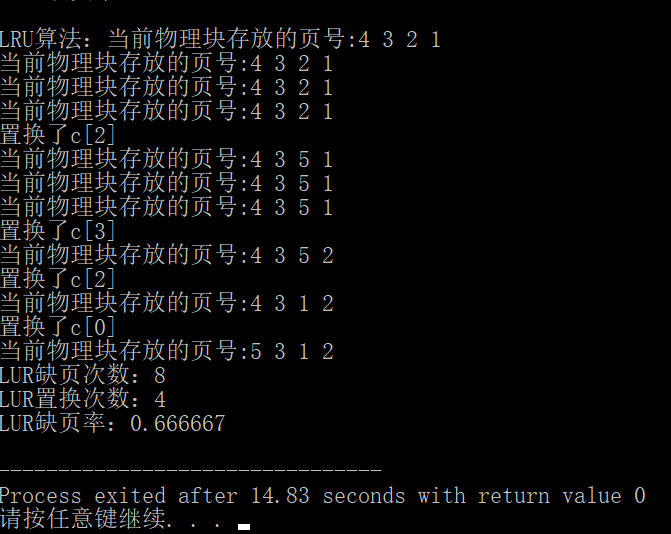
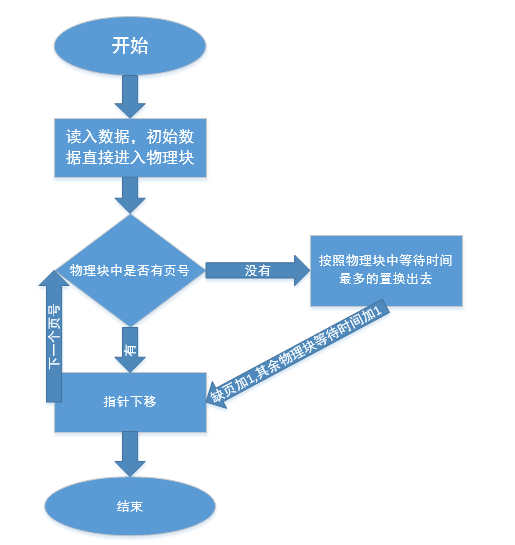
      内存块为空时，先读入的页号进入内存块直到内存块满，将其等待时间都置为0，接下来的页号，如果在内存块中找到，则将该页号的等待时间置为0，若找不到，则查找内存块中等待时间最长的页号置换出去，新进来的页号等待时间置为0。然后将内存块中其余页号的等待时间都加1。

   4. 流程图：

   5. lur:

      FIFS:

3. 代码

4.  #include<iostream>
    using namespace std;
    //伪代码： 内存大小，作业号，
    //物理块，
    int a[],len,b[],i,j,n;
    int c[][];
   
    void readn(int n){
   
        cout<<"请输入页面号(-1结束)";
         len=;
         int m=;
        while(m!=-){
            cin>>a[len];
            m=a[len];
             len++;
            }
            len=len-;
            cout<<"输入完毕"<<endl;
    //        for( j=0;j<len;j++){
    //            cout<<a[j];
    //        }
    } 
   
    void FIFO(int n,int a[]){
        int cnum=;
        for( j=;j<n;j++){
                b[j]=a[j];
   
            }
        //输出第一个b[n],
        cout<<"当前物理块存放的页号:";
        for( j=;j<n;j++){
                cout<<b[j]<<" ";
            }
            cout<<endl;
        int x=,flag=,sum=;
        for( i=n-;i<len;i++){
   
            for( j=;j<n;j++){
                if(a[i]==b[j])
                break;
            }
            int q=x;
            if(j>=n){
                b[x]=a[i];
                x=(x+)%n;
   
                flag=;
                sum++;
            }
            if(flag==){
                    cout<<"置换了b["<<q<<"]"<<endl;
                }
            cout<<"当前物理块存放的页号:";
            for( j=;j<n;j++){
                cout<<b[j]<<" ";
            }
            cout<<endl;
            flag=;
        }
        //计算缺页率
        cout<<"FIFO缺页次数："<<sum+n<<endl;
        cout<<"FIFO置换次数："<<sum <<endl;
        cout<<"FIFO缺页率："<<(double)(sum+n)/len<<endl;
   
    }
   
    void LRU(int n,int a[]){
   
        int cnum=;
        for( j=;j<n;j++){
                c[j][]=a[j];
                c[j][]=;
            }
        //输出第一个b[n],
        cout<<"当前物理块存放的页号:";
        for( j=;j<n;j++){
                cout<<c[j][]<<" ";
            }
            cout<<endl;
        int x=,flag=,sum=;
        for( i=n-;i<len;i++){
            //查找在不在内存里面
            for( j=;j<n;j++){
                if(a[i]==c[j][]){
                    c[j][]=;//将时间恢复为0 
   
                    //等待的时间加1
                for(int k=;k<n;k++){
                    if(c[k][]!=a[i]){
                        c[k][]++;
                    }
                }
                    break;
                }
   
            }
            int q;
            if(j>=n){//不在内存里面，找最久没用的
                int tmp=c[x][],zhen=x;
                for(int l=;l<n;l++){
                    if(c[l][]>tmp){
                        tmp=c[l][];
                        zhen=l;
                    }
                }
                x=zhen;
                q=x;
                c[x][]=a[i];
                c[x][]=;
                for(int k=;k<n;k++){
                    if(c[k][]!=a[i]){
                        c[k][]++;
                    }
                }
                x=(x+)%n;
                flag=;
                sum++;
            }
            if(flag==){
                    cout<<"置换了c["<<q<<"]"<<endl;
                }
            cout<<"当前物理块存放的页号:";
            for( j=;j<n;j++){
                cout<<c[j][]<<" ";
            }
            cout<<endl;
            flag=;
        }
        //计算缺页率
        cout<<"LUR缺页次数："<<sum+n<<endl;
        cout<<"LUR置换次数："<<sum <<endl;
        cout<<"LUR缺页率："<<(double)(sum+n)/len<<endl;
   
    }
   
    int main(){
        //物理块
        cout<<"请输入物理块大小";
        cin>>n;
        readn(n);
        cout<<"FIFO算法：";
        FIFO(n,a);
        cout<<endl;
        cout<<"LRU算法：";
        LRU(n,a);
   
        return ;
    } 

5. 运行结果
   1. 

   2.