最多的划分来使数组有序 Max Chunks To Make Sorted

2018-12-01 11:05:46

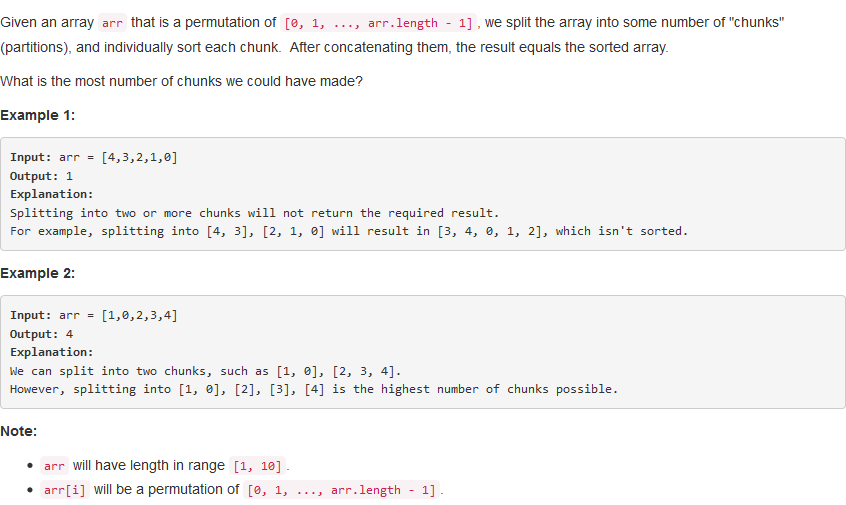
一、Max Chunks To Make Sorted

问题描述：

问题求解：

由于没有重复，所以直观的来看对于每个遇到数，其能够被划分出来的前提是其前面已经有相应的数字，具体可以看下面的图片。

aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD//gAUU29mdHdhcmU6IFNuaXBhc3Rl/9sAQwADAgIDAgIDAwMDBAMDBAUIBQUEBAUKBwcGCAwKDAwLCgsLDQ4SEA0OEQ4LCxAWEBETFBUVFQwPFxgWFBgSFBUU/9sAQwEDBAQFBAUJBQUJFA0LDRQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQU/8AAEQgBKQKSAwEiAAIRAQMRAf/EAB8AAAEFAQEBAQEBAAAAAAAAAAABAgMEBQYHCAkKC//EALUQAAIBAwMCBAMFBQQEAAABfQECAwAEEQUSITFBBhNRYQcicRQygZGhCCNCscEVUtHwJDNicoIJChYXGBkaJSYnKCkqNDU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6g4SFhoeIiYqSk5SVlpeYmZqio6Slpqeoqaqys7S1tre4ubrCw8TFxsfIycrS09TV1tfY2drh4uPk5ebn6Onq8fLz9PX29/j5+v/EAB8BAAMBAQEBAQEBAQEAAAAAAAABAgMEBQYHCAkKC//EALURAAIBAgQEAwQHBQQEAAECdwABAgMRBAUhMQYSQVEHYXETIjKBCBRCkaGxwQkjM1LwFWJy0QoWJDThJfEXGBkaJicoKSo1Njc4OTpDREVGR0hJSlNUVVZXWFlaY2RlZmdoaWpzdHV2d3h5eoKDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uLj5OXm5+jp6vLz9PX29/j5+v/aAAwDAQACEQMRAD8A+4fgN8HPAOq/A/4e3t74G8N3d5ceHtPlmuJ9It3kldreMszMUySSSSTySa7v/hRvw3/6J94W/wDBLbf/ABFVP2dv+SA/DX/sW9O/9Jo6wPB/xF8YeL/j/wCP/DCSaJa+EvCUljE6NZzPf3TXFoJsiXzgiBXIGPLOR6HmgDqv+FG/Df8A6J94W/8ABLbf/EUf8KN+G/8A0T7wt/4Jbb/4iuM8a/tL2fhj47+EvhrYaLLrMmqXS2eqarHcBItKmkt5ri3iYbT5kkkdtK20EbV2E/fXPtVAHEf8KN+G/wD0T7wt/wCCW2/+Io/4Ub8N/wDon3hb/wAEtt/8RXb1418U/jV4s+FPiC1udQ8D2l54En1Sx0r+17XWgb/fdSRwrILMwgMqyyAECXdgFgO1AHXf8KN+G/8A0T7wt/4Jbb/4ij/hRvw3/wCifeFv/BLbf/EV29FAHEf8KN+G/wD0T7wt/wCCW2/+Io/4Ub8N/wDon3hb/wAEtt/8RXG/HP45eK/g1b6tryfDz+2PAuh20d3qmsnWYoJ/LLfvDbW2xjIY15Ido89FzXs0Ey3EMcqZKOoZcjHB5oA4v/hRvw3/AOifeFv/AAS23/xFH/Cjfhv/ANE+8Lf+CW2/+Irt68h+M/x5vvhP4m8KaZB4I1PW7DWNW07TLrXPPit7Ky+13It05Yl5ZAx3FFXAGCWGRkA6f/hRvw3/AOifeFv/AAS23/xFH/Cjfhv/ANE+8Lf+CW2/+Irt6KAOI/4Ub8N/+ifeFv8AwS23/wARR/wo34b/APRPvC3/AIJbb/4iud+Knxo1jwn4utfCfhLwxbeKPEB0uXXL3+0NVXTbOxskfYHkmMb/ADO+5VULj5HLMoXNc3qf7QOq+Of2XG+MHw5k0u0it9JvNXnstftHut32aOXzLcGGaMBhJEV8wFlIGQDkUAejf8KN+G//AET7wt/4Jbb/AOIo/wCFG/Df/on3hb/wS23/AMRXSeGNUk1vw1pOozKqS3lpFcOqfdBdAxA9ua06AOI/4Ub8N/8Aon3hb/wS23/xFH/Cjfhv/wBE+8Lf+CW2/wDiK7eigDiP+FG/Df8A6J94W/8ABLbf/EUf8KN+G/8A0T7wt/4Jbb/4iu3ooA4j/hRvw3/6J94W/wDBLbf/ABFH/Cjfhv8A9E+8Lf8Agltv/iK7eigDiP8AhRvw3/6J94W/8Ett/wDEUf8ACjfhv/0T7wt/4Jbb/wCIrt6KAOI/4Ub8N/8Aon3hb/wS23/xFH/Cjfhv/wBE+8Lf+CW2/wDiK7eigDiP+FG/Df8A6J94W/8ABLbf/EUf8KN+G/8A0T7wt/4Jbb/4iu3ooA4j/hRvw3/6J94W/wDBLbf/ABFH/Cjfhv8A9E+8Lf8Agltv/iK7eigDiP8AhRvw3/6J94W/8Ett/wDEUf8ACjfhv/0T7wt/4Jbb/wCIrt6KAOI/4Ub8N/8Aon3hb/wS23/xFY/wR0XT/D178RdO0qwttM0+38TuIbSzhWGKMGxsyQqKABkkngdSa9Prz34U/wDIf+Jn/Y0N/wCkFlQB6FXjPg34a+EPF3jX4n3uu+FdE1q9XxIsQudR06G4kCDTbEhdzqTgEnj3NezV558K/wDkZvij/wBjQP8A02WFAFv/AIUX8Nv+ifeFf/BLbf8AxFH/AAov4bf9E+8K/wDgltv/AIiua+KnxA8YaX8WvAPgnwnLolmfEFnqd7c3ms2c11sW1+zYVFjmiwW888knGBxUfxo+Pt98JPE/hHS4vBOp63Y61q+naVc64J4reysjd3IgTBYl5ZAfmKKuAMEsMjIB1P8Awov4bf8ARPvCv/gltv8A4ij/AIUX8Nv+ifeFf/BLbf8AxFdxRQBw/wDwov4bf9E+8K/+CW2/+Io/4UX8Nv8Aon3hX/wS23/xFc98VPjRrHhPxdbeE/CXhi28T6//AGXLrl8dR1ZdMs7GyR9ivJMY5Pmdwyqu3HyOWZQM10XwU+LWk/HP4X6B430RJIbDVoS/kTFWeGRXZJIyVJBKujLkEg4yODQAn/Ci/ht/0T7wr/4Jbb/4ij/hRfw2/wCifeFf/BLbf/EV3FcX8SvEvjLw/Bp8fgzwbD4tvbl3ExvNVTT7a1RVzl3KSOSx4UKh75KjqAR/8KL+G3/RPvCv/gltv/iKP+FF/Db/AKJ94V/8Ett/8RSfBL4q23xq+GOjeMLXT59JF8JY5bC5ZXe3mileGWPcvDASRuAw6jB4ziu5oA4f/hRfw2/6J94V/wDBLbf/ABFH/Ci/ht/0T7wr/wCCW2/+IrR+IGreKtI0aGXwf4fsPEeqPOEa21LUzp8Mce1iZDIIpSSCFG0Lzu6jFZHwR+KbfGDwN/bk+jvoV9Bf3ml3lg1wtwkdxbTvBL5cygCRNyEq4AyOwNAE3/Ci/ht/0T7wr/4Jbb/4ij/hRfw2/wCifeFf/BLbf/EV3FY3jPxfpPgDwpqviPXbtLHSNMt3urmd/wCFFGeB1JPQAckkAcmgDA/4UX8Nv+ifeFf/AAS23/xFH/Ci/ht/0T7wr/4Jbb/4iuZ+DHxg1/46/DDWdYtdBi8D+JLTUrvSVsNYJvUt5oXC5lWMxk9eVVhg8bjWn+z/APEDXPiN4I1C+8Rpp66tp+u6po0r6XC8UEn2S8ltw6o7uy7hGDgsetAGn/wov4bf9E+8K/8Agltv/iKP+FF/Db/on3hX/wAEtt/8RXcUmaAOI/4UX8Nv+ifeFf8AwS23/wARR/wov4bf9E+8K/8Agltv/iK7iigDh/8AhRfw2/6J94V/8Ett/wDEUf8ACi/ht/0T7wr/AOCW2/8AiK7iigDh/wDhRfw2/wCifeFf/BLbf/EUf8KL+G3/AET7wr/4Jbb/AOIruKKAOH/4UX8Nv+ifeFf/AAS23/xFH/Ci/ht/0T7wr/4Jbb/4iu4ooA4f/hRfw2/6J94V/wDBLbf/ABFH/Ci/ht/0T7wr/wCCW2/+IruKKAOH/wCFF/Db/on3hX/wS23/AMRR/wAKL+G3/RPvCv8A4Jbb/wCIruKKAOH/AOFF/Db/AKJ94V/8Ett/8RR/wov4bf8ARPvCv/gltv8A4iu4ooA4f/hRfw2/6J94V/8ABLbf/EUf8KL+G3/RPvCv/gltv/iK7iigDh/+FF/Db/on3hX/AMEtt/8AEUf8KL+G3/RPvCv/AIJbb/4iu4ooA4f/AIUX8Nv+ifeFf/BLbf8AxFH/AAov4bf9E+8K/wDgltv/AIiu4ooA4f8A4UX8Nv8Aon3hX/wS23/xFH/Ci/ht/wBE+8K/+CW2/wDiK7iigDh/+FF/Db/on3hX/wAEtt/8RR/wov4bf9E+8K/+CW2/+IruKKAOH/4UX8Nv+ifeFf8AwS23/wARR/wov4bf9E+8K/8Agltv/iK7iigD5K8S/CbwPF4j1VE8F+HURbuVVVdJtwAA54+5RXV+Kf8AkZ9X/wCvyb/0M0UAekfs7f8AJAfhr/2Lenf+k0dcJ8GriJP2nv2hIWlRZnutDKIWG4/8S1eg713f7O3/ACQH4a/9i3p3/pNHXQn4d+FD4t/4So+GdHPifG3+2/sEX23GzZjztu/7vy9enHSgD5U1r9lD4t6H4k8Dz6N8SLLWYoPGdx4j1C+ufD0STwSS2t0jXEjG4/f4EiQKgA2qUxgR4r3O6+M98P2k9L+Gmn6bZ6tpsmhT6nqepWt3un0udJEWOOeIAhFkVwUyQWw2BhSa9ZqGK0ggllljhjjlmIaR1UBnIGAWPfjjmgCavlr9ov4Za78V/Glv/wAI38Nr/SvGenXNqulfE2fVbeG30+JJBI8iRpM00nytMnlNEAxYgkKc19S0UAeSeM/jXd+Hvj58Pfh1pmn2etJr0N9Pq0sV1m60qOGJXimeIA4jkY7NzEZJAGa9bqFLOCO5kuEgjW4kADyqgDMB0BPU4qagD5d/aHh+JvjP4lWehn4W6h4u+FGmiG9kttO1ixt/7bvFKui3AmlVlt4mAPlgfvGALHaNrd/8R/jjqfgrxr8J/Ddlodpe6n4u1BbfUtJa+X7dplt5DyNcCNMh442RlZ8hcgAElhj2OofskH2r7T5Mf2nZ5fnbRv25ztz1xknigCavnf8Aayt/HviRPCujeEfh1f8Aiq20/XtI8Qz6jBqVnbRgWt6sz2+2aVWLlYxg42/OOeDX0RRQB4t8WvjzrPw78PfD2a38MQS+KPE+tWOnzeFrvUYxfQwzNtneIR7xK0OQWIOwKGYsAK9pqF7SCS5juGhja4jUqkpUF1B6gHqAcCpqAPl39ov4J6tr3xr0bxvF4Rv/AIjeF5tFXSdV8KWOqQWSTTwXDz2ktwszIk8AaaUNGWwCEYo+MCa8+H978IP2E/Heg6/NZRa3N4e1/ULyO0bFvHcXS3Ny8MROMqhlKA4GQucDNfTlYXi3wH4Z8f2cNp4o8O6T4ktIZPNig1exiuo43wRuVZFIBwSMjsaAGfD7/kQfDX/YMtv/AEUtdBUcEEdrDHDDGsUMahEjRQqqoGAAB0AFSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAV578Kf+Q/8TP8AsaG/9ILKvQq89+FP/If+Jn/Y0N/6QWVAHoVeefCv/kZvij/2NA/9NthXodeefCv/AJGb4of9jQP/AE22FAHHfEq5itf2s/g080qQp/YfiIbpGCjP+getZH7W1l498TjwhpHhH4d3/im20zxBpHiOfUYNSs7aPFrdiV7cLNKrFysYwcbfnHPBr2rxX8PPCvjt7N/EvhnR/ETWZZrZtVsIrowFsbinmKdudq5x1wPSugAwKAPGPi18d9Y+Heg/DuS28NQTeJ/FGtWGnz+F7vUEF7BDMcXDxCPcJWhyCxB2BQzFgBXtFQtaQPcpcNDG1wilUlKgsoPUA9QDgVNQB8u/tE/BPV9e+NekeNo/CV/8RvC82irpWqeE7LVILNJriC4ee0luFmZEngBmlDRlsAhGKPjAil8Qa5+xp+y1o8bWGk6/46udUMw8OwXZiF3cX2oGWa3tAF3SGMXJC4XkJkgDivqeoZbO3nnhmkgjkmhz5UjoCyZ67T2z7UASIxZFJG0kcj0rxP8Aak1D4pHw7pWi/DXw3e6pHqkzR6zqumX9rbXthaADK232h1XzZMlRJz5YBbBO2vbqKAPnbXfiZcfs7/snz6zZeArXwXfaDbfZdI8H6vqsLG5ZWwkSSws/mSyKGZVBLu3Xkk175ol7PqWjWF3dWrWNzcW8cstq5y0LsoLIT3IJI/CrE9pBdGIzQxzGJ/MjMihtjYxuGeh5PPvUtAHnnxygXUvBZ0q4+Ht/8SdOv5liutJsLi2hZVX51djPNECoZV6NnkcYzXmPw7j1j9mP9mfxdqWs2+naBHYS3+paB4a1XV98Gl25XNrpzXRzuJdT93dgy7FJCivpGorm0gvECTwxzorBwsihgGHIPPcUAc98MfFGo+Nvhx4W8Q6vpEmgapqumW19daVKSWtJZIldoiSAcqSRyAeOQK5L4+fCHXPi/p/hy10fxZF4ZTSdUj1WWG50tb+C9eIEwrJGZEyEkxIBnG5EJHyivU6KAPBP2XPhr49+Fdl4/bx3r1pqEWpeJb/UrRIrGO2DLJMWNyWWV8CUEERnBTGMnNWf2RLxLvwF4rZSDnxt4jYFTkEHVLg5Few6/pml63pNzpus2VrqWm3SGOezvYVmimXurIwIYexFYmg6Dofgu0gsfDek2OiaXGWZbDTrVLaFCxyxCIAoySSeOtAHVSSCJCzcADNZ6Lcahly5ii7Ad6sXp86xZk5BAI+lVLe8kMCQwxkuBgsegoAV3m02RN0nmRtxg1pRuJEDL0IzVOLT9zeZcN5j+nYVJZXRud/yBFXAAFAFqiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioLu5+yxhtu7JA+lTA5GaAFooooAKKKKAPnPxUf+Kn1f/r8m/8AQzRR4q/5GfWP+vyb/wBDNFAHpX7O3/JAfhr/ANi3p3/pNHXoVee/s7f8kB+Gv/Yt6d/6TR12d3r2mWGpWWnXWo2ltqF9v+y2k06rLcbRlvLQnLYHJwDigC/RRRQAUUUUAFFcX4k+MXhLwl430nwjqepSxeItURJLWyhsp5yyPJ5SuzRoyxqX43OQPeu0oAKKKKACiiigAooooAKKKKACiiigAooqOeeO1hkmmkWKGNS7yOQFVQMkknoBQNK7siSiua1/4jeHfDnhOTxNdaiLjQ4yqm706J70Eltg2rCrs3zHBwDjnPSrPgnxrovxF8Kab4l8OX6anompReda3aIyiVMkZwwBHIPUCknfVDlFxbjJWaNyiiimSFFFFABRRRQAUUUUAFFULHXtM1O/vrG01G0ur2wZVu7aCdXktywyokUHKEjkZxmr9ABRRRQAV578Kf8AkP8AxM/7Ghv/AEgsq9Crz34U/wDIf+Jn/Y0N/wCkFlQB6FXnnwr/AORm+KH/AGNA/wDTbYV6HXnnwr/5Gb4of9jQP/TbYUAeh0VS1HWtP0h7VL6/trJ7uZbe3W4mWMzSn7qJkjcx7Ac1doAKKKKACiiuV+IvxQ8NfCjSLTU/FGoNp9pd3a2NuY7aW4eWdld1RUiVmJKxueB/CaAOqoqrpepW+s6Zaahasz2t3Ck8TPG0bFGUMpKsAynBHBAI7irVABRSEgDJOBVG+17T9Ltpbm7u4bW2iG6SeZwiIPUseAKG7asqMXJqMVdsv0VXsr+21K1iubSeO5t5VDxywuGV1IyCCOCCOc066uBbQlzyew9aBNNOzJqK5XxX4k03wd4bvPEXiXVotH0e0UPPdTkiOJSwUFsdBkgfjUvh3xPp+u6TZavo2qWmuaJep5ltfWMyzQyr6o6kg/gaBGnGoutSk8z5gnRTVye1jnjKsoHoQORVG5JtLtbhfmR+tLrniTTPDWgX2t6neR2WlWMD3NzdSfdijUZZjjsAKAH6fIY3e1k6jpUbQTWEzPCN8R/hrE8MeL9F+I2mw6/4U1ey17SZf9VfafOs0TkHBG5TjIPBHUY5rrUJKjcMHHIoAoG7uLpdkcJjzwWPardpbC1iCjknkmi8u4bC0nubiQRQQo0kjnoqgZJ/IVz3g74meFfiH4ZfxB4X1+x8QaOm4PdabMJwjKMsrBckMB/CRnpxQB09Fcd8OPi54U+LVtqc/hbUn1BdMuBaXiS2k1tJBKUWQKySorDKOrdOhFdjQAUUUUAFFFFABRRRQAUUVSj1rTptWm0uO/tpNThjWaWyWZTMkZOA7JnIUkEAkYoAu0UUUAFFFFABRRRQAUUySVIV3OwUe9UbnVFCjySCc8gg9KALV9H5tpIvfGaLKTzbWNu+MGpI5FmjDDlWFVNNzG00J/gagC9RRRQAUUUUAfOfir/kZ9Y/6/Jv/QzRR4q/5GfWP+vyb/0M0UAek/s8Hb+z/wDDY4Jx4a044HX/AI9o6+MdR+If9s/tKfCz4ieK/DHjbT/EV14mvbO10u78MX4/s7S00+8jggi/dYkkkdvPlKFsbgD8sQNfZ/7O3/JAfhr/ANi3p3/pNHXY6j4e0vV7/TL6+0+2vLzTJWnsbieJXe1kZGjZ42IypKMykjsxHegDQHIrgL3xn47g+I8ejW/w6+1eE2kRW8T/ANtwJtUoCzfZiN52tlcZ5xmvQKKAPn74jeMta8CfHnQ7Twbqt14t1TXzENY8CTSGSOztFwh1KOY8WQUDBR/knPCqHyx+gaz7Hw/pemanqOo2mnWlrqGosj3t1DCqS3LIoRDIwGX2qABnOAMCtCgDxmL/AJPHuv8AsQof/TjLXSeNvGnjzQvFthp/h74cf8JPocyxm41j+3ILT7OWchx5Lgs+1QG465wOlZ/iL4fa2vxy03xxo/iTSNPifSYtFvtM1LT3nkngW5aYtDIs8exzuKgsrgdcHpXqVAGJrPjbQPDuuaJo2qazZafq2tySRaZZXE6pLePGu91iUnLFV5OK26858Y/Bm28e/FHwj4s1nVZZ7Hwq7Xml6NHbxqiXrI8ZuHmwZGAR8CMFVyAx3EDHo1AHA/Enxj458MX1hF4S+Hn/AAmltMjG4uP7bgsPs7AgAbZAS+Rk5HpXR+IfGuheEG0hNe1ey0aXV7yPTrBLy4WM3N04JSGPJG5ztbAHJxW3XnXxP+DVr8WfEPhG41vU5ToPh3UYtZTRo7ePFzfQtut5XlILqqEk7ExuPUkZBAPRa4f4m+LfGfhaPTz4P8Bf8Jw0xcXK/wBsQ6f9mA27T+9B37st06bfeu4ooA53XPHekeDPDllq/i3ULLwvDcPBbub+6RY47iUhVh8w4DHcdoI69a6KvN/jV8F7X45aZpeha3qcsPhWK8jvNR0mGCMnUTFIksKGVgWjQOgLbMMwONw7+jgYGB0oA5H4leJvFfhjSrWfwl4M/wCE1vJJ/LmtP7UisPJj2k+ZvkBDcgDA55z2qS7+INn4S+H0Xinx29n4Igigik1Bb+9jaGykcqvltMMK3zMFBHBJFdVmvPvjj8Ik+OXgiXwhfaxNpfh6/kVdXgtreOSW9thyYVdwfKyQp3qNwxwQeQAegRyLLGrowdGAZWU5BB6EGvAv2rdfvpLTw94R/sjXrrw3rUzPrt9oenzXUiWkeCbceWDtMxIUk9FD17zaWsVjaw20CCOCFFjjQdFUDAH5CpSoIIPesa1N1YOCdr/1+J6eW4yOX4uGKlT5+XVK7WttHdJ6p6rR6pdj52/Yd1221H4BWlha2d5arp1zdpuuLZoonDTyuvlseHABAOOhBB5FWP2Otd07wv8Asa+BtY1e9g03SrDSJbm6vLmQJFBEkkjO7MeAAAST7V6tqnhuXw34Lk0vwS2ieFpI2zAbuwMtnFufc+YY5IiS2W6OOTnnpXBeFPgFeaF+zRpXwqtfF3lCKxOn3Wt2thE5ngdm81UilLopZXZQTux1waWHpujSjTbvZWLzbG08xzCvjKUHGNSTlZu7V9dXoeuaLrNh4j0iy1XS7yDUNMvoUubW7tpA8U0TqGR0YcFSCCCPWvG/2ntX8Q21z8NNH0HxHfeGV1zxFLZX91pwj857ddNvZzGpdWCktCmGAyMZFereCPBul/DvwbofhfRIDbaPo1lDYWcTMWKxRoEUEnqcAZPc1b1Xw9peuTWM2o6fa30thMbi0e4iVzBIY3jLoSPlYpI65HZ2HQmtzyT4g+Gvxw8UWngjVf8AhMvGXibW7vXNA8I31gdES0hvF1HVGuF+z2xlURRI3lRKWkPADtkM1afgv4oeMJ/Bn7QOla1441LwY/gaexu9M1bXLu01K5sGa3EzW9xJbgpOjyJt2cyYlKg7sV9V3nwc8Caho11pFz4O0K40u6s7bT57OTT4mikt7fP2eIqVwUj3NsHRcnGKh034IfDzR9PNhYeB/D1lYma3uTbQaZCkbSwHMEhULgtGeVJ5B5HNAHnf7J3xG8RfFzTPFPijxXdy6XrrX62M3ghht/4RwRoNsb5UO0kwbzi54KugX7pJ9P8Ail4g1Xwt4F1LU9FQyalAE8pRpVxqecuoP+j27LI/BP3Tx1PANbFp4W0aw8QX+u22lWdvrWoRRw3moRQKs9wkefLWRwMsF3HGc4ycVqUAeOfAv4k+L/HOp6rB4lgaGG3hR4SfCGpaJlixB+e7kYScdlwR1NdN8dPHWs/Dj4Wa7rvh3QL3xNr0MaxWOnWNrJcu00jhFdo41ZzGhbe+0E7UbHNd7RQB8R/sU3ejeGP2hfi14fsbXxRcXl/Y6Nd3eqa5oV3aS3V35Vy9zcXJljXymlkkLIGxkcJkLx9uVnWfhzStP1nUdXtdOtbfVdRWJLy9ihVZrkRgiMSOBlgoZgM9MnFaNABRRRQAV578Kf8AkP8AxM/7Ghv/AEgsq9Crz34U/wDIf+Jn/Y0N/wCkFlQB6FXnnwr/AORm+KH/AGNA/wDTbYV6HXnnwr/5Gb4of9jQP/TbYUAeRftbeB/CsPjT4UeMZrG1bxUPHOg2Qv55C0kNsJ3YrGGOIwSfmKgbsDcTgY+nkdZUV0YOjDIZTkEetcN43+BHw4+Jerpqvi3wJ4d8S6mkSwLeatpkNzKsYJIQM6k4BZjj3PrXYaTpNloOlWemabaQ2GnWcKW9ta20YSKGNAFVEUcKoAAAHQCgDkPib4u8a+Fm08eEPAH/AAm4mD/aT/bMGn/Zsbdv+sB37st06bfeuK/aS8SXfg7w3oPijTvE114d8YW0vk6X4eRWvYdenkC5sHtU+aUtt4lTDRYL5C7wfb6oXOgaZeaxZatcadaz6pZRyRWt7JCrTQJJt8xUcjKhti5APO0Z6UAQeEtR1PWPDGlX2taT/YWr3FtHLd6Z56z/AGWUqC0fmLw+05G4cHFeYftEf8jD8Ff+x8t//Tff17LXm3xu8Aaj45svCdzpGvad4e1Pw7rsWs29xqtm11byssE8PlsiyxHkTk5Dj7tAGz8SvE3izwxpdpP4S8Gf8JteSTbJrT+1YrDyY9pO/fICG5AGBzzmpbv4gWfhP4fw+KfHb2fgmCOCKTUFv72NobKRyq+W0wwrfOwXcOCSKmk8Sz6TBZQXwhvrw28bT3Fopjikcj5mRSWKqSCQCzYBHJ61518cfDNv8cvBMnhC/vbnS/D1/Iq6vBbRRSS3tsOTCrup8rLBTvUbhjgg8jJ1YJ2bM3Uina56qZv7WlCxODbY3B1OQw9fevJf2rvBfhTWvg54guNfERudO0y9udNjnujGrXIt22nZuAkYHBAIODyBXdaR4kt9HtUt4bQiGNVRFD/dVRgDp6Vm+L7bwr8QLe2g8S+FrDXobZzJDHqMKTrGxGCVDKcHHFc9eUKtKVNNarrsenleYU8BjqOKcpJQkn7uktGnZX01tZ+TZnfB/wAT+H/DX7P/AIa1/UNasrTSdL8P2j315LcKIrUJbIX8xs4XHcGvQZb+21rRrPUbC4ivLG5jSeC5gcPHLGy5V1YcEEEEEdjXm+q/CPRPF/wv13wR4XitvAGj6szRaiNI0+BjNDImyZQrqUV3QBd5ViMDjgV6B4S0PTfC3h3TPDGlWxtdJ0mzisLWEsW2QxII0XJ5OFUcmuilpTin2M8XVp4jEVK1G/LKTava+rb1tp16FX4heI73w18NfEmuaVBaXepafpdxdWtvfzrBbyzJEzIkkjFVRSwALEgAHORXEfBj4eD4QfDXX7vW9V09n1XUbzxRfSWUX2fT7EzASOkKl22xKFLFi3JLtxurvdd8P2er6Pf6PrGnW+s6LfxNBdWV5EJYZ42GGV1IIII4IIrO8X+F9R8T+Crnw7od+PCaSwrapdw2cc4gh4DKkTjZ9wFRkEDI4OMVqchr+D/EGleNPCun6xpF/bavo99EJrW8tJBJFNGejKw4Ip2t2g0/SL+7hKl4IJJUSZwiEqpIDMcADI5JPFUvhf8ADjRfhD8PtB8GeHYZIdF0W1W0tllfe5UdWY92YksTxyTwK6G/srbUrG4tLyCK5tJ42imgmUMkiMMMrA8EEEgg0AeNfsx/D+/8MaDr/jTW7vTl1Xx3PbeILzTtGAXT9PY2kUZSJhI4kPyZeYNhzyBjFepeDvGmg/ELw7a694Z1ez13Rbrd5F/YTCWGTaxVsMODhlIPuDUF14T/ALO8D/8ACO+EprbwklvaLZ6dJa2UckNiigKgSE4QhQMBelZXwa+E2jfBD4daX4P0JppbGyMsjT3O3zJ5ZZGllkYKAoLO7HCgAZwAAKAO1Y4Un2714L+zF4O1m71HxR8VPEM2k2ur+N47QS6PoO17S1W182NWMyyOJ5XD/M4IGFVcfLXvTKrqVYBlIwQehFY+geFtK8F+GYdF8M6dYaDptrGwtLS0t1jtoCSWyI02jG4kkDGcnnmgDyj4E/8AJav2hP8AsZrD/wBM9lXq3hbxroPji2vbjw/rFlrMFjeS6fdSWM6yrDcxHEkTEHh1OMg+o9a4D4Q/DLXPCV58QtZ1TxRpmsa74s1CO+e40nTmt7e0eOzhtkAjeaUtxCrHL8knpW18Gfg/YfBvQNVs7a9m1XU9a1S41vV9Tnijha8vZtvmSeXGAiDCKAqjgKMkkkkAzP2pPFOr+CP2dfiJr+gXzabrWnaLcXNneIoYwyquVYAgg4PrXzt4Y+I/jLwH8YrePxD8RNY1rwxZ6/rGjXUF5DCQbW30OPUWnbZGC0gldtuMBUUKAec/ZuuaFp3ifR7zSdXsbfU9MvIzDc2d3EJIpkPVXU5BB9DWb/wr7wwdRF+fD2mG+FzJeC4NonmCeSEQSS7sZ3tEojLdSoAPFAHyd8IPil4ov/jx4L0Q6n4vTwn4z8Nahqar4r1XTbm5kRBA1vdQpa/NbHbK2Vb5TkYXKnGr+zR8XfFHxG+LH/CMa54zN9o3hi0u/wCyNShhEX/Cbxi5eA3pJQKVttgjYRHDSP5mdhTPv3h74BfDTwk0jaJ4B8N6Q8iTRO9jpcMLMkqhZVJVQdrAAEdCBit2H4e+F7Y+HjD4d0uE+HkMejmO0jX+zkKeWVgwP3YKfKQuARxQBuzu0cEjL95VJHyluceg5P0r56+Gvxm+IPiXx3pemaxavHpk8jLMx+HutadgBGI/0ieUxR8gcsMHp1Ir6JooAK+X/ht4J8JfDn9tTxHZeGbS006O+8D293dMkxklubp9Tud7ySMxZ36D5iSAFAwABX1BXnVh+zl8K9L8Tx+JLP4c+F7XxBHcm8TVIdIgW5WfcW8wSBdwbcSc5zk0Aei0UU2RiqMVG4gcD1oAdRVayu/tSNkbXU8ipZ5lgiZ26CgCSis1I7m+G9pTEh6BaaZZ9OdRIxkiPegBzr9r1Io/3EHSrklpFKm0oAOxA6VRuibe6S5T5kbrWjHMkqBlYEGgChYObWd7dzwTlakOYdUB7SL/AJ/lVS9bzrh5IjkRgZIq6iC/SCbJUqecetAFyiiigAooooA+c/FX/Iz6x/1+Tf8AoZoo8Vf8jPrH/X5N/wChmigD0r9nb/kgPw1/7FvTv/SaOvF/iYs3gH9orwNf6evjfQLLU/Eawat4h1LWZ7rQb2OeF1isY7UzyCNnneJEYxRKhQgMcgN7R+zt/wAkB+Gv/Yt6d/6TR1TuPgJpureLbTXNe8SeJfEsVjqP9q2Gj6nfIbC0uAxaN1ijjQv5ZOUEjPtIBHIBoA9OrhL340+HLD4hxeCpYdcOtyOkavHoN69nll3DN0sRhAweSXwDweeK7uigDxv4gfFnXPg/8SNJXxFHaap4E8T3kOmabJp0ZGpadesoAjeHJa5icgtviG6PncpT5l9krkbb4WaBD8RrvxzNBNf+JJbdbSC5vZjKtjAAN0dsh+WEORucqMuepIAA66gDwXWPCWh+KP2yreXWdGsNWl0zwXBd2L31skzWs41GTEsRYHY4wPmXB4rvvGHxq8N+BvFdh4d1OLXH1G9WNomsNAvry3Adyi754YWjTkHO5hgYJwDmuV8R6P4t0X9pfTvFOl+FZde8PX3h6HRLq9gvreE2L/bGkaRkkYM6hGzhAScYr2agBM0teP8AxM+FXiD4hfGn4a69FcQaR4f8HXM2ovdQ30v2m+klhkia1NuFEYj5jcyM5PBUKMk17BQBwvxE+M/hz4X31jaa3Frckt6rPEdK0G91FAAQDva3icIcnoxFdwjh1DDOCMjIxTq8f+Ovwq8QfFnxH8O4LC5i0fRvD3iC28RXeqRX80d0WgLYtkgRdsiyhirM7gKM4Vj0APYK4r4kfF3QPhUlg2uxazIL0uIv7J0S81HG3Gd/2eJ9n3hjdjPOM4NdrRQBXsL2LUrC2vIQ4huI1lQSxtG+1gCMqwBU89CAR3qxXj37S/wq8RfGrwrpPhPRrqHRrKXU7a+vddF9LDdWK280cq+REiYlZwrL87oq5DfMQBXsAGAKAPJf2ivDh1nwza3UWneMNZubZpFisfCOqGyk3MmRJJ+8TcFKgD7xBb7p5qb9l7xJeeKfgX4XvdS1pte1NYXhu7yRWEglSRlaN9wBLJgKSRyVz3ro/iB8NE+ILWe/xL4j0BbdXVk0HUDaiYNjPmYU5xjgjBGT615v8Yf2eJta/Z8m+E3gCG20fT9RYQTald6jPHLYJ5nmtcoUVmnl3qDsZkDZ5bHB41Tn9YdTpa2+/wDXn8j6SeMw7yeODbvU5+ZabKzTV33un7u/2tke9V4r+0p8Vh4UstF8E6V4hsvDXirxfJJb2+q3s6RJplmgBur3LkDcisFjXPMskfYNj2KwtTY2NtbGV5zDGsZlkOWfAA3H3OM1Q13wfoPihoW1nRNO1doQRGb60jmKA9du4HGcDp6V2HzZ8/fsey6R8Xv2S9B07xRe23xB8t7uG+XW5l1ORyl5N5Pn+YWy21UI3dgCO1dH+w2Av7Jvw2AAAGmkADoB5sldL4Y+G+nfs7/CttF+HnhOXW/s8jumnxXEFvcXJklZmZ5n2Kdu9sbj91QB2rg/AXwj8Z6L+xZpfw3m0qwTxTPo0uk3dtd6o8ENsJjIrv58CuxKK+QE6kY3L1oA+jK8l/aB+Jnij4ff8ITY+ErTSrjVPEmsvpZl1gSNDbItldXJl2xspYj7OPlyN2SMrnI7L4W+DZvh18NfCvha41SfWrjRdLttPk1G5JMly0USoZGyScsVzyT16ml8ZfDzSfHV/wCHLzU/P87Qb59Qs/Jk2jzWtprc7uDkeXcSceuD2oA+c/h/+1p4o8R+CfEer+J28J+DJYtC0LX9OuroXE9tDFqJlCwzKrB5pf3OVWPbkyqmDt3G98P/ANpfx14+8JfFJdG0/Q9b8T+B7i1ljkeyvNKttVtpIRO6CG5Ikt5dqyKGcshba33ScdzJ+yL4HOiRadBPrNk1vZaLZ2l7bXoW4tf7KaRrKWNtuPMUyvkkEN3FKn7JnhF9J8YWF5q/iXU18YT2k2vz3uqF5tQW3G0RO+0FYnX5XRNoK/KNo4oAvfs8fGq8/aB0jVPGWn2ltaeAbiYW+gO4YX10IxtuJphu2ovm7kRMbsRlicMBXcfEbxovw98HX+vtZf2iLTZ/o3223tN+51X/AFtxJHEv3s/M4zjAySBVLwX8J9C+HviTxJq2grcafHr8sVzd6XHIBZLOiBDNHFj927qqhypw2xSRnmup1LTLPWLOS0v7SC+tJMb4LmMSRtg5GVIIPIBoA80+Dnx2j+LuoalapoX9kGyiWUv/AG7pmob9xIxts7mVl6dWAB7Guj+LvxQ0j4NfDvWfF2tMfsenxjZCpAe4mdgkUK543PIyICeAWySACa3NG8J6J4dkkk0nRtP0ySUBXaztUhLgdASoGas6to1hr1jJZanY22o2cmC9vdwrLG2DkZVgQcHmgD5R/Y/8aate/G74s6T4n+IVt4t1e5ttH1JLS21RbiztZZY7h7iCyjDkCKL93GSoydgZuWr66rgPCHwK8F+BPH3iDxhomi2tjrGtRW0M5hgjSOJYVZVEQVRs3BzuwfmwM9K7+gAooooAK89+FP8AyH/iZ/2NDf8ApBZV6FXnvwp/5D/xM/7Ghv8A0gsqAPQq88+Ff/IzfFH/ALGgf+m2wr0OvPPhX/yM3xR/7Ggf+m2woA+Y/jZ461rx98dviX4J05vFt54g8PafYJ4a0zw7qlxpVpZPLA002qXtyhCbUZ40VZA+7yyqxsWYj6b/AGdPHGpfEr4C/D7xVrKhdW1jQ7O8u9q7Q0rxKXYDsCckexqh8Qv2dPDnxD8SXutyalrugX2p2CaXq39g6gbVdUtFLFYp8Ak48yQB0KuA7DdjivR9H0iz0DSbLS9Oto7PT7KBLa2toRhIokUKiKOwAAA+lAHI/Ez4z+G/hIdPHiBNYb7dv8n+ytEvNR+7tzu+zxPs+8MbsZ5x0NY3xq8feJfh34ZtPHeix6fqHhjS4Xutc0m/YWlzLakKfNgmkZUSWMAnypAA+4ruVgK9TrkvGnwv0D4h6roN54ggl1KHRZzd22nSzN9jefjZNLD92R48EpuyFLEgZwQAbHhTxLZ+MvDOla9p63C2OpW0d3ALu3eCUI6hl3RuAynBHBGa8i/al8P6X4qk+Euk61p1rq2lXfji1S4sr6FZoZl+xXpw6MCGGQDgjtXtd3dC1i3Yyx4A9a8g/aA8PeLtZtfAmq+HNDbxFd6B4nt9Wm02K6htpHgW2uY2KvKyrkGZeCaAPJf2mdeXSPiv4T8CWsWs2ugLoLz22i+FHa1mvJ1k8qCBXjK+XEihmPIUAc9AK1v2avEmt+I/ho6+IZpbnU9M1O70t555fNeQQvgbpMDeRnbu77c12nxK+H1p8S73QdX1hNU8N+IbG2/dz6ZeiG6tfMX97CZE3Kw7HGRxkGvOPi38DrjXvghJ8MvBUVvpdjfsIptSur+aOWyXzBK1wuxS00u8Z2lkBJ5bHFfNujUWLlNv3df0/I+ux+b5bWyKll9KnasuW7ts05uUk/76lFNau61skkez15X+0vo2ral8IPE95pfirVvC50vSb6/kOjukUtyY7aRkQylS8ahwCTGVY4xkZr06ztzaWcEBkaYxRqnmOcs2BjJ9zXM/Ev4c23xR8NzaHfazrWkWFwkkVyNFuxbtcROhR4pCVbKEMeOPrXWtGfnq0Z1/7O2oS3Xwi8L3t5O89xNothLLNM5Z5Ha2QsxJ5JJJJJ9a9B0xDJNLMRgEnH518/S/A3Uh+z34h+HXhfULrWzqFqdKhufEurSRtZW7w+UGWWGLcREApWMAbuQWANe3+CNDHgHwN4b8O3OozanLpWm29g1/cZMly0USoZX6/MxXcfc16MJxhTUpOyPRpJuKSM740p4dHwm8W3Hi3R31/wAOWemzX19pkS7pLiOFTKVQbly3yDHI5xyK5L9lfw54l8MfDS4tvEEN7YWcuqXNxoWl6nfC9u9O0tyDb280wZ9zL8xA3ttVlXcdtegeMNOsvGXhXVtCm1HUNMi1G2ktXvNKna3uoQ6kF4pV5RxnIYdDWd4y0/Ub34balonh2CLWdQksfsEaatqEtqJFZfLZ5LhEdwwUs2QuSR1Gchxr0pvljJNmzhJatHZ1jeM9P0zVfCOtWmtWI1PSJrOVLuyZdwni2HemOM5GR+Nc78CvhxdfCH4P+EvBl7rE2v3ei6fHaS6jPndMwHJGSSFGcKCeFArsdV09dW0u8sXmntluYXhM1rIY5YwykbkccqwzkEdDg1uQeFfseaRrNl4O1vUjY6hoXgLWbyHUfCGgaveC6vNP0+S2iYh2DvsV5C7rFvYoGxx90e/A56Vy8OhX/gz4cQaNoAl8RX+m2CWlode1JxJdlFChp7nY7bjjLPtJJycVzP7NXwlv/gf8GtC8H6nqx1m/sjPLLceY8iKZZnl8pGk+ZkTfsBbBIXJAzgAHpN5aw31nPbXEYmgmjaOSNujqRgg/UGvmz9j3Rp7uPxlq+kaJqHhz4Ra39mPhvw5rV0txJEyiVLyRY98nkwyN5eIi3VWO1d2D9Luu9GXJGRjIOCK5zwX4RT4ceCbTQ7K91bX1sIn8u41m9NzeXBLM+HmfqcnAJ6DA7UAeR/s0eG9J8I/FD49aRoWmWejaVbeJrLybHT4Fggi3aTZM21FAAyxJOB1JNfQNeI/Ajw/4x07xB8W/FHiDwsfDt14k1iC+07S7nUIZ2ZItPt7f55IS6rl4W9SAc4rV/Zy+FGsfCjw14lTXb5LjUfEPiG98QPYwXct3b6d9oKn7NDLKFZ1XaWyVXLO2ABQBt/Hz4hX3wm+C/jPxlplpBfahoelzX0FtdEiKV0XIViCDg+xrxfwT+0p8QZvizYeF/FmmeGLbS5NY1DQZ72wedWFxBpqaiJRvYhYljkWJs5LMC42D5a+hPiJ4E0z4neBtc8J61539laxavZ3P2d9knluMHa2Dg++K43UP2a/Bera3Nqd5De3Ek2o3upywtcfu3ku9PWwmUgDO0wKAADkEk5oA8u+Fn7UuueM/i7pXgw6p4b8S2mvaTfX1hq+i6NqFnb20tv5WBvuGKXcTCXO+Fl+76MDW98Ff2hvFnxY+Idx4NuND0vStT8IJLD43kWVpY0uyzLax2OGyVkVGmLPnYpVCN+dvQeEf2WPD3g/XND1iHxJ4r1HUdB0u40fSZdR1MSrY2sqIhSNNgTKiNMOVLHaNxbAxpeDP2a/Bnw91bwtqfh5L/TdQ0GzuLE3Md0S+pxTP5kovSQTOTKTLuOCHZiCMkEA9Smk8mF5MZ2qWxkDOPc8V4d4A/alh8d+MtP8AD6+FvsDXjsn2n/hJ9FutmFLZ8qC8eVunRUJ5yeAa9zZQykEAg8EHvWHp/gLwzpN5Hd2Ph3SbO7jJKT29jFHIhIwSGC5HBNAG7Xzj8OdN8QeFP2vvEmiap4213xXb3Xgy31UxanMq28ErahcRgQwRqscYCIi5ALHBJY5r6Ev5ZIIQ6HGGGfpXjkH7N1ho3xQX4ix+NPGd1rTIsEkdxqiNbvbCVpVtmQRAmIM7fLnPPWgD22iqEt683lpb/fcZJPamSx3luPMEvmAckUAJcA2N4so/1b9QKm1MeZZ7lOQCD+FKrpqVqw6MP0NRafLuV7aUcjIAPpQBbs3EltGR6YpLyMS20gPYZqiqz6bIdqmSI+lPeee+Xy0i2KeGY0ASaaBNZFHG5QSOfSmvpUIcfvCgP8ORzVy3hFvEqDnHf1qO6skusEkqw4yKAGS+TY2zKABkEAdyaTS4mitRu43HIoh0yOJtzEyEf3ulXKACiiigAooooA+c/FX/ACM+sf8AX5N/6GaKPFX/ACM+sf8AX5N/6GaKAPSv2d/+SA/DX/sW9O/9Jo68/wDHXi34k/Dn4w+CFuPFWja7onizxC2kxeErfSPJuLey8mWQ3S3Hms7tEI1MhKhDvwApK59A/Z2/5ID8Nf8AsW9O/wDSaOvN9B+CHxW0b40az47n8Y+ENZfUbkQxtqOg3T3Wn6UJAwsrZ1u1jjGBln2Eu/zNuwAAD6KrNk8SaRFqg019Usk1EkAWbXCCYkjIGzOenPStKuauPhl4Pu/FSeJ5/CmhzeJEZXXWZNOha8VlXapExXeCFAA54HFAHPan8Zbbwt8TIvCfijTJvD9pqbJHoOvTSB7LU5imXty4H7mcENtjf/WAZQk5UejV5l4i+DR8ffESHW/F+qjWvDWlSQ3GieF1g8u0huUGTdXPzH7RKG/1YICR4BCl/mHptAHi2uNqviD9qaz0P/hItX03RdP8Lw6wNP0+4EUNxP8AbnQ+aNpLKVUKRkcV6vfeJdI0u9js7zVbK0u5cFIJ7hEkfJwMKTk5PFeMeIfElr4R/a9sZ9St9RW21bwlBplpc22m3NxC1ydQciN5Io2WPhgSXKgDknFep6/8MfB3irW7bWdb8J6HrGr2wQQahf6bDPcRBGLIFkdSy7WJIweCc0AdNRXkHxM1Px/c/Gf4a6X4ON7b6BBczXXimSWxQ2Mtk0LiNRO/PnCVVwkeTh9zYAGfX6AM7VPEmk6HJHHqOqWWnySDKLdXCRlh7BiM1oAgjI5Fc34r+GnhDx3cW1x4l8KaJ4hntlKwS6rp0N00QJyQpkUlQSAeK4X45ah4+Ov/AA70j4eNeWlw/iC1udan+wJJYnSULC5jllfhGII2BPnJAxgZIAPX68n+P1/420Dw7ea/4c8VaL4Y0nSbGa8um1KwNxJPIgykYYuFVTjHQtkjFesV4r8e/gr4r+Lus6E+m+KdP03QdMYXD6NqOnNdQXVyGJV5QJF3qo24Q8ZGTnjHLieb2TUE2/J2/qx7uR/V1j6bxU4xprVuceZWXS1nrLZNqyvfod/8KfFGo+Nvhr4Z1/V7D+y9T1LT4bq4swCBE7oCQAeQOc4PPNdXXg3xmn+LOkfC/wAPaD4Q1CS++JN1qNsG1aw0hV04QJcIZ/P8wssKeSx7l2K4QZPHvAzgZ61vC/Kr7nl4pwdeo6aSjzO1r2td2teztba+tjyT9pDxNeeC/CdrrafE/TvhdpsEjJcX2oaSl+LlypaONQzjH3HJCgs3YjHO58APGmu/EX4L+D/E3iW0tbLXNU0+O5uYrJsw5bOGXltoZcNtJJXdgnIrQ+INn46vUtE8GX/hyxUhxdHX7Ce6znGwoIpo+nzZBznI5HfxzxZ4A8Y/Af8AZZ/4Qn4Y3up6n4/mlkOnalZ6bE0YvJ7lriVpEfMVvbkvIvzHCKQBubGbOY+k689+NfxIu/h74Xgi0O0i1Xxlrdwul+H9MkbatxduCdz9xFEivLI3ZI27kV3VgtwtjbC7ZHuxGomaMYUvgbiPbOa4b4kfAzwv8VNc0bWdZbV7fVdIingsrzR9Zu9PkiSbZ5g3QSITu8tM59KAOM/Z78SeIfjt+zLoOreKNbuLPxBfG5W61LQMWblobuWMFBhgoIjAI56mtX9kXxVrHjf9m7wHrmv6hNqusXliXub24IMkzCR13NgAZwBWP8Gfhjo/7HnwQk0/VNb1bWoIJ5Jbi6VLy/8AmlmcoIrcGVkGHUMEGCcueSTXK/BOfxH4Q/YL8PQ6bp+t2Xi06HNb2EFpphlvLe7kaUQsYJAAMMVJ8zCgcsQKAPqGvOvjN8ZYPg9Z+H2Ogap4lv8AXtQbS7Gw0ryvMeYW0043GR1VV2wMCxOBnJ4Brd+FsXieD4a+FY/Gs0Nx4vXS7YaxLbgCNrvy184rjjG/d0wPQAVk/E/4ZS/ELWfA99HqC2I8OatLqbI0Rfzw9jdWuwHI24NyGzz93HfIAOI+HX7Vdp8VNE1++8O+CPElzdafYafqtnp0/wBlgm1G0vN/kzRmSZVRcxS58xlO1QwB3Ciw/astJvCHjTVbzwXr9pqvgu4gTX9Cha3uri2t5UWQXMbRSsk0axMXIVt2EcbcgA8RdfsWakfBh0aHxVZSuNG8L6W0N5YO9peDSHlZ47iNZFLwT+bhkDDAXq3StDwX+yn4p8EaT8To9G8V6D4Z1HxzPY75fDOgCxt9KgijMUy20PmMPMaMnbIx4YlyDwKAPX/hr8YtI+LOq+IF8NwT32g6TLHbJ4hQobK+nZA8iW7BiXEYZQzYC7iVBJVsdH4w8YaT4C8O3eua5ctaaXa7fOmSGSYruYKPkjVmPJHQVwvwM+CbfAeDWPDui6mJfABlW40PRpkZptKLAmeITFiZImkzIoIypdhkjGO88W+FrTxp4futHv57+3tbnbvk0y+mspxtYMNs0LK68gZwwyMg8E0Ac78O/jb4N+K15eWvhjVJdQns0WSZZLC4t9qk4BzLGoPI7ZrpvFHibTPBfhzU9e1q8j0/SdNt3urq6lOFijRSzMfwHTvXO/D/AOEWi/Da6u7jS7/xDeSXSLHINa8QX2pKADkbFuJXCH3UAmrvxL+Gug/FvwhdeGfEsE9zpFzJFLJHbXUls++KRZIyJI2Vhh0U8HtQB4/+zL8Y/HvxL+JPxM07xrYW+jWlhFpeoaRpCxBbixtrtJ3SO4fPzS7I42YdFZmUdK+ia8M+FH7LWnfCv4y+LfHNt4h17UY9YtrO3t7LUdZvboxeUjq5maWZhPncCm8Hy8ELjJr3OgAooooAK89+FP8AyH/iZ/2NDf8ApBZV6FXnvwp/5D/xM/7Ghv8A0gsqAPQq88+Ff/IzfFH/ALGgf+m2wr0F5FjGWYKPevPvhX/yM3xR/wCxoH/ptsKAOM/aj8RfEH4eeDdd8c+HPGmh+HtG8PaY14uk6ho5un1S6Uttt3l81SgkPlxoI137n6ngV7Rod7PqWi6fd3Vq1ldXFvHLLbMcmF2UFkP0JI/CvE/jJ8F/iJ4/+KWg+JNH8VeG00DQoxNp/h7xBo1xdwR3+T/pjeVcxCSRVOE3AhOSBuO4e0aONStdAsxrM9rdatHbp9rmsoWhgklCje0aMzMqk5IBZiB3PWgButeKNH8O+X/amqWenGXPli6uEiL4643EZ6iuL+Jfxnt/hf8A2Vqmo6RdXXg+XeNT16zPmDSvu+XLLEAWaE5bdIudmAWG0ll19b+GvhP4gLBceKvDOjeJHg3CA6vp8N15ION23zFO3OBnHoK5v4s/DSf4mRaVoFvrkui+EQHTWNN0qIxT6jFtCpbidWBhh+9vCDcwwoZRnIB3j6hbailhfWtxFd2M6LLFPA4eORDghlYcEEYIIryr9o3XNWkk+GmkaNrOo6DDrfjC3029u9MlEUzwGzu5CgYqcAtEh6Z+WvVdI8N2Wh+HLHR9OsrbTbGxhWC1tLWMRxQxqMKiqOAAABgV4r+01rX/AAjY+FGq3tpfTafpHja2u7x7Cymu3hh+xXqFzHErMVDOoyB/EKAOM/aU+JGpeAPFuh+ErLxhZ+ErWHQZdZ1XxTrFsL6YRRSx28UUcRKiSaWSTngk7SFXLDGn+zn8TNU+K/wwttY12z+w65bXl1pl9ELd7cGWCZoy/lOS0e4BWKEkqWI7VJ8bvhbJ8T/iJ4E+Jnhi50y113RbCVLRfEWlPcQSwXADBjHujkilQgFTkEbnUjnji/GHg/xl8J/2f73w/wCBL/UtY+I+qXk13HrFrp0bpLqFxcGeeWVXzHDCdzrlidq4A3NjPm1bOTS3OGpZtpHvtecfH7xB408K/DXW9Y8FNo8F3p1jdX1xdausknkxxQPIPKiTAkdioX5mULnPzY2n0GzWdbSAXLK9yI1ErIMKXx8xHtnNcZ8ZfCPiXx54F1Pw74b1XStIOq209jez6pZSXQ8iWJo28sJLHtcbsgncOOlYLfUxW56R8BNaufEnw40HV70q15qGmWd3OUXapkkgV2wOwyx4rstb6xfjXz9pNh8Qfht+zFreiWd9/a/je108aVoN34X0csySLAI7ZnimkdeGXLuzKgB6DFeyeHY9eh8EeGY/FMsM/iZNNgXVJbcARvdiNfOZAONpfdjHarxf+6P+up6+E3iZHjrTvEmraA9r4V1qz8PapJIg/tG8sftgijz8+yLegL9ACxIHcGuc/ZZ8ea/458N+J08QXtnrc2ia/d6Lb6/YW/kQarFDtHnrGGYKQ7PE20lS0TY9Kd8dvA3iv4j/AA9ufD/hDxPD4SvruZFur6W3eUva8+bCpjkRkL8LvVgwXdggkEVPBOleL/hT8Itc0/UH0q4axs1tdDtfAXh6aNrUbSiAQSTSiQhyrZJVQAS3GTXlYCyqR73PQr35We61meJ4PtXhzU4v7UuNEDW0gOpWmzzrUbT+8TerLuXqNysOOQa5T4Hf8JlZ/B7wivxKuoJfHH9nx/2tJHsUGcjJB2fLuAwDt+XIOOK6nxAv9qaDqVna3drDc3FtJDFJcKJY1dlIBdMjcoJGVyMjjIr6s8u55D+yp8Rte+IGjeKhqGry+L/D2m6oLfQPGM1iLNtatGgjkLlAiKxjd2j81FVH25A4Ne51w/hiGT4afCPSdPvHXVLrQtIgtZV8Pae37xoo1T9xbKWIHHCAnArI/ZrX4gj4N6E3xQnM/jJ2ne5aSKKKQRGZzAJFi+RXEXl7guQDkZJ5oGek3cJuLWaJZnt2dGUTRY3oSMbhkEZHXkEe1fP/AOzJ8Rda8e6x4/0b/hKLvx54L0x7ZdE8azWS2s1y0iSfaLfekaRTNCyJ+9jQD94AckV9CSBmjYKQGIIBIyAfpXEfCPwfdfCv4V6ToOq3Gn3U+lwSebNo9gbW3K73ceXAGcjAIGATk5PfFAHFfs932rweO/jF4c1DxBqniCx0DXrW10+TV5hNNFFJptrMy7goyN8rnp3r26vnz9nHX4dd8b/HTxTaWeqLo2oa/a3FnJd6ZcWslykelWkbmOKVFdvnjdeF5I4rq/2crr4gah4a8S33j+W4c3fiG9n0GO/tI7W7h0klfs6TRpwrj5+D820ruwcgAHXfFT4h2Pwl+HHiPxnqdvcXen6HZSX08FoAZXRBkhQSAT9TXl/gX9rfTvGfxBsPCNx4K8S6Bf3V3dad5+opb+VHdw24uhbkpKxLtbMsnAIUsFYhsgeifGz4dyfFv4SeLPBkV6umya5p0tit28fmCEuMbiuRnHpkV5nqX7Ll7f8AjGXW4vFJsGfXtU1lGtrciaH7Xo6acoRt3Dxsnmhsc8DA60Abvhj9oq41bx8ng7W/AWt+FdcvrG6v9IhvruynW/W32ebGWgnkEUg82M4fAwTzwRTvhz+07oPxS1/Q9D0LSNWfWLm3uJ9asp40jk8OGFzE0V6N3yyNKrIiruLbWYfIN1ec/CL9j3Wfhn468JeJzqPg6C58NaHd6RGmieHGs5NRklSIC6vJzM7yuWi3MP8AabByxNdd8Jv2bdY+E/jqHxbb+MX1bVddhkPjY3ludms3WS0FxCobFuYdzRKoypi2qeVDUAe8ySLFGzucKoLE4zwK8w8KftM/Dnxv4itNC0bXZ7rVLtikMLaVeRBiAWPzvEqjgHqRXpV5IkdtJvJ2kbflODz6HtXk/hn4E6L4O1+016z1DxbNPbMXSLUfFmp3lucgj54ZbhkYYJ+8pwcHtQB6zdx+bbyL7V873fjD4keCfjb4C0XV/FGi+JtI8Y319at4ds9HNtNplpDbySpdJN5rM4UrFHIXGC0w27eBX0TBMtzCHHGeo9DXzj8MPgn8UvBvxY1vxVqfi/wjr0+rXai+urjQroXyaerkpZ2z/a/LhRQeMRnLHc+480Ae/WSfZb9o27jANatUtSty8YlTh0549Kii1R2jGYWc9Mr0oAIR5GqNGvCsM4/Wn3ls/npNCMvnmls7d3ma4lG1z0X0q9QAnaloooAKKKKACiiigAooooAKKKKAPnPxV/yM+sf9fk3/AKGaKPFX/Iz6x/1+Tf8AoZooA9K/Z3/5ID8Nf+xb07/0mjrC8O/Hu+1z4/XPw4ufBGp6HaLpN1qlrrWpTxL9tFvcxQP5cClmEZMoKu5UsBkLgg1u/s7f8kB+Gv8A2Lenf+k0deT6nN8SZ/2tNK8WR/CfVH8MWWj3fhltR/tfTwHWa9t5BeCPzt/lhIWYqRv5AxmgD6apKWuIvPhTaXnj2PxWfEfimK4R0f8AsyHXLhNNO1QuDahvLIOMkY5PNAGjp/xI8Paj461PwbHf+V4l0+CO6l0+4ieJ5IHHEsRYASoD8pZCwVvlODxXTV4l8RPhf4h+MPxX0F9Rt4fDXhHwhexalZ6vZzA6rqdxsyYopF5tbcZ2yDlpcFcKvLe20AeUa5458X3P7QNj4I0SbRbPRYdDi1u/lv7Kae5mU3bQtFEyTIsZ2rkMyvyehHFer14t9pig/bInWSVI2fwJCqB2ALH+0ZOB612Pi34T2njDxPZa5N4j8VaZLarGostI124tLSTY5YeZCjBXJzg5HIAB4FAHcUV5N8TPjTeeC/i78M/BWladZa3L4nu7iPUYlu8Xmn2yQNIt0IQDmLchUs2BkqBkmvWaAPJPil8eJ/hx408NaCnhLUtRttW1Gz0+XWXYQ2cDXEhRQrEEyONrEqAMADJGRXrQr5+/aW03x/4q1fwrYeGfAza1p+i6zYa82o/2pBAJWhdy0ARyCD0+bpz04ra+KPx01v4fQ/C+1h8OWdz4l8Wa5Zade+HZNSU3dnbyhvtE8QUHzRAQCzcKFySRXJSnJ1akZXsrW0t669T6HH4ahTwGEr0lFTkpc1pqT0a5W43vG6vpZLTue0V5z8W/HXjjwZEk3hHwHB4ut4bWW8vbi71qPT0jVOfKjBSRnkYZIyFQY5cZr0avnb9qtfid4kuNH8J+FfBWo6/4Fv4nfxJd6Pq1rZXtxHkgWMbTSIY0kH+skXLbTtXaSWHWfPHs/wAOfHFh8Tfh/wCG/F2lpLHp2u6db6lbx3C7ZFjljV1DD1AbBroq8D+Jvxw1T4M/BXwvqNj4ItdO8S3d5ZaVZeA7nUYhcmNp0hMdv5O9ZGSNlbCZCrycYNe9jp6UAcX8S/EPjbw/a2sng3wppniZyJHuv7T1o6akKqAVCkQy7mbnqFAxyeaX4NfE21+Mvwu8N+NbOxuNMt9ZtRcizusGSE5KspI4YZBww4YYI61zH7ROkQeKvDlpoOofCrUPinpVy7SyWlne2tslvIq4QuZp4jgh3GU3YwcjpXn914v8V/sk/sd295rhsNe8Z6WhjsNFvNTZvO33BMFhFMV3zyRQMsa4UlzF6HNAH03XKfFH4i6f8KvBGo+I9RimultwsdvY2q7p725kYJDbxL3kkkZUA9W54Bro7CeS6sbeaaE28skau8LHJjYgEqfp0ryr41fBnxL8S/Ffg3XNA8bxeGH8NST3MNnd6QuoW8tzInlrOUMqfPGhkVSc481iOcGgB3ws+KniH46/AXSvGegWdh4S13UvNxaasr6hBbGK4eJ1by3hL58tsEEYJHXHOl+zj8SdS+MHwQ8I+MdYt7W11PV7Qz3ENirLCrB2X5AzMwHy9ya4n9j34b+M/gz8CLbQ/iBqlq15DPdSRWqQRxCzR7iV9rSLIwkLlt+eNu7b2zXM/s9eP4vhh+wD4c8UGbTY5tN0C4uLZdVuxbW806vKY4mk5xvYBRgEnPAoA+pa5P4jfFbwn8JNKtdR8XazDotndTm2t3lR3M0vlvJ5aKgJZisbkKBk4wMkgVJ8LvFOo+OPht4W8Ravo8nh/VNW0y2vrrSpWJa0kkjV2iJIBypJHIB45ANcf8cvAOreN/EPwwudNskvLfRPEE2oXpd0Xyozpl7CjgMeT5s0Q4yRnPQE0AWtO/aY+GOsaDr2tWHi+yvtM0LyPt9xbLJIIvO4hKhVJcOcqCgb5lZeqkB+l/tI/DbWPB954otvFVsNDsb2PTr25nilhNncSMqok6OgeHJkTlwowwOcc184+F/gp8Xfhp4Kf/hGdKk0/Uh4W8HaTcxaXdWiXciWjXH9pxWzSExLNtlG13+UliQc8i94O+FfxL0vSPjtdXHgWbU7vx02nWel6d4s1q3vj5P2c28st66NjbGDvaNNxIAVS3UAH1dpXjjQtc8Ua14d0/UYrvWdFWFtRtogT9m81S0YdsbQzKN23OcEHGCM7ckiRIWdlRR1LHArwv8AZU+FfiL4FaLr/gXWITq+n2l2L2w8YyTK1xrImXL/AGpSxcTRFRHuPytGseMYIr0b4teAj8TvAGqeGxNp8BvRGPM1TTI9RtxtkV/mt5CFf7vGTwcHtQB1cV1DcEiKVJCOoRgcU6WVIInlldY40UszucBQOpJ7CvFvgB+zm3wR1XV7xr3w3d/b4UhxofhO20ZxtYn53iYmQc9D0612Hxy+G9/8XvhdrfhDT/EMnhiTVUSGW/it/PJh3qZYim5SVkQNG2GB2ueaAOQ+AP7TFr8ffFvjnTdP0C50zStANnLp+p3MuTqttcCUx3Cx7QY0YQllySWVlbjOK9rr5n+A/wAE/id4A/aC8feIPEfiXT9R8M6hYaXawmz0aK0F8YIZUUIizMYBDuAxgh9wxjbX0xQAUVDcXSWwUvnngYqF71pSVt13nu5+6KALlee/Cn/kP/Ez/saG/wDSCyrtdMZ5Ekd2LEtiuK+FP/If+Jn/AGNDf+kFlQB3GoW32iA4++vIrz34OzeZr3xODHLjxPz/AOC2xr0yvK/huTZeLfiZIo+X/hKeR/3DbDNAFb48fF3xh8HdJ1LxLYeCbHxD4P0bTzqOp3kmui0u1VSxkSCAwssjKihhukTcW2jmvVLS5TVNOhuEV0juIlkVZF2sAwyAR2PPSvnv9qfwRP8AFSFdEg+EV/4y1GK0Z9G8TLrFvYW2mXTniQv56zqY2SN8pE+cDGeRXuvhGw1HRvCWi2OtaiNV1e1sYIb3UNuz7TOsarJLjtuYFse9ADIEZpfs0khjUHp6ms/xD8QvDXgTXtA0XWL4aZda9JJBp8s8TiCaZQD5RmxsWRgSVRiC21toODVH4hfC2x+J/wBikm8QeJNENrvCt4e1mfT/ADd2P9Z5ZG/GOM9MnHWuQ+O3w38SfEbwta/D/SrSxn0TWYng1bXtZ23P9nwoFw0UDcy3LZJRiQqMpckkBWAPWNNLSzzSHO0nAz9a8++O/j3xJ4Ki8D2fhb+yo9T8SeJIdENxrFtJcQwRvbXExfZHJGS2YFH3gOTXd+E/DsPhHwzpWiW91eX0On20dql1qE5nuJgihd8kh5dzjJJ6mvKv2k5o4Nd+CckrrGg8fW2Wc4A/4l9/3oAw/jV8T9d8J+LPDfhXSNDtfFXjPUdMkv7gNd/2dYW8EG1Zp3kYSsimSRFRMMfm5OFJqH4MfFbT/jR8PdP8U6dA1ok8k1vPatKk3kTxSNHKgkQlXUMpw44ZSD3rjf2uvhLqPi74s+EvFdtoN7418OxaVNpes+HNN1KKze8iaVJoCxkZFlhEiHfGXXdlT8wBU8zLrusfstfs26xrl3pmjyeLrvU7rVYvDaXYjhaa6ui4srcquZHSNgoVF+Zk44rzaqTk7bnDUS5nY+j64P40/E29+FHgi912w8K6l4snt4Zp2trF44o4o4o2keSaVyBGgVT0DEnACkmu2s5pLizglliMEskas8THJQkZK/h0rzz9oRvEV38LNf0Xwz4WufFOoa3YXWmeXbXcFuLbzYHQSuZnUFQWHC5PtWC31MUtT2D4L+IB4s8F6drghNsNTsra+EBbd5fmxB9ucDON2M4rqtb+9F9DXzt4G+JmufB/9lDU9d1/w9b+Gte8MaOlrbaZrmqQCK+ngtVEYWWJnH71lKqg+YnAxzXtvh7Xb3xT4I8M61qWmSaLqOo6dBeXOmSnL2kskau8THA5QsV6DpV4vTCP+up6+E0lEx/HWs6/oegmfwz4dXxNq7ypFHZS3yWcSgn5pJJWDYVR12qzHjC+lT4A/E+5+J2leIf7S0Q+Hte0HVptF1TT1uRcxR3Eao+Ypgq70ZJY2BKqeSCARWL8fNa+IGifDq5b4Z6Cmv8Aiq5mS2jV54YxaRMDvuQJWVZGQD5ULAFmXPANYHwR1af4SfBnxLNrHhGbwCNKSW9N34t121mOq3cgZ5Li4uInYK0kpAYn+8AowAK8nARXtYt73PQrt8rR658R/wDj1sv99v5V5h4nvNX0/Q7mfQtNg1fVV2+RZ3V39liclgDul2PtABJ+6emO9avhLx9qvxS+C3gXxdrmhP4a1XWbNbyfSpGJMBZcgcgHBGGGRnDDNc/4+lePwjqSL4dufFaTxG3l0izlijkuI3+VwGldE+6STlhx05r7WHwnzdX4y1+zJ8Tr7x9r3i/TNY0NdB17w5cLYXsFvd/a7Zy8ccyNFNtTcNsgyCqlT1FfQNfJP7JPhG6+E938QNZ1HT4fh74JuljutO8O6jqaSpp21f8ASJ5JQzRxCVipKK7KNmc5YivaP2bfirq/xr+DeheMdb0OPw/f6iZ/9DhlaSJo0meOOWNmALJIqq6nHIYEcEVhLc66Xw6HpN1532ab7N5f2jYfL83OzdjjdjnGeuK8o+E/xa8QeLvFnjfwN4l0vTdM8X+F47WZ7rSrh7nT7qG5RzDIu4I6MDE4aNuRgEMQwNesy5ET7V3tg4XOM+1eTfsvfDO1+Fvwh0yxPhNfB+rTGSbUraa5gurqSXzHxJPcwoqzMV2ndjgEDtUmw/4IfEHxV4q8S/Ejw94tbR7i+8KavBp8V3otpLbRzpJZQXOWSSWUggzFeGxxXrNeEfAm+tv+FvftC3X2iL7MviSxdpt42Ko0eyyS3TAwea6P9nv4v6j8Z9B8UapeaVa2Fnp3iO+0jTb3T7r7Ta6paQsojuopMAMrEsuRkZRsGgDv/FXinSfBHhzUdf12+j03R9Oga5u7ybOyGNRlmOOcCuG8IftMfDDx74htNC0HxjYajq91HNLDaIHV2WLO8/MoxwCwB5ZRuXK80v7Tfg3U/iF+z78QPDOi2y3mraro9xaWtu8ioskjLgKWYgDPucV4ZN8HvGmm/FP/AISHQ9KtbeSLxZrGrW13LJH5Yjl8PRWdq7qDuK/aE2lcZABOMUAe5+Dv2lPhv4+1K+0/QvEsd5f2dq989q1rPFLLbocNLCropmUEgZj3DJHqKt6d8avCHim48KQaL4itL7/hKYJbrSDbbnN3FGoaRxgfKEBAJbGGIU88V85fCvwD8VdS+LvgPxl4s8PeJJv7B8Pana6pPreu2Nw9xfzRwEi1ggYJFEzxMFJK543KuMnW/Zu+Dnjb4T/F+88Uax4dsGg8cwTzalY2M6Y8JS+dJOlvBlsSQy+ZmXyxzOpfBUjaAfUE6S20sYmcvHuDZJrRS9tpzsSeKQt/Crgk03U7L7fYzQZAZlIBZdwBx3Hevmj4Qfsjv8P/AIgaX4hfUfB0rafI7mLTvAdnYXLbkZfluEcsh+bqByMjvQB9HW5+wXhiY/u36E15FJ8ZvFfhv40+GvC/irwRaaXpXim6vLLSdT07WxeSloInlDXEBhTyw8cecqzhSQCec17PfWn2mMYwHB4Jr5jPw01vxf8AtA+G/GWlfDG/+Huq6fqLy674s1DVbZ/7VshE0ZtUt4JpPMEjCFt0ips8vI+bigD6kIyMGo4beO3BCDGeTUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHzn4q/5GfWP+vyb/wBDNFHir/kZ9Y/6/Jv/AEM0UAelfs8cfAL4a/8AYtab/wCk0dZy/tL+BH8aJ4bW9vzK+qHQ11T+zLj+zG1EdbQXmzyvNyCu3d94FfvcVo/s8HPwB+Gv/Ytad/6TR18HaL8O/EmsaFpnwt17Wtdm8caL41jk0rwzYabc21jaQLq/2ubWLq5A2XO6AuyEuFUsFCGTJAB+mdFFcHe6F8RpPiFFfWvi3QoPBgkQvo0mhSPeMgUBwLr7SFBLZIPlHA4560AdrBfW1zPcQQ3EUs1uwWaNHBaIkBgGA5BIIPPY1PXzp4+0HUfEn7Q+l3Pw30+78P8AiXTGgXxV4qnhaPTbmxxuWykiIAvZirZRkIMGcmQZ8tvougDxXx/r+g3vx+8NeGn+Ftv4y8RwWEWrDxDNFZbtItvtRjEivMRJlXBfEWT3HNbvjX9o3wN4A8QXOj6tqNyLqzWNr6S1sZp4bFZPuGeRFKxZ/wBo9DmsFf8Ak9Cb/sn6f+nFq+cvi9oWt6d42+L/AIc1KbXUg8R3BvtG0rSNNkdtdmkhWOFHuVBCwwso3R/LnnJxxXnY2vUw8FKmtX/lf8dv+CfY8MZThM3xNSni5tKKTsnZu81FtaO/Km5W0Wl21FNn3fBFaTyi+hjheSWNQLhFG506gbu45z+NWa8ks/iFYfBTTfhD4G8Rxajcat4gjj0O3vbaDzLdLqG1DsJnyNu4I+3AOdp6AE163XfFtpNnydWMYVJQi7pNpPuk2k/mlf5nnXjb9oHwH8PvHGgeDtZ1xI/E2t3EFtaadbwyTyK0zlIml2KRErMCAzlQSDjODXftaQNcrcNDGbhVKLKUG8KeoB649q+X/wBsr4p+F/DWr/DzSLyS8Gr2Xi7Rdbu1tdKurjZYxTuXlaSOJlIXDfLnd7c16/42+PfhnwLoPgfW7yPU7rSfF+q2Wkafc2lkzCOS7B8h51ba0aE4BJGQWAx6UZHo9cD8TPjZ4e+FMsMWsW2uXkklvJeOujaLdah5FvGQHllMMbBFGR1IPoDXfV83/tb/ALQS/DwaZ4DsprvR9T8T28guPEv9lXN7b6PZ8o8oSGNjJOeVjj6Z+ZyFGGAPe9D1PSPGGk6T4h0yW21Kxu7ZLqwv4wGDwyqGV0bqAylTWrXiMPxe+HvwG/Zv8LeIdNi1a5+H2nRWOj2T29jJ58URkW1jeSOUI4UNjcSM+gOQD7aDkAigDkviD8TLD4cQWkt7pXiDVftG8hdB0a51Fo1QAsz+SjbByMZwTzjODVzwd4r8O/FDwrovirQriDWNHvohd2F55fY5GQGAZGHIIIBByDXC/tF+OvD3hnw5aaXrHj/Wvh5d6kzm11DQbEXNzLsXDRgNbzr/AMtFOAoYkDaetcP8JPiB/wAM8/sXaV4l8aeHL/TbHw3ZyebYabYMt21otyyQ3D27vlJHjKTSKzZUs+cEYoA+lKy/FHibS/BfhzU9e1u9i07SNNt3uru6mOEijQFmY/gOnU1dsryPULK3uoSTDPGsqEjBKsMjj6GvEf2k/C3xA8Yax4KtfDnhrS/FXhCyvG1LWtJv9W+wG8niKtaRsxikDRLJmVlx8zRxg8ZBAN+bx94b+N3wPh8U6B4THxM8PaoA8Gi3tvDF9pCTFGLR3e1AUZGOGwfl45xWh8CvEvhv4l/BjwprugeG4fD3h69thPZ6K1vEi2YV2AUJH8i4IJ+XivMf2Bm8Txfs16VZ+JPDq+H/ALNcXwtc3RkknRrudmZ0KKY8MSoHO4ANxnFWP2T/ABRb+Cf2IvCXiG7tru8tdJ0K4vpbexi82eVI3ldljTI3MQpAGRk0AfRlMlmjgXdI6xr6scDpmsL4feONM+JngXw/4t0UzHSdcsIdRtPtEeyTypUDruXscMMjn6mvHv2svBtt471D4SaTqGmvqukP4ome9tdjPE8a6TflRKBwULhAQ3ByAc5xQB779pi2ufNTCfeO4fLxnn04pI7qGWJZEmjeNjhXVgQT6A1+cngPTv8AhWPwu11rrwaut6brHhXwPLq0ev2Vxd2q3E73P2q+u41Bkm8r92XQc4RFO1Rxo/D230VPh/8AtCadf6LdX/hS9vtJfw3p/hHQbrRo57+SACKXTbeVmaFjPHG3mg7MpvPynkA/Q0OpcoGG8DJXPIFOr5v/AGQbPWdKu/G9l8RIZ5PjGLqF/EGpshNrfW2zFm1m+0L5CxgqUGCsglLDLAn2L4r2Gvan4C1O28MLO+tuI/s4ttSXT3OJFLYnaGYJ8uf+WbZ6cZyADrqK8W+Afh74jaLqmrP43iv47Z4UFt9s8Ux6uC+47sKtlb7OMc5bPoK6r482vjm/+FOvWfw4+yr4uuo1t7WW7uPIWFXcLLIr7WAkWMuUyCNwXII4oAd8Pfjj4N+KfifxdoHhnVf7T1DwrcpaapsidY45WLgBHICyYaKRSVJAKkV2d9JJEiSRt8qn5h6ivkD9lPw54s8I/tBfEnQbr4c2fhHw3FpGhWubXWDdLbiGCcRBGMCeez5Yu2QVbk7i1fW0kf2YGCNzI8vAB/hFAEl1i8lt1AJjPzE1HLdTRgQCFULDChT0p9szWXmRSnEY5V6qlpFDzRhiP+erDnHtQBfEkWnwKhOWx0HUmuE+ETtJrnxLZk2Z8UNx/wBuFlXYwkZ/0dDLIesr9q4r4OzGXWfiVvOX/wCEnbP/AIA2dAHpVeb/AA0gFx4g+KaHv4oGD6H+zbCvSK88+Ff/ACM3xR/7Ggf+m2woAqfFP46+E/gD4UGt+NNROnWD3K2kOyJpZJJGBO1UQFjgKzEgYABJwBXdRxT6iFkdikTDIH/1q+Jf24vA3xN1q1+J/iCTwTpviLw7BocemeHrmHVSLiwR2ja7mFr5LF5pHCpkMMRxgD7zZ+1fBt5q+oeF9NuNe0uHRdXkhBubC3uvtSQt/dEu1d3GDnaOtAGrBAlum1BgUx762ivIrR7iJLuVGkjgZwHdVwGYL1IG5ckdNw9a5D4kaL4/1c2H/CD+KtG8NCPf9r/tbRH1Hzs7dmzbcQ7MYbOd2cjpjnzz9prRz4g0Xw3o+naJqOsfE53aXw7rGkBrP+yp1CiW7kuyrrDANy74m3+aCE2P2APea8n/AGi/EWg6L4e8N2Wu+AIfiS2ta5Fplhos8VrIv2loJ5Fk/wBJIjXCRSDdnPzY7mvQvClrrFj4Z0q38QX9vqmuRW0aX17aW5ginmCgO6xlm2AnJxk4ry39o3/kYfgl/wBj9bf+m+/oAofE74neH/hmvhex1DTbzT9Q1GySOw8NaPYteXKCNMyRpFbhhsiBALD5BwAeRlfB/ivQPiX4b0zxJok8WqaZcZktrhoirIwJRhtYBkdSGUggEEEGvI/2xjq3hv49+DvER1y88KeFLzw/daJqHiOw02S8nsS1xFN5ce1WELzCPaJWVgNmANxWsz4Ra/Yfs6fsya14r1nR9ctPDsGq6hrEGnvE82oQ2E94xhaRZGDbijLI+85G5ieQa82rH3m0cNSOrPo+uQ+J3xb8KfB3QBrHi3Vk0y0YssSBGlmnYKWZY4kBdyFBJwOACTgc11VpdR3trDcREmKZFkQkYJUjI4/GvLP2oPGGjeFPgx4qi1RphdarpN/p2npBZS3LyXElrIFQeWjFc9MnA96wSu7GK3PdPhpe6d4t8O2+qQIl3YXkcF9atNH/AAum9HwRwcMPcV0utdYvxrwb4A/GLQdG/ZbHi+OHU9Q0/wAL6DCNQtbawkS6321ohmjSOUIWIx1+6fWvYdJ8VWHjnwn4f8SaWZG0zWLGHULVpU2OYpY1kTcvY7WGRV4tWwjX9bnr4T4omJ438b6d4A0UanqcV/cRPMltFBpljNeXEsr/AHUSKJWYk4PbAxyRUvwr8feHPi9oF5f6T5l1a2929ld2eo2bwT2tzERvimhlUMjqSpwR3BHUGuT+P3xmt/gT8ObnxLLpd5rd00yWdlYWULyGW4fO3eUVikYCszPg4AOASQDzn7J/ijw7B8O/GOtWGrXvizXJL2fXfEd1Do9zZGe8kjyY7eGdEJVY4kjQDJIRcnJNeTgIfvIza6noV37rR7D8Rv8Aj1sv99v5V5n4j1+Hwxo1xqVxbX15FDtzBp1pJdTuSwUBY4wWbk9hwMk8Cug074maP8ZPhf4T8a6ALldH1qE3Vst5F5cyqeCrrkgEEEcEjjgkc1yHj/xJpvhPwjqOoatqs2h2Ij8ptRt4jLJbs/yK6rscEgsCMqR6gjNfaw+E+brfGbvwH+IXh34qXOvQ2KTs+nn7FqOmarYyW1xbSYRwssMqgjKsrA4wQeCa9H8fXc2naLC1rK9uwmVcxHbxtPHHbivmj9iD7UPGHxPv4bjUPEfh2+uILyy8U6tZG2vdUk8pUlQrsQPHEEjRGWNFOSADgk+t6H8XtF+Onwh0rxh4fgvrXTbu8lhEGpwCG4ikhklikV0BIBDo3c1zVXo2ergEvaQT7kf/AAkWqH/mI3P/AH9b/GsX4MfHPQvi74l8U6ToeqzeJDoJks9QtmDeS8uG+RWfCODtYbgSvvXIfGqx8X6r8N9VsPA/kr4gu9lusk1x9nMcLMBMySFWCyeXu2kg4Yg84rgv2I9L8S+HP2h/iNpl34ItPC2hx2emwxrbaiZ44PKtFSOOM+Uvmgrks2RtIwck5rjg23qz6TGKMYNRitt7H0R+zx4g8OauvjbQdJ+Glv8ADO70PU47PVdJigs0SaWS1imVybYlHzHKgyTnjHavYbeGK3hSGBEiiQbVjjACqPQAdK8I+B6te/Gz9oJEcpEPEtgWI7/8SiyFdr8K/iVovxaj8STaFHqVlJ4d1268P38Op2/kyLcwbd5UZOUYOjKe4boOldh8udrqLiS5jiZtkfViTirUTWrgRxtE2QflUg5wcH8jXjn7ZWm3V9+zN8SlsY55rt9CuY0S2BMhYrxtC85+lfNXhP4fW/w2+N9rrXhrwpeO1j4p1yygs7ZZAJLFPDsc6WyE8Kkt0ztno0rEnLUAfczXEFndF4Zo3jXiQK4Oz2PpU+pBQYrmN13HGDn73fj1r8+/gdqGkXnxz8E6xpWhaDoOh3nhbVh4jsvDfhW90y2t22W8n2W9mmJW7ljPmc7FYfNkfOBXb/sw6PcaP8WPD7+KdH1y38GXVje/8Kri1ZWf+y7RpXaaG5G3MU7w+UYfMJKwDy87gwIB9t284uIVcd+o9DTBZoLnzgSG9BSvB5VrIkC7W2naAcc49efzr51+GPhH4w6d4/0u58RwasuhpI5uGuPHEN9GF2NjMA02IvzjgSLjrk4wQD6RrgdS+OfgzS/i/pPwwm1Xd401K0e+h0+KF3CxKrNl3A2oSEchWIJAyBXcXjzR2kzW0ay3ARjHG7bVZscAnsCe9fA/h/wp8XvB/wC0F8HL/wAR/D7TLvxLf6nreoa1rdrrpkS7ea2jjdm/0ceTHBCqJFGSdwjC5BJYgH39RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB85+Kv8AkZ9Y/wCvyb/0M0Uvikf8VPq//X5N/wChmigD0n9nb/kgPw1/7FvTv/SaOvQq8K+A/wAavh5pHwQ+H1jfePPDNne23h+whnt7jWLeOSKRbdAyMpfKsCCCDyCK7r/hffwy/wCii+E//B5a/wDxdAHd0Vwn/C+/hl/0UXwn/wCDy1/+Lo/4X38Mv+ii+E//AAeWv/xdAHd0Vwn/AAvv4Zf9FF8J/wDg8tf/AIuj/hffwy/6KL4T/wDB5a//ABdAC+IPhBpWv/EjTPHH9paxput2VqliRp94Yobm3WbzhFMmDvXcTnpwcV3JUE5I5rhf+F9/DL/oovhP/wAHlr/8XR/wvv4Zf9FF8J/+Dy1/+LoA0tQ+GfhzVvHmm+Mr6wa91/TIGgsZ7i4keO0DBgzxQlvLSRgxUyBQ5U7SccV1NcJ/wvv4Zf8ARRfCf/g8tf8A4uj/AIX38Mv+ii+E/wDweWv/AMXQB3dcx4h+G3h3xX4n0LX9XsW1DUdDczaeJriQwQSkEeaIN3lmQAkLIVLLk7SM1l/8L7+GX/RRfCf/AIPLX/4uj/hffwy/6KL4T/8AB5a//F0Ad3RXCf8AC+/hl/0UXwn/AODy1/8Ai6P+F9/DL/oovhP/AMHlr/8AF0AaXjP4ZeHPiDe6Lc+IbBtTGj3IvLS2luJRbecCrJJJCGEcrIyhlMittIyuDXU1wn/C+/hl/wBFF8J/+Dy1/wDi6P8Ahffwy/6KL4T/APB5a/8AxdAHd1y/j/4aeHfijptpp3iewbVdNt7lbr7C9xKkEzr90TRqwWZAedkgZcgHHArM/wCF9/DL/oovhP8A8Hlr/wDF0f8AC+/hl/0UXwn/AODy1/8Ai6AO6ChQAAABwAO1LXCf8L7+GX/RRfCf/g8tf/i6P+F9/DL/AKKL4T/8Hlr/APF0AdL4o8PjxRos+nHUdQ0oSlT9q0u4ME64IPyuOmcYPsTXI2HwE8H2PwjsPhp9mvZvCNnEIBam/mjkljDFikkkbKzqxJ3KThgcEEcVZ/4X38Mv+ii+E/8AweWv/wAXR/wvv4Zf9FF8J/8Ag8tf/i6AOz0/T7bSbC2sbK3itLO2iWGC3gQJHFGoAVVUcAAAAAdMVYrhP+F9/DL/AKKL4T/8Hlr/APF0f8L7+GX/AEUXwn/4PLX/AOLoA7ukrhf+F9/DL/oovhP/AMHlr/8AF0f8L7+GX/RRfCf/AIPLX/4ugDu6QMGGQQR7Vwcnx7+GGxg3xF8JkY5A1y2/+LrKh+PHw7XMMfxF8KIjNnc2t2vH/kSgD0GW9e1u3DnzEIyAO1KFub4gsfJi9B1NcG/xo+FwjAPxI8KGRiPm/tu2P/tSrx+Pfwyii5+I3hRio/6Dlrk/+P0Ad6BgVncxXUghVpZj1Z+i1xlj8fvhzIrNN8RfCQGeB/bdrn/0ZVn/AIX18Mef+Li+E+f+o5a//F0AdO6qWIdjdTsMYXoKS0gMsjQzs2IxwmeK4qL46/DSzuHUfETwoInHDjW7Xj/x+mQfHb4bqz+V8RfCZZj80z65a/oPMoA7p4DbKUe42Qk5Cr941578LHa11/4iyqhSP/hKHBVjzj7BZVZX46/DRXPlfEPwnLL3lk1y1wPp89Vfghf6Z4ouPiHqOn6ha6zYT+JnMN7ZTLLDIPsNmCVdSQcEEcHqDQB6qrB1DDkHkGvPvhX/AMjN8Uf+xoH/AKbbCvQURY0CqMKOwrxjwf8AE7wd4N8bfE+x1/xZoeh3reJFlFtqWpQ28hQ6bYgMFdgcEg89ODQB7TRXCf8AC+/hl/0UXwn/AODy1/8Ai6P+F9/DL/oovhP/AMHlr/8AF0Ad3SVwv/C+/hl/0UXwn/4PLX/4uj/hffwy/wCii+E//B5a/wDxdAHd1x/xK+F+lfFKx0i31S51Cyk0nUU1SyutLujbzw3CxyRhgw7bZXGPeqn/AAvv4Zf9FF8J/wDg8tf/AIuj/hffwy/6KL4T/wDB5a//ABdAG8/hG3lhto5Lq6maCFIPNlkDSSBRjc7EcsepPc1zHjf4D+FPiPY2tj4jt7nUtPt7hbn7G1y6QSuvQSxqQsqg87HDLkA44qz/AML7+GX/AEUXwn/4PLX/AOLo/wCF9/DL/oovhP8A8Hlr/wDF1m6cG72IcIt3sbQ8FWIAAknAHYEf4Uv/AAhdkP8AlrP+Y/wrE/4X38Mv+ii+E/8AweWv/wAXR/wvv4Zf9FF8J/8Ag8tf/i6Xsodhezj2LXij4T+HvG3hq68P67Dc6ho906vcWn2uWFZwufkk8plLxnOGRsqw4IIrpP7Itkt7e3hjW2t4EEcUUKhURQAAoA4AAAAArkf+F9/DL/oovhP/AMHlr/8AF0f8L7+GX/RRfCf/AIPLX/4unKnCUeSS0NI+58J1f9jRf33/ADH+FZvibwJpfjDw7faHqv2uTTb1Qk6W13Lau6gg7fMiZXAOMEA8gkHIJFY3/C+/hl/0UXwn/wCDy1/+Lo/4X38Mv+ii+E//AAeWv/xdZQw1GnLmjFJmjqTkrNm0vgXR7bQtM0WwtU0vStNiWC0tLJFjjhjVQqoq4wAAAABVf/hXun/89rj/AL6X/Cs3/hffwy/6KL4T/wDB5a//ABdH/C+/hl/0UXwn/wCDy1/+LrrUmtjBwjJ3aNG5+HOmXul6hp809/8AZr6A28xt7t7aUISM7JYiroeOqsDWfofw50Lwz4bsfCOlWSaPodjgWttZgKqDn1zkkkkk8kkkkkmqt1+0F8N0ISH4heE2Y9zrlrgf+RKpXXxy+HkgV3+IvhFiP7uuWuR/4/UvXc0g/ZtOGljov+FZ6b/z8XX/AH0v/wATVvTfAtnpc7yw3N0HaNo928AgMMZBA4PpWFbfH/4aSwqX+InhNX6EHXLX/wCLqb/hffwy/wCii+E//B5a/wDxdQoRWqR0SxNaScZSdih8O/hHo3w5ufFUNpeavfXPiS4FzqF9qV+81xLIIUhUiTgriNEA24xjPWuo8CfD/QPhp4eTRPDmnrp+nrLJOymR5ZJZXbdJLJI5Z5HYkku5JPc1zd78bvhlcgMvxG8JLIvQ/wBuWvP/AI/Ua/H3wCE2/wDCwvCJP9465a//AByrOY71Z3fUHhYho9vTFNfSULEpIyZ7VxNn8cPhlb7nf4j+E3lbqf7ctf8A4urX/C+/hl/0UXwn/wCDy1/+LoA7O2sktuRln/vNViuE/wCF9/DL/oovhP8A8Hlr/wDF0f8AC+/hl/0UXwn/AODy1/8Ai6AO7orhP+F9/DL/AKKL4T/8Hlr/APF0f8L7+GX/AEUXwn/4PLX/AOLoA7uiuE/4X38Mv+ii+E//AAeWv/xdH/C+/hl/0UXwn/4PLX/4ugDu6K4T/hffwy/6KL4T/wDB5a//ABdH/C+/hl/0UXwn/wCDy1/+LoA7uiuE/wCF9/DL/oovhP8A8Hlr/wDF0f8AC+/hl/0UXwn/AODy1/8Ai6AO7orhP+F9/DL/AKKL4T/8Hlr/APF0f8L7+GX/AEUXwn/4PLX/AOLoA7uiuE/4X38Mv+ii+E//AAeWv/xdH/C+/hl/0UXwn/4PLX/4ugDu6K4T/hffwy/6KL4T/wDB5a//ABdH/C+/hl/0UXwn/wCDy1/+LoA7uiuE/wCF9/DL/oovhP8A8Hlr/wDF0f8AC+/hl/0UXwn/AODy1/8Ai6AO7orhP+F9/DL/AKKL4T/8Hlr/APF0f8L7+GX/AEUXwn/4PLX/AOLoA8w8U/8AIz6v/wBfk3/oZorkfEvxf8CS+I9VdPGvhx0a7lZWXVrcggucEfPRQB9X/wBnWh/5dYf+/Yo/s20/59YP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/s20/wCfWD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACj+zLP8A59IP+/Y/wriftHxS/wCfDwh/4G3X/wAZo+0fFL/nw8If+Bt1/wDGaAO2/syz/wCfSD/v2P8ACmvYWMYBa2t1zxzGv+FcK2o/E9ZxEbHweHI73t3/APGaq3178S5lEZsvCBkB423t2cf+QaAPRW06yUEm1gAHcxrTIbSwnUlLaBgDj/Vj/CvPIn+KF/y9r4RcLxt+23Q/9o1djf4nwgImn+D1HoL66/8AjNAHXr4dsjM0ksEUhJ4BjHFR6hp9nA0JWytjzgZiHFcx9o+KX/Ph4Q/8Dbr/AOM1R1Gf4nyPEhsfCAbqAL27/wDjNAHeXui2lxAQLWDcOR+7H+FUI9Phv9kJtYVVPvnyx/hXMWmofFGePiy8Hsy8H/Tbsf8AtGoZpfifZ3Am+w+EFD8EfbbvH/omgD0JNKso1Ci0gwOB+7H+FRQ29hNK8a2kIZeuYlrh31f4mqQq2Xg92PYXt3/8ZptuvxTWcztYeDwzdvtt1/8AGaAO4v8ARbSeBsWsG8cj92P8KgtdFtrqNXntoio4CeUAK5n7R8Uv+fDwh/4HXX/xmj7R8Uv+fDwh/wCB11/8ZoA7VdLslAAtIAB28tf8KnihjgTZGixr/dQYFcH9o+KX/Ph4Q/8AA66/+M1d+G3i7VfFEfiC31uzsrPUtG1RtOk/s+Z5YZMQQyhgXVSOJgMEfw+9AHZVBJY20zl5LeJ2PVmQE1PXmcHjLxx4i8SeKbPQNM8PjT9E1FdOEmpXk6yyt9mgnLbUjIA/f4xn+H3oA9D/ALMs/wDn0g/79j/Cj+zLP/n0g/79j/CuJ+0fFL/nw8If+B11/wDGaPtHxS/58PCH/gddf/GaAO2/syz/AOfSD/v2P8KP7Ms/+fSD/v2P8K4n7R8Uv+fDwh/4HXX/AMZo+0fFL/nw8If+B11/8ZoA7b+zLP8A59IP+/Y/wo/syz/59IP+/Y/wriftHxS/58PCH/gddf8Axmj7R8Uv+fDwh/4HXX/xmgDtv7Ms/wDn0g/79j/Cj+zLP/n0g/79j/CuJ+0fFL/nw8If+B11/wDGaPtHxS/58PCH/gddf/GaAO2/syz/AOfSD/v2P8KP7Ms/+fSD/v2P8K4n7R8Uv+fDwh/4HXX/AMZo+0fFL/nw8If+B11/8ZoA7b+zLP8A59IP+/Y/wo/syz/59IP+/Y/wriftHxS/58PCH/gddf8Axmj7R8Uv+fDwh/4HXX/xmgDtv7Ms/wDn0g/79j/Cj+zLP/n0g/79j/CuI+0fFP8A6B/hD/wOuv8A4zVe/vfilHBg2XhBNxxkXt3/APGaAO1nGnQkj7LC7Dssa0+2gsLoHbaQhh1BjWuHh/4WZaxZOn+D+mSzXt1/8Zqn9r+Jsc/nx2HhBUzji8u8f+iaAO6j060j1Vw1rB8w4zGP8K0P7Ms/+fSD/v2P8K8+uR8UbpVlSy8IbgMgi9uuf/ININa+J6Da9h4QDD/p9ux/7RoA6/8As+zsdQIFrCI36/uxxmtC40y3aFvKtoA+OD5a/wCFef7Pijes0r2HhABhhf8ATbvj/wAg1dSb4oogUWHhDAGOb66/+M0AdjaaXCkIEttAW/3BU39nWn/PrD/37FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sP/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AANuv/jNAHbf2baf8+sH/fsf4Uf2baf8+sH/AH7H+FcT9o+KX/Ph4Q/8Dbr/AOM0faPil/z4eEP/AAOuv/jNAHbf2daf8+sP/fsUV4ZqXxi+I+m6jdWjaF4VdreV4iw1C5wSpIz/AKn2ooA98ooooAKKKKACiiigAooooAKKKKACiiigAooooAp6xrFj4e0m91TVLyDT9NsoXubm7uZAkUMSKWd3Y8BQASSfSmaDr2m+KdEsdY0e+t9T0q/hS5tb20kEkU8TDKujDgggggivnr9tbxQbvQ/CHw0tdJ1XxBc+MtVjOoaZokaPdSaTass95tDui4cCKE5YDEx69D4fY/GDxH8KfgZ8VvA3h611b4f674X1/T7zw5DrVrCbiDR9T1KMIPLDSIyxu9zDwx+UIOD0AP0Dpa+PfHuvfFD4a+KPiH4H8PfEOfXr+Twlp+uaTf8Aip7K3ktruTUHtpoo5REkQMqKBGJFKrIVHIOK739mLxzq2peKPF3hfxDqnjBNYsLezvR4f8b2VoL2yjk81DJHd2v7q5hkeNtpwCpRgeoAAPoWivl74var48tviHq0ej+JPixY6crJ5Vv4d8J6XeWKfu1z5U00ZdhnOdx4OR0FfQPhaK51DwHpUV7dam15Pp0SzXV9EltfbzGAzyIgCxy5JJCjAbpwKALmneKNI1fWNV0mx1O1u9T0po1v7SGZWltTIu+MSKDlSy8jPUc1euLqO2XLnk9AOpr5j/ZS8BaR8NPj3+0LoGhxzpYwXuiSb7u5kuZpZJLDfJJJLISzuzszEk9TX0+8SSMrMoYr0zQBlXCz36+d5exFHHqau2kAhtg6x/vcZIbrmrE3+pf/AHTVTSX3W7DOSG5oAdYTpLG7bVRwSWAqCMHUL0yf8sk6UzUYDBKXUlY5OGxWlBEkMSqn3fX1oAkqobNmvhMzAqBwPSk1C5ktjGUI2k88c1bB3AEdDQBnTg2N4JV/1b8MKvSxpcRFW5U0ssSzJtcbh6U5VCgADAHagCKC0it/uLz6nrU1FFABRRRQAV578Kf+Q/8AEv8A7Gdv/SCyr0KvPfhT/wAh/wCJn/Yzt/6QWdAHoVeefCr/AJGX4o/9jQP/AE22Feh1558Kv+Rl+KP/AGNA/wDTbYUAeh0UUUAFFFFABRRRQAUUUUAFFFVbm/SAuv8AGBnGOKALVUZ7qSWcwW45H3mPanWIuGJklbKsOFqHTiI7qZG+8TQAPBdwDesxkxyR/wDWqxaXCXsY3KN6nkEfrVqsxF8jVdq8K3UfhmgBSDf3bxsSIo/4R3qa/CRWflgAZwFApk9hIs5lgcKT1Bp8Fk3mCWd/McdB2FADdOWeEtE6fIOQx7VdwPSlooAKxfCnjXQPHVldXnh3WrHXLW1upLGeawuFmSKeM4kiYqThlJGR1Ga4b9pz4m3nwm+CfiPW9It3vfEc0aabotnEMvcahcuILZFHc+ZIpx6Ka+ZfgZqH/DO3xIuPBlp4Y8SeEND8VeElksJPEEECefrmnWxW4kTy5ZAWmgCSNnGWhPXPAB920V8XfC/xn8SNL0P9nbxfq/xIv/ED/EO2aLWNO1S2tY7CEtpU95FJEI4leMo0ADEudwLHA4Aufs9fEjx1YfETwZpXxH8ReKINW8RWdyBDfQaff6BrkyxiZZdNvLQK0AVFdwkoO5D3IyQD7Forwv8AaIvfFFprGkDQNa+ImlwtA/mp4J0Kw1CJ23DBla5jYq3oFwMV1fwU1DVl+HUl1rl54r1W8jmmYyeKtMt7PUGQAEKIbdVQr12nGTQB2moeK9G0nXdK0W91S0tdX1XzfsFjNMqzXXlruk8tCcttUgnHQGtWvzk0T4qxeK/2uvg1478TaP4v03xNq15q1kukX3h7UIo9KsTbeXaW0e6ELI252lnlTIDSHJCIpr9G6ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAPnHxUT/wAJRrH/AF+Tf+hmik8Vf8jRrH/X5N/6GaKAPo+ivLf+GZPhx/0A7n/wb3v/AMeo/wCGZPhx/wBAO5/8G97/APHqAPUqK8t/4Zk+HH/QDuf/AAb3v/x6j/hmT4cf9AO5/wDBve//AB6gD1KivLf+GZPhx/0A7n/wb3v/AMeo/wCGZPhx/wBAO5/8G97/APHqAPUqK8t/4Zk+HH/QDuf/AAb3v/x6j/hmT4cf9AO5/wDBve//AB6gD1KivLf+GZPhx/0A7n/wb3v/AMeo/wCGZPhx/wBAO5/8G97/APHqAPUqK8t/4Zk+HH/QDuf/AAb3v/x6j/hmT4cf9AO5/wDBve//AB6gD1KivLf+GZPhx/0A7n/wb3v/AMeo/wCGZPhx/wBAO5/8G97/APHqAO2k8E6JN41g8XSaej+IoLB9MivmZi0ds8iyPGozgbmRSSBk7RzgVheN/gh4H+I+sjVfEfh+DU9Q+yJYGd5JELQJcJcpG21gCFmiRxnoR7nON/wzL8OP+gHc/wDg3vf/AI9R/wAMy/Dj/oB3P/g3vf8A49QB0Piz4QeDfHV5qt14g8P2mrzappa6NeG6BYTWaymVYiuccSMWBAyDgg8CoPht8FfBvwjOoyeF9INlc6iY/td5cXU13czhARGrTTO7lVBO1c4GTgDJrF/4Zl+HH/QDuf8Awb3v/wAeo/4Zl+HH/QDuf/Bve/8Ax6gD1KivLf8AhmX4cf8AQDuf/Bve/wDx6j/hmX4cf9AO5/8ABve//HqAO20fwTomgeI9f17T9PS21fXmhfUrpWYtcmGPy4iQTgbU44Arcry3/hmX4cf9AO5/8G97/wDHqP8AhmX4cf8AQDuf/Bve/wDx6gD0q/k8u1kI6kYH41n26vZGGUg7HGGGK4N/2YfhvIMHQrnH/YWvf/j1JL+zB8OJIig0O5HHH/E2veP/ACNQB6jPEtxCyHoRwaz4bmeBDAIi7qcA46V5xY/s0fD0oySaDdAocAnVr3n/AMjVZ/4Zl+HP/QDuf/Bve/8Ax6gD0SLT2kYSXL72/u9hV7pXl3/DMvw5/wCgHc/+Da9/+PUf8My/Dn/oB3P/AINr3/49QB6jRXl3/DMvw5/6Adz/AODa9/8Aj1H/AAzL8Of+gHc/+Da9/wDj1AHqNFeXf8My/Dn/AKAdz/4Nr3/49R/wzL8Of+gHc/8Ag2vf/j1AHqNFeXf8My/Dn/oB3P8A4Nr3/wCPUf8ADMvw5/6Adz/4Nr3/AOPUAeo1578Kv+Q/8S/+xnb/ANILOqH/AAzL8Of+gHc/+Da9/wDj1dj4K8BaD8O9Kl07w9YDT7SadrmRfNeRpJWABdmdixOFUcnoBQB0FeefCr/kZfij/wBjQP8A022Feh1574h+APgPxTrt9rOo6I8mpXzrJczQX1zB5rhFQMyxyKM7UUZx0UUAehUV5b/wzJ8OP+gHc/8Ag3vf/j1H/DMnw4/6Adz/AODa9/8Aj1AHqVFeW/8ADMnw4/6Adz/4Nr3/AOPUf8MyfDj/AKAdz/4Nr3/49QB6lRXlv/DMnw4/6Adz/wCDa9/+PUx/2avhpF9/Rp1+ur3n/wAeoA9HkuJYL4BzmJumB0qa5u1tsDaXY9FFeXXP7Mfw4ntyYtEuCRyCNWvDn/yNVbTf2afh1cO5k0S5ZlAxnVrz/wCPUAeppqTCQLLC0YPfmjVLbzYxKoyy9cdxXm9z+zB8OpYmC6Hc7scf8Ta9/wDj1Qaf+zd8OZ4yj6Hc719dWveR/wB/qAPV7Kbz7dGPUcH61XvrVxKJ4fvjqB3rysfs1fDuyvdjaJc+U/T/AIm17/8AHq0f+GZfhz/0BLr/AMG97/8AHqAPQl1N8bTA5f0FPs7aQzNcTDDnovpXnX/DMvw4/wCgHc/+Da9/+PUv/DMvw4/6Adz/AODa9/8Aj1AHqNFeXf8ADMvw5/6Adz/4Nr3/AOPUf8My/Dn/AKAdz/4Nr3/49QB6jRXl3/DMvw4/6Adz/wCDa8/+PUf8My/Dn/oB3P8A4Nr3/wCPUAdt4k8FaJ4wuNFn1mwjv5NGv01Ow8xmxBcqjokoAOCQHbGc4Jz1ANV/GPw88O/ED+yT4g0uLUm0q7F9ZO7MrQTbHj3KVIPKSOpHQhjkGuR/4Zl+HP8A0A7n/wAG17/8eo/4Zl+HP/QDuf8AwbXv/wAeoA6Oz+E3hKw0rwhpsGiQJY+Etv8AYkG5itli3e3G3J5/dSOnzZ4b15rA8Dfs1fDX4beJIte8O+F4NP1KBJY7VzPNLHZLIcyLbRO7JAG6ERKuRx04qP8A4Zl+HH/QDuf/AAbXv/x6j/hmX4c/9AO5/wDBte//AB6gD1Clry7/AIZl+HP/AEA7n/wbXv8A8eo/4Zl+HP8A0A7n/wAG17/8eoA7XVvBOia74l0HxBf6fHc6xoRnOm3TMwa285PLl2gHB3KMcg1uV5d/wzL8OP8AoB3P/g2vf/j1J/wzL8OP+gHc/wDg2vf/AI9QB6lRXl3/AAzL8Of+gHc/+Da9/wDj1H/DMvw5/wCgHc/+Da9/+PUAeo0V5d/wzL8Of+gHc/8Ag2vf/j1H/DMvw5/6Adz/AODa9/8Aj1AHqNFeXf8ADMvw5/6Adz/4Nr3/AOPUf8My/Dn/AKAdz/4Nr3/49QB6jRXl3/DMvw5/6Adz/wCDa9/+PUf8My/Dn/oB3P8A4Nr3/wCPUAeo0V5d/wAMy/Dn/oB3P/g2vf8A49R/wzL8Of8AoB3P/g2vf/j1AHqNFeXf8My/Dn/oB3P/AINr3/49R/wzL8Of+gHc/wDg2vf/AI9QB6jRXl3/AAzL8Of+gHc/+Da9/wDj1H/DMvw5/wCgHc/+Da9/+PUAeo0V5d/wzL8Of+gHc/8Ag2vf/j1H/DMvw5/6Adz/AODa9/8Aj1AHqNFeW/8ADMnw4/6Adz/4Nr3/AOPUv/DMvw5/6Adz/wCDa9/+PUAcF4qU/wDCUaxwf+Pyb/0M0V2T/snfCqV2d/Cxd2OSzajdkk+p/e0UAS2nxK+JF7aQ3EXwnJjmRZFz4jts4IyP4fepf+Fg/Ev/AKJP/wCXHbf/ABNegeGv+Rc0r/r0i/8AQBTv+Eh0o6r/AGX/AGnZ/wBpY3fY/tCedj12Zz+lAHnv/CwfiX/0Sf8A8uO2/wDiaP8AhYPxL/6JP/5cdt/8TXqVRR3UM00sUc0bywkCRFYFkJGRkdsjnmgDzL/hYPxL/wCiT/8Alx23/wATR/wsH4l/9En/APLjtv8A4mvUSQBknAqOK6hnlljjlSSSEhZEVgShIyAR24IPNAHmX/CwfiX/ANEn/wDLjtv/AImj/hYPxL/6JP8A+XHbf/E16lRQB5b/AMLB+Jf/AESf/wAuO2/+Jo/4WD8S/wDok/8A5cdt/wDE16iSACScAUtAHlv/AAsH4l/9En/8uO2/+Jo/4WD8S/8Aok//AJcdt/8AE16lTJpo7eJ5ZXWKJFLO7nCqByST2FAHmH/CwfiX/wBEn/8ALjtv/iaP+Fg/Ev8A6JP/AOXHbf8AxNeoI6yIrowZWGQynIIp1AHlv/CwfiX/ANEn/wDLjtv/AImj/hYPxL/6JP8A+XHbf/E16lRQB5b/AMLB+Jf/AESf/wAuO2/+Jo/4WD8S/wDok/8A5cdt/wDE16lRQB5b/wALB+Jf/RJ//Ljtv/iaP+Fg/Ev/AKJP/wCXHbf/ABNepUhIAyeBQB5d/wALB+Jf/RJ//Ljtv/iaP+Fg/Ev/AKJP/wCXHbf/ABNej6bq1jrNubjT7y3voAxQy20qyKGHUZUkZHpVugDy3/hYPxL/AOiT/wDlx23/AMTR/wALB+Jf/RJ//Ljtv/ia9SooA8t/4WD8S/8Aok//AJcdt/8AE0f8LB+Jf/RJ/wDy47b/AOJr1KigDy3/AIWD8S/+iT/+XHbf/E0f8LB+Jf8A0Sf/AMuO2/8Aia9SooA8t/4WD8S/+iT/APlx23/xNH/CwfiX/wBEn/8ALjtv/ia9SooA8t/4WD8S/wDok/8A5cdt/wDE0f8ACwfiX/0Sf/y47b/4mvUqKAPLf+Fg/Ev/AKJP/wCXHbf/ABNH/CwfiX/0Sf8A8uO2/wDia9SooA8t/wCFg/Ev/ok//lx23/xNH/CwfiX/ANEn/wDLjtv/AImvUqKAPLf+Fg/Ev/ok/wD5cdt/8TR/wsH4l/8ARJ//AC47b/4mvUqKAPLf+Fg/Ev8A6JP/AOXHbf8AxNH/AAsH4l/9En/8uO2/+Jr1DeN23PzYzinUAeW/8LB+Jf8A0Sf/AMuO2/8AiaP+Fg/Ev/ok/wD5cdt/8TXpFze+U4jjXzJD2HaoGuruAb5I1Kd8dqAPOrn4jfEqGFmPwoCnoCfEdt1/75qtD4w+I8i+ZJ8KGkZuefElt/8AE16jcsL6xJj5I5xT9OnE1uoJ+ZOCKAPMLbxp8SLVmK/CljnsfEltx/47UEvjv4k2l0Jx8KdqseR/wkdtj/0GvW7xzHbSMpwQODUFvGbvTwshJJzgn60Aecr8Q/iUygj4T5B/6mS2/wDiarN40+Ji3Qmj+FGM9R/wklt/8TXqtnC0EAR23EfpU9AHlbePfiSzAn4SgkdCfEdtx/47Tv8AhYPxL/6JP/5cdt/8TXqVFAHl3/CwfiX/ANEn/wDLjtv/AImj/hYPxL/6JP8A+XHbf/E16jRQB5d/wsH4l/8ARJ//AC47b/4mj/hYPxL/AOiT/wDlx23/AMTXqNFAHl3/AAsH4l/9En/8uO2/+Jo/4WD8S/8Aok//AJcdt/8AE16jRQB5d/wsH4l/9En/APLjtv8A4mj/AIWD8S/+iT/+XHbf/E16jRQB5d/wsH4l/wDRJ/8Ay47b/wCJo/4WD8S/+iT/APlx23/xNeo0UAeXf8LB+Jf/AESf/wAuO2/+Jo/4WD8S/wDok/8A5cdt/wDE16jRQB5d/wALB+Jf/RJ//Ljtv/iaP+Fg/Ev/AKJP/wCXHbf/ABNeo0UAeXf8LB+Jf/RJ/wDy47b/AOJo/wCFg/Ev/ok//lx23/xNeo0UAeXf8LB+Jf8A0Sf/AMuO2/8AiaP+Fg/Ev/ok/wD5cdt/8TXqNFAHl3/CwfiX/wBEn/8ALjtv/iaP+Fg/Ev8A6JP/AOXHbf8AxNeo0UAeXf8ACwfiX/0Sf/y47b/4mj/hYPxL/wCiT/8Alx23/wATXqNFAHl3/CwfiX/0Sf8A8uO2/wDiaP8AhYPxL/6JP/5cdt/8TXqNFAHl3/CwfiX/ANEn/wDLjtv/AImj/hYPxL/6JP8A+XHbf/E16jRQB5d/wsH4l/8ARJ//AC47b/4mj/hYPxL/AOiT/wDlx23/AMTXqNFAHl3/AAsH4l/9En/8uO2/+Jo/4WD8S/8Aok//AJcdt/8AE16jRQB5d/wsH4l/9En/APLjtv8A4mj/AIWD8S/+iT/+XHbf/E16jRQB4He/tGeMbC8ntpfhTP5sMjRvjX7UjIOD29qKp+KP+Rm1f/r8m/8AQzRQB7loUiQ+FdOkkkESLZRs0jHAUBBkn6V8A3Pwxs/hf8LWu/GPw203xz4QhuG17/hdvgHUoG1xYzP9oXUJBIvmllBG8xSSLsBwCOK/QHw4ofw1pasAym0iBB6H5BXi/wDwxd4EWzl0aPVPFUPgmWYzSeC49dmGjtl95j8nO4RFuTEHCdtuOKAOY134qfFHxg3xQ8UeCde8P6R4a8AXUtnBpOpaY1y+tSQWkVzM004lUwIwlCJsUkY3HIOK4Dwd8ZtRtPif468V6FFHbL4t8U+BLeSG7j3mO1vrCDzF6jDhZMA9iOlfQHjH9lnwd4y1rXb2S817SbTxEsaa9pGj6pJa2WrBEEY8+NemY1VGMZQsoAbIqx4h/Zi8D+I4fFCS299ZPr9xp15LNYXbQSWk9giJaS2zL/qmjEaYxkccjHFAHgP7XnxF8YeII/ix4O0zWLXR9P8AD1x4QuIJVtDLK/2u+ZZEY7143JC3uqsv8eRrS/FrxZ4d+JHjPwdocfh+38X614y0rw2niJ9LKoWOhpd3F5PEsgMrhYZFjQuAMopJCnPqkn7Ingi80nxlaaheeINVu/F0diurare6o73kr2jl7aVXAAR0YjG0BcIo24HOhf8A7L/g3VLDWIruXV5tQ1O/stVk1gag6X0N9aW6W8N1FKuCkmyMZI4bc+QQxFAHj3i348/FX4d6prngKfUdB1/xbY6x4bhsdfk057e3ubTVLqS3Int1kO2SNon5RwGUrwDmu28DeJ/ipqPi74m/DW/8WaHe+I9CtdK1HTPEw0QxJ5d00u+KW1ExDFfs7hWDj74JyRz1umfsxeDrGOeW7m1fWtXutY0/XLzWtUvmmvLq4snD2od8ACNCMCNVVcE8ZJNbeu/BTQtc1rxXrC3mr6XqviW0srO9vdK1B7aZY7V3eLynTBQ5lcMQeQcUAeeft8HVY/2TPHsmk6mNLuI7eEySiIuXjM0YZBhl25z154yMc1z+jfEX4qTfFnx/o914v8M2vhv4eabp93fT3ulm3GpyTWDyyb5fNYWsQdN5YK5CnHOOfffiP8PNG+KvgTWfCHiCKWfRtWtzb3CwymOTbkEMrjkMCAQfUVy+l/s8eE7Ow8ZWt8dR18eMNOg0vXJtWuzLJewxW7W67mAGGKMcsMEnng0AfOHhT9rfxfoPjfw62ta4njbw5reh6tqc7W/g+80W3t5bO0+1Ysric/6VGwVlyQTgq2RnFdB401P4v6v+zt4m8SeJ9f8AC2p+HfE3gTVb260e1sntJ9KeTTnlhS2l3v8AaQMlX3hTxuUj7tes6P8Ass+FdP8AEnhzXdR1bxH4n1Hw9BPZ6c2uambiOG2mhMMkJjChGVkIBZgXO1cscVSsv2PfAltYf2dc3XiDVtJt9Mu9H0vTtS1WSeDSLW5hMMqWoPKnymKKzlyq/KpA4oAw/wBkX4vax8YrO9lPl6F4f8O2VlpMPh69tWj1V5DbxyC9uA2PLikRgYkUHK5Ytn5Fzfi18SfipJ8Tfibovg7xFofh/SfBvhWy8Qr9v0hr2a7mkF4TAW81AkbC2GWwWHbvXs+i/B3w54d8bWnivTY7iz1eHR49ClaKYiO7tYyDCJ16O8Z3bX+8A7DODipL74R+HtR1/wAXazNHcG98U6TDoupETEK1tEJwgQfwt/pMvPuPSgD5+0L4/fEjQNT8J6n4q1jwrNpHjXwXqHii1tJLaSxttCmtoLeZElut7tJCVuMO5QEFNygD5ay/hl+0F4/8RfFXw34Sk8WRa/Z+L9F1Ge11aTwVd6Pb6feQRxuj2zXDD7XB+8OQecBTuG7Fe7eJP2afAvi7RvD+k6vYXF7p2iaBdeGraB7hgDZXEUUUquRgltsMeGyCCCRWRF+yn4cOtaZrd54m8X6prumWF1pdjqd5rBaa1triLy5EjAUIGwARJt35VSWOBQBx/wCy9+0J4w+Pvi/W7LUU0bSbXwSjaNr8NjKtw2pauHZWmt2DHy7QLGSpIJZnZc/ujmv+0z8ZviB8N/HJjs9Q/wCEN8F2+lJdweIpPC9xrlnc3peQPBePA++0iVViO/Yc72Ib5dteueEfgB4M8Aa94e1bw3p8miXGi6P/AGDFHZylY7izDBlSdf8AlqVfc6ufmDO5z8zZreP/ANn7Q/H3iO71w6z4h8O39/YrpupNoGpNarqFspcrHMuCMjzHAddrgMRuxQB5lbfFL4l/GXxb4ttfAHibwz4e0vwjY6fL9ol09tTi1u6ubNbv5X8yMx2wR0VWUF23FuMYrc8SfEbU/jL+xDqvjfRZl8MalrPg+bUvmi+0C3P2dmljX5lznDqr54yGwcYrZ1X9k7wTcy50e41zwfDLpdvot7beG9Tezjv7KBDHDFMBkkohKCRSsm043Yr0OX4eaC3w6l8DQWS2PhptLbRks7U7BFamLytiHthDgGgD5B8PeKvEXwm8AfDzwL4a8YaHoFy3he31drXwz4FuNV1C6ll4Qy2luSkEQVVUzO26Vw5+Tac9H8MPj58VPjzqfwytNE1HQfCaa14NXxPq802mPdkyx3ot5IYUMq7FkBJyxYoB3PNeyah+zP4YudXt9RsNU8Q+H5xo9toN5/Y+ptbjULKAMIY5iATlQ7gOhR8ORuq/8Mf2ePB3wiuNEl8OwXcTaPoz6BZi4uWlCWjXH2goc9SH6MecDFAHplFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUF6zJbOyHDAdaAKd6xtb1ZlO7I5XNW7SeS4VmZNin7vPWoYLeO7tUdxlyu3d3pmmytE728nBU8UAR2syRXVw8zANk4z9alNxNe5WFdkfQu1R6jbFJROF3LnLCrEepweWCSUIH3cUANt0hsXEW4tK/X0ps1hJHL5ts+0nqtJbq15d/aCu2NeFz3rRoAz/slxckC4kwg/hHer6qEUKowAMAUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHzv4o/5GbV/wDr8m/9DNFHij/kZtX/AOvyb/0M0UAe4aM/l+ErF/m+WxjPynB/1Y6Gvlrwj+1/cWnhL4c6N4e8Pv4g1nWPC8fiBV8W+KYbS6uojI8YhhmeLF3c5jYkBUABQkjdX1PocP2jwpp8Wdu+yjXPpmMCvnKX9kbxFafDDwt4Hg8ReFvEOh6XoK6Ncad4u8MjULbzVZiL23AmR45cPtKlmUhEI2kEkA9r8f8AxO/4QH4L698QLrR7r/iU6HLrMukTusc48uEymFmG5VfjaSMgH1ryOD9qD4hXniq08Lw/BqVPEGraSde0iCfxFAsLWSuqym6kEZ8iVTJCBGolBMg+YBWI72/+BCy/sw3Pwfg125kWTww/htNavl86U5tzD5zrkZ65259s1pWvwme2+K2geMv7SVl0vwvP4dNn5PMhknt5fN3buAPs+NuP4uvHIB53F+1Xq3ib4e+EfFXhLwKlzaa3pj6jc3PiPXIdJsrFkcxtbG4KP5k29XwAoXau4kZAqin7cfh+x8AeCfHmteHtQ0zwX4o0+5aLU43Fy1vqcLMBp7JGDuaXy5BFIpw7LtwMisHw3+xLq3gtvCk2neIfDeuXGjaHJooHinw6b+G1LXk1z9qtI/PURSnztjZJ3CNORjFXdG/Yahu/h14R+H/i/wAWT694O8N2t+0NnZwGzkuNQnmlaK9kdXPzQJKfLUAASEv2UAA9+0XxNrt58Nodf1Hwy2meIH09rxvDxvUZ45dhZbdpiFQN0Ut90EnkgZPA+DPjZ458R+I7PT9S+FEuiWM27zL8+J9OuRFhSR+7jkLNkgDgcZz0Fd94T8KajH8OLPw5411C18YXn2I2OpXkloI4tRQqUYyREsMuv3hnBJbgA4HP+HP2afhN4P1m21fQvhr4U0fVLbd5N7Y6PBDNHlSp2sqgjKkj6E0Acx4f+Ovj/VvEGnWF58H5dOs7m5jhmvT4r0yYQIzANJ5aSFn2g52qMnGBzXS/FvxfH4Y8Y/CuzdtSDax4hlskWxuxDExGnXc2LhSp82PERwgK/NsbPy4Mekfsu/B7QNXs9U0z4XeEdP1KzmS5tru20W3jlhlRgyujBMqwIBBHIIrU+JHwxbx/4l+H2rLqAsh4V1qTVjEYt/2kNZXNtszkbf8Aj43Z5+7jHOaAPIvhv+1/rfjaD4e67qPw2m0HwT42vv7KsNYbWIp547vy5WXfbhARExgkUPuzwCVAIrmvFf7SvjPx5b/DTWtA8JX+g+AfEHjjTLGy8RxaohmvLX7UUbz7UKGjhnCtt+ZiRt3Bdwr0fwz+zG/h/wCFXwj8Gtr63B8B6xBqrXX2XaL0RrcL5e3f8mfP65P3enNc5pP7K3jHR9P8E+E4PH9iPh54P8Q22tabYnR2OoSwwzmWK0muPO2FUBKh1jVjtTPQ5AKsP7dOlTakmq/2JYj4dvrX9hrrp1+3+37zcfZhc/2fjf8AZzNxu379vz7NtdXp/wC1I1/8Tx8Mx4Ru1+IMWrPBdaZ55MEGlKA41bz/AC8GFlZFVcBjK3l8YLVzXhf9kDU/Bd1Bouka74bg8FQa02qxPL4Yil1tIGnM7WX2t3KGPcxXzDF5gQ4ByA1bll+y7qNn8SYficPF7n4jvq7y3mofZ3+yT6O3yDSRB5nyxKio6vksJgZDncVoA9n8J6trGsWN3LrWhnQLiO9uIIbc3SXHnQJIVin3LwvmIA+w8ruweRXhviz9rHVPA/i+wg1zwNFpXhe91+HQIbu816GPVXaWcQR3S6ft3GBnYEESb9h37McV7n4VsdcsLG6TX9Vt9WunvJ5IJra1+zrHbtITDEV3NuZEKqXyNxGcDOK+W1/Yc1qLTU0iLxR4cS0i8TR+JH1pvDhfW9RKX4vFhu7sz/MAQF3KoJCJ0AIIB02qftf6zpT67rMvw2uP+EC0DxTJ4W1PXzq8QmWRbwWonhttmZIwzxlsspGWADbSa2NC/ajv/FXxZ1bwto3g+31DTNI1xtCv5k12BdVt2UhWu209lDfZgTw+/cV+YKRVjxB+zJJrnwg8beCB4gWFvEfimbxGL02pIgEmopeeVs3/ADY2bN2R1zjtWJ4//ZV1z4j+OLe/1nxHoV1pdp4gg1yy1RtAC+IrCOOZZhZQ3ySqFiyuzcYy2xip3H5qAPX/AIrfFjQPg/4bGseIJ7mCCVzBAbawuLwtLsZwCsCOyjCn5iAPfkV5b8KP2rz8WPghpvirw74fl8R+LUsLGfU9EiD6VDHLOuXEU94FjdVIfBV2yAOTkZ+gbm3S7tpYJATHKhRgDjgjBrjofgx4M/4VlpHw+vvD9lrfhLS7W3s7fTdXiW7j8uFQsW4SA7ioUcnnNAGR8LPif4s8c6xeWniD4eyeD7aGDzY7p9dsr/zW3AbNkDll4JOTxxiuC/bB134jeHND0HUPC2tWXh/w1DrmjR6lPEJG1G8M2pwQm3QjCxRbJMs+WZvu4UZJ9U8C/BL4ffDDUbi/8IeCPD/he9uIvImuNI02G2kkjyG2MyKCRkA49qi+NPwyb4t+CY9ATUBphXVdN1Lz2i8zP2W8hudmMj73k7c543Z5xigDu6KKKACiiigAooooAKKKKACiiigAooqrPqMUDleWYdQtAFhnVFLMQAO5pkV1FMcJIGPpVIsNTuAuSIlGSPei9shAomgypXkgUAEzz2MxkLGWJuvt/hVxZEu7dthyGGMelFvMt1AGIByMMPeqc1pJZyedbkle6UASaS+bdlPVWpupQMGW4j+8vXFM0qQNPMAMA8gVp0AUra+e6lC+VhMcnNT/AGSHdu8pN3ripQAOgxS0AJ0paKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD538Uf8jNq//X5N/wChmijxR/yM2r/9fk3/AKGaKAPdvDX/ACLmlf8AXpF/6AK0qzfDX/IuaV/16Rf+gCtKgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKiuLlLZQXzz0wKlpksKTLtcbh1oAcCGAI5BparwXUckrRKpXZwAeKsUAUtQuJrcoyf6sjB470un28Yt1cqGZxkkirE8QniZD0Iqlpspike3fgg5GaAI3X+zr1WH+qf9K1Dh1x1BFQ3luLmAr/ABdQfeo9NaQwbZFI2nAJ7igCvATYXhib/Vv0NadIVBYEgEjoaR13qVyRkYyKAKEYCaswXoRzitGq1rYpaksCWY9zVmgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD538Uf8jNq/8A1+Tf+hmijxR/yM2r/wDX5N/6GaKAPbNOuLiz8E209paG/u4tPV4bRZBGZnEYKpubhdxwMngZrwWx/ah+Jd/4/vvBqfAXUBrtjYW+p3MJ8UWG1LeaSWON92cEloZOAcjb7ivoTw1/yLmlf9ekX/oAryXw9pt5H+2T43v2tJ1sJfBOjQx3TRMInkW91AsgfGCwDKSM5AYetAHfaV8RbJrDULrX2svDS219d2qfa9SgZZY4HIM25WwoIwxU/MmcMAa0rXx14bvbrTrW38Q6VPc6jEZ7KGK9iZ7qMdXiUNl14PK5FfGGh/DZ/Efxs+H8eu+GZtQ0mH4keOb6VL6xZ7cK28wSOGXbtZsFCeCQCO1V0+DVh4Y+Ger3+jeC0sdbt/jXHcWlxbaaRcQ2i67GqtEQu5YBCXxtwgRm7E0Afbh8X6EviAaCda04a4U8waYbuP7SV67vKzux74q/f6ha6VZTXl7cw2dpCpeWe4kCRxqOpZjwB7mvzT0rwH4hM0/hPXtXvbX4lP42fUzbad4Ce41R5P7QMsV9HqzypH5HkhSXLALGGjxkbT9eftcaYbvw94Ev9R0u41zwbpPiq1v/ABLp9taPdmSySKcK7wIGaWOOdreRlCtwmcELQB69H428Oy+Hjr6a9pj6EBuOqLeRm2AzjPm7tvX3qSPxboUuk2+qprWnvplzkw3q3UZhlwpY7XztbhWPB6KT2r4q8UN4P1X4geGfHOlfD7U7f4LWPiaa8126/sudrPUbttOEVtqC6fs3iKKQeWZRFguQ/O3cMyH4eW3j3xvZX+neFLk/CXWfitpuo6VpdzpckFvIsWj3K3V39mdB5cElwqcsoV2BODu5APt23+IfhW7XTGg8TaPMuqMUsDHfxMLtgcERYb5yD125qebxr4et9Wg0uXXtMi1OeRoYbJ7yMTSOuNyqm7JIyMgDIyK+HPiZ8FNOs/hn+1Be6X4KSPWB4sspNGe10w+akaRadLutcLkDzXnYmP8AiL55zWR4ubwfqul/tL+FYvCN9qnxS8QeLLuDQLi20eaaSa5EFv8AZXiulQpEIJT5jZddgyx4bkA+1/Cnxe0zxHq/xCtLmNdGtvBuqrpd1e3k6LFJm1guPMycBFAuAvJ6qfWumsfF2hanY2N7Z61p13Z30nk2txBdRvHcPz8sbA4Y8HgZPBr4M+LHgnxdJqXi++niuIvD9j8ULHUdcnk0KTVYZLddBto0ujaAqbmGO52lgudpG7B8sim2nhQaz8N/igmkwav4tvPGOt6bD4Wl0/w03h6xj1mOPI1O1Uu7xJCVR5Z2RFYwEAuWOQD7k17x1DpOsaVY2yW1+J742l/IL+GI6cot5JhI6MwZs7FGxfmw+7G1Say/hJ8a/Cvxp8M2ut+HNQikhuZLlI7WWaP7RiGZonYorMQCQrD2dCcZr5X+HfhfUdOl+EHhrWtCv38Z6H8RL6TxhqE8DzR6nPNpOof8THzSoDwzq8YXsmREcbQK5Xwg9p8H/wBnnwl8SbLQLqw8R/CrxNqdv4h0wac9pNPZ3lzJFNHhkUS4SSzlVgWH7kAHjgA+/wCPX9LlvEtE1K0e6eSSJYFnUuzoAXULnJKggkdsjNcX8XvjJafCuPRLGDSL3xP4r8QXD2mi+HtNKLPeyIheRi7kJHGijc8jHAGOpIB4z4KeC9I+Gfh74a6N4q0/+0viNqCahqz6sdOaYw39z/pGoH7QFIhDNJsGWXeEUDOMVV/aAs9R8G/GH4YfFVdJvtb8OeHYNT0vWYdLtnurqzhu0hKXaQoC8io8AVwgLBZCQCAaAN7wJ8fNR1Dx5ZeCPHvgm8+HvijU7eW60mOW+hv7PUo4sGZYp4ukiBgzRuqnacjcAcdL4J+MWieMdDv9da5tdM0FdQurPT7+7ukRb+O3JWWdd2MJvSYDk5WMPnDceIeJPE//AA078W/h5f8AgCy1OTw/4NOpane+I7/TZ7GFriWyktoLWDzkRpXLTF32jaojGTkgVwvgbwfpvj/4Z/sYWk+gjWNH06SRdSt57XzoYLiDSrhH84EEAi5Qj5v4h60AfVfjT4v6L4R8I6d4sjnttW8LTX0Ftd6rZXKyRWsMr+ULjK5DosrRhsEbVZmz8uD3QOa+MPFWiWfgj4B/tgafJpP9laJNqV+ul2aW5hheS40mzVPIXAB33Ln7vBcnvmvrzwvb3dp4Z0iC/bffR2cKTse8gQBj+eaANSiiigAooooAKKjWdGmaIH51GSKkoAKQnAyar3N9HbcE7n/uimREalbHeCgyR8poAtggjIORVGxkea6nZmJA4A9OajNtc2WWhbzE67f/AK1R6bdxwNIJCV3HOe1AEuoRNBMlzH2PzVfikE0auvQjNIwS4iIyGVh2qjYM1tcvbtkjORQBfaZEdUZgGboKq31o8kscsP8ArAealmso5plkbOR6d6sUAIM4GetLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHzv4o/5GbV/wDr8m/9DNFHij/kZtX/AOvyb/0M0UAe7eGv+Rc0r/r0i/8AQBXlY/bA+E58QrpP/CTSBWvv7MGqnTboaWbrfs8kX3lfZ92/5f8AWYzxnNeoaHIIvCmnuyNIq2UZKIMs37scAetfCUmoR/Dv9mq98S+CfHPhv4gfBOCJ5/8AhXHjnTY1vI084u9glwjBhOshKpHNG53BQSetAH6B0V8P+KtVXXta/aU13U/iZ4i8MX3g4W95oWm2+uSWsWlE6RbzI5twwSUSTZQxyBlJVgBlyTy/xd+JHifxfo/j7Xo5/E9tq/hfw3ZXF/cHxefD2m+HNQbTluWSGCHMl5IWkUnzkKk4jBwDQB+hFFfF+geIZvjF4i8by+OviHrfhC18N+FNE1PTJdI1aTTUiFxYGe41J0jZRcYm3JiQNGBFt2/Mc+eeKviB498c6z8VdWt/EV2IPClrZnR9ak8YyeHItPgbTobhL+bTxCVnEzyO7CYMCAYgq7TQB+idFeB/H34ieK/Cn7I114qtL2PTfEr6bpxvNSsU3pZefJAl1cRhh0jSSVwWHG0EjivMPi9eWPweibQ/Cnxa8Rxwa3NokWsC91aXUZNIsLjUFgm1KO7mL+Q0it5eNwUf6xVG0mgD7Krn/CPgTSPBE2vy6VFJE+uapLrF75khffcyIiMwz90YjTgccV8VfH3Xtb+En/Cx/CPgLx54hl0mLQNF1T7Tca1NqF1ot9LrMNuBHcSM0iiaEuxiZiP3ZIADkHptZ+G91b/F34reEYviB49TQNH8HWfiKzg/4Se782PUZWvEabzt/mFf9GQ+Vu8rcSdh4wAfaFYdt410a78Z3/hSK83a/Y2MGo3FpsYbLeZ5EjfdjactDIMA5G3kcivjP4c6u/xi8WalL44+JniHREtvhr4a16O307xBLpkcdzPbTvc322N1BKsqEg5T5huU/Ljz7UvjN8QLXwJ4k8ei4fT/ABrf/DLwf9r1HCwNCk+qXkUt3ypERMTmTdtITduxhcUAfpTXmnxv8LeENY0zR9X8bXWpjRNH1C3m+wWs0/2W6naeIQC4giB85VlEbAMCoIyeM1806BJrugaz458PeJvFt34C8HP4Ml1e5lHj+41zUdMnjmURahDO6K8SMC4MZcq7IAFwWB5bTvjB488SfA/xt4p8U+JtY0L4l2up+GbCXw7C0ljHp1hLeWnl3CRBjlrtZJXdzyMmHgRkEA+99H8S6V4gudVt9Nv4L2bSrs2N8kLbvs84jSQxt6MEkjOP9oVp18KWul3/AMOdP+PHjfwtq2uzan4S+JCazfaYdYuJlvNNjtLRruJ4mcg5hmnIJGcwxDOI1A9j+D+pJ8XbXWviHqXjDVbDw/rfiyJvDFvBqjW0ElpZk28KKucOl1Ik0rIP9Yrxg52igD3LxX4s0bwN4c1DX/EOp22jaNYRGa6vryQRxRIO5J/IDqSQBya8i+DPxr+E9/4iuvDfhXVL/TtQ167uNZtdN1nTLvTlu3fDzvZi5iQSKzbpWWMnl3bGCaoftltDY+Fvh7rGrAHwdo/jbS7/AMRF13RR2amQLLKO8aXDW7tkYAXJ4FZ37W2v6P4n0f4baJoGoWeoeNr7xhpF74fSzlWWZFiuUkubldpJES2wm3v93DYJ+YAgHrmvp4V+JWvy+GL2c39z4aurLV7uyQt5KS5aS2ExxtYhoxKI85G2NiMFcstvjd4Kv/A+r+MLLXIr/wAM6RczWl7qVojyxRPDJ5czZUHciHJZxlQAWzgE15n8AvC2m/FD4ZfEq28U2rXn/CQeNNdi1e2MrxM6w3r20UTMpDBRBbwLjPKjHQ079lvw1pFv8NPiToEen2ttoS+NPEdiLCGJUgS3+1yJ5YQDAULxgDGKAPoJHWRFdGDKwyGByCPWnV4v+xjreo+Iv2Wfhre6rLJPdnSI4fOlzuljjLRxOSepaNEOe+c17RQAh4HrUNnc/aYixG0gkEVPVCz/AHN7cRdidwoAWf8Ac6jC/ZxtP+fyp90txLIEjISMjlu9JqiZgDjqjA1ajcSIrDoRmgChPaR2dpIw+ZyMbj71Z09dlpGPbNQau37pEHVmqw88dpEodsYGAO5oAklO2Jz6KTVDTraOe0IdQfmPPftUsU8l8kihNkZGAxqxbW4toggJPfJoAqx6c8MuY5mVD1FXtoBzjn1paKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigD538Uf8AIzav/wBfk3/oZoo8Uf8AIzav/wBfk3/oZooA928N8eHdK/69Iv8A0AVzEvwK+HE3jIeLZPAXhp/FAk84ay2kwG78z+/5u3du/wBrOfevAtD/AOQLp/8A17x/+gir1AHpWkfszeEF+JXjDxn4g0fR/E+pazq0Gq2Mmo6XFLLpjR2kFvtjkfceTAHyNuCRxxmuv1v4P+BPE3iZPEer+DNA1TX0j8pdTvNNhluAgBAXzGUtgAkDnjJrwaigD3bXvgz4B8UjRhrPgnw/qo0WNYtMF5pkMv2JFxtSLcp2KMDCjAGB6VJ4n+EPgbxrrdjrPiDwdoOuatYgC1vtR02GeaEA5AV2UkAHkeh5rwWigD6jubWG9tZba4hjnt5UMckMqhkdSMFSDwQRxiuU8O/B7wH4Q0XUtH0PwXoGkaTqeft1jZaZDFDdAjBEqKoDjBIwwPFeD0UAe76J8G/AXhrw5c+H9J8FeH9O0K5lWefTbXTIY7eaRWDK7oFwzBlUgkZBAx0rfk8NaRLqN7fvpdk99fWy2d1dNboZZ4FLFYnbGWQF3wp4G9vU1800UAegD9lXwRf/ABP1rxTrfh/Qdd06507S9P07R77SIZItMFmJwpi3AhQRMBtVQAEHXt6nL4U0Se6vLmXSLCS5vLRbC5le2QtPbqWKwucfNGN74U8De3HJr5sooA9w0X4G/Drw5ot7o+l+A/Den6VfSpPdWNtpUCQzujBkZ0C4YqwBGRwRxW1rPgHwz4ivnvdV8O6VqV5JDHbvcXdlHLI0UcoljQsyklVkAcDoGGRzzXzrRQB658TPhA/iLSfET+DJtG8GeKvEUSWeqeIzoyXNzcWoVkKnDIWcK3yM5YLj7pHFdJoXwy8M6B4O8M+GIdHtJ9H8OR2y6ZBdQrL9ma3ULDIuRxIuMhxyDk5r5/ooA+o7m2hvLeWC4iSeCVSkkUihldSMEEHgg+lcn4L+DfgL4cX91feFPBfh/wANXt0MT3Gk6ZDbSSDOcFkUEjPbpXhFFAHufgz4c/8ACEeMvGWqWV+TpHiS6i1JtMaP/j2vfLEc8iNn7sqxwsVxw6u2TvwJvGHgI6p4D8R+H/DM9v4UutaE3mahaWq7o5Jz+/nCgrmUhnIY/wAZBOcYPg1FAH0t4a8O6f4R8O6XoWk262ml6ZaxWdrbp0jijQIij6AAVduJGihZ0XewHSvlyigD6itZXmgVnUq3pVe5Hk30Eg6N8p/z+NfMp61Uv/ux/wC9QB9Xzx+bC6eoqHTnLWqg8Ffl5r5eqCw6Sf71AH1FqMEs08XlrkAdfQ0+HTlDb5mMr9eelfMg606gD6lAxS18s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQB9TUV8s0UAfU1FfLNFAH1NRXyzRQBveKP+Rm1f/r8m/wDQzRXzp4h/5D+pf9fMv/oZooA//9k=" alt="" />

    public int maxChunksToSorted(int[] arr) {
        if (arr == null || arr.length == 0) return 0;
        int res = 0;
        int curMax = arr[0];
        for (int i = 0; i < arr.length; i++) {
            curMax = Math.max(curMax, arr[i]);
            if (curMax == i) res++;
        }
        return res;
    }

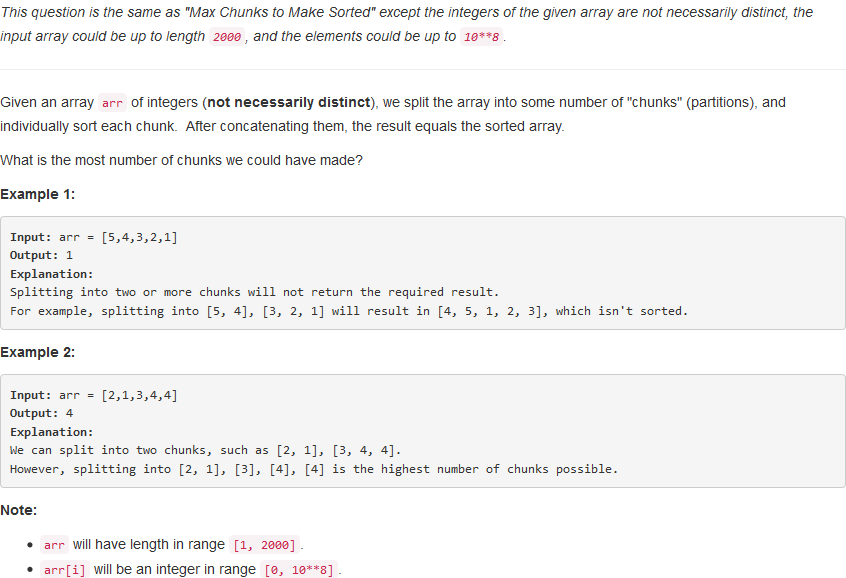
二、Max Chunks To Make Sorted II

问题描述：

问题求解：

本题是上一题的扩展，可以说是普通化的上一题，由于数字范围以及重复性，难度有了较大的提升，显然是不能直接使用上述的解法了，如果进行离散化，那么至少是O(nlogn)的时间复杂度，有没有O(n)的解法呢？

答案是有的，但是看问题的角度要变化一下，我们可以这么来看这个问题，从左向右遍历整个数组，如果说当前的数字的左边的最大值小于其右边的最小值，那么将这个数和左边进行排序是没有风险的，重复进行这样的操作就可以得到最终的结果。

可以使用两个数组来对左侧最大值和右侧最小值进行保存，整个时间复杂度显然是O(n)。

    public int maxChunksToSorted(int[] arr) {
        if (arr == null || arr.length == 0) return 0;
        int[] maxofleft = new int[arr.length];
        int[] minofright = new int[arr.length];
        maxofleft[0] = arr[0];
        for (int i = 0; i < arr.length; i++) {
            maxofleft[i] = Math.max(maxofleft[i - 1], arr[i]);
        }
        minofright[arr.length - 1] = arr[arr.length - 1];
        for (int i = arr.length - 2; i >= 0; i--) {
            minofright[i] = Math.min(minofright[i + 1], arr[i]);
        }
        int res = 0;
        for (int i = 0; i < arr.length - 1; i++) {
            if (maxofleft[i] <= minofright[i + 1]) res++;
        }
        return res + 1;
    }

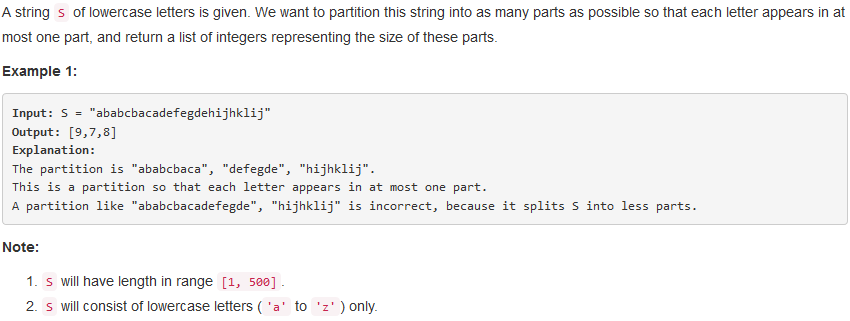
三、Partition Labels

问题描述：

问题求解：

本题的要求是将一个字符串划分成尽量多的子串，并且保证同一个字符只出现在其中一个子串中。

从直观上来看，我们可以暴力的进行求解，也就是对第一字符进行判断，将其最后出现的位置做标定，如果当前的idx和最后出现位置相同，那么就找到了一个划分，否则对第二个字符进行判断，寻找其最后一个字符出现的位置，并更新最后的位置，重复当前操作即可。

如果暴力检索，那么时间复杂度显然是O(n^2)，如果进行预处理，将一个字符的最后出现位置保存下来，那么时间复杂度就可以将到O(n)。

    public List<Integer> partitionLabels(String S) {
        List<Integer> res = new ArrayList<>();
        int[] map = new int[128];
        for (int i = 0; i < S.length(); i++) {
            map[S.charAt(i)] = i;
        }
        int begin = 0;
        int end = 0;
        for (int i = 0; i < S.length(); i++) {
            end = Math.max(end, map[S.charAt(i)]);
            if (end == i) {
                res.add(end - begin + 1);
                begin = end + 1;
            }
        }
        return res;
    }