topcoder srm 410 div1

problem1 link

不包含$gridConnections$ 的联通块一定是连在所有包含$gridConnections$的联通块中最大的那一块上。

import java.util.*;
import java.math.*;
import static java.lang.Math.*;

public class AddElectricalWires {

	static class UnionSet {
		public int[] father=null;
		public int[] size=null;
		public int[] edges=null;

		public UnionSet(int n) {
			father=new int[n];
			size=new int[n];
			edges=new int[n];
			for(int i=0;i<n;++i) {
				father[i]=i;
				size[i]=1;
			}
		}

		public int getFather(int x) {
			if(father[x]==x) {
				return x;
			}
			return father[x]=getFather(father[x]);
		}
		public UnionSet merge(int x,int y) {
			int fx=getFather(x);
			int fy=getFather(y);
			if(fx!=fy) {
				father[fx]=fy;
				size[fy]+=size[fx];
				edges[fy]+=edges[fx]+1;
			}
			else {
				edges[fy]+=1;
			}
			return this;
		}
	}

	public int maxNewWires(String[] wires,int[] gridConnections) {
		final int n=wires.length;
		UnionSet unionSet=new UnionSet(n);
		for(int i=0;i<n;++i) {
			for(int j=i+1;j<n;++j) {
				if(wires[i].charAt(j)=='1') {
					unionSet.merge(i,j);
				}
			}
		}

		int result=0;
		long visited=0;
		int maxSize=0;
		for(int i=0;i<gridConnections.length;++i) {
			int t=gridConnections[i];
			int ft=unionSet.getFather(t);
			int sz=unionSet.size[ft];
			result+=sz*(sz-1)/2-unionSet.edges[ft];
			visited|=1l<<ft;
			if(sz>maxSize) {
				maxSize=sz;
			}
		}
		for(int i=0;i<n;++i) {
			if(i==unionSet.getFather(i)&&(0==(visited&(1l<<i)))) {
				int sz=unionSet.size[i];
				result+=sz*(sz-1)/2-unionSet.edges[i];
				result+=sz*maxSize;
				maxSize+=sz;
			}
		}
		return result;
	}
}

　　

problem2 link

每个$base$的选择一定是$addresses[i]$或者$addresses[i]-k+1$。这样进行动态规划即可。

import java.util.*;
import java.math.*;
import static java.lang.Math.*;

public class ContiguousCache {

	public long minimumReads(int n, int k, int[] addresses) {
		List<Integer> list=new ArrayList<>();
		final int m=addresses.length;
		for(int i=0;i<m;++i) {
			final int t=addresses[i];
			if(t-k+1>=0) {
				list.add(t-k+1);
			}
			if(t<=n-k) {
				list.add(t);
			}
			else {
				list.add(n-k);
			}

		}
		int[] a=unique(list);

		final int p=a.length;
		long[][] f=new long[m][p];
		for(int i=0;i<m;++i) {
			for(int j=0;j<p;++j) {
				f[i][j]=-1;
			}
		}
		for(int i=0;i<p;++i){
			if(a[i]<=addresses[0]&&addresses[0]<a[i]+k) {
				f[0][i]=Math.min(n,a[i]+k-1)-a[i]+1;
			}
		}

		for(int i=1;i<m;++i) {
			final int r=addresses[i];
			for(int j=0;j<p;++j) {
				if(f[i-1][j]==-1) {
					continue;
				}

				for(int t=0;t<p;++t) {

					if(a[t]<=r&&r<a[t]+k) {
						long cost=f[i-1][j]+calCost(a[j],a[t],k);
						if(f[i][t]==-1||f[i][t]>cost) {
							f[i][t]=cost;
						}
					}
				}

			}
		}

		long result=-1;
		for(int i=0;i<p;++i) {
			if(f[m-1][i]==-1) {
				continue;
			}
			if(result==-1||result>f[m-1][i]) {
				result=f[m-1][i];
			}
		}
		return result;
	}

	int calCost(int p1,int p2,int k) {
		if(p1<p2) {
			if(p1+k<=p2) {
				return k;
			}
			return p2-p1;
		}
		else if(p1==p2) {
			return 0;
		}
		else {
			if(p2+k<=p1) {
				return k;
			}
			return p1-p2;
		}
	}

	int[] unique(List<Integer> list) {
		Collections.sort(list);
		int c=1;
		int pre=0;
		for(int i=1;i<list.size();++i) {
			if(list.get(i)==list.get(pre)) {
				continue;
			}
			++c;
			pre=i;
		}
		int[] a=new int[c];
		a[0]=list.get(0);
		c=1;
		for(int i=1;i<list.size();++i) {
			if(a[c-1]!=list.get(i)) {
				a[c++]=list.get(i);
			}
		}
		return a;
	}
}

　　

problem3 link

首先进行梯形剖分。对于变形每条边$p,q$，分别向$x$轴做垂线，该边与垂线以及$x$轴可以组成一个梯形。对于$n$条边$n$个梯形来说，注意有的取正值有的取负值加起来就能得到整个内部的点个数。

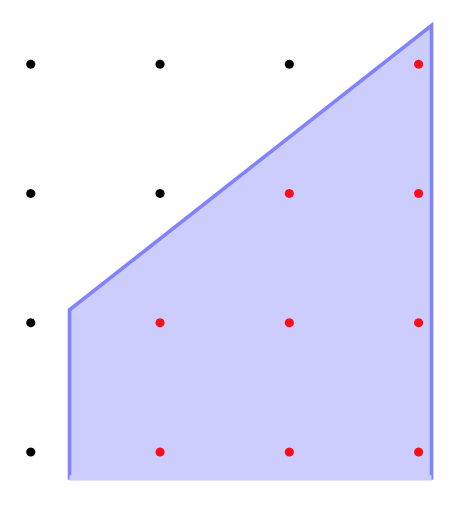
对于一个梯形来说，内部点可以用公式$\sum_{i=0}^{n-1}\left \lfloor \frac{a+di}{m} \right \rfloor$来进行计算。

这里可以认为$0\leq a < m,0<b<m$，否则可以直接提出到外面进行计算。

对于某个$i$，$\left \lfloor \frac{a+di}{m} \right \rfloor$的值可以看作垂线$(i,0),(i,a+di)$与水平线$y=km$的交点个数，$1\leq k \leq \left \lfloor \frac{a+di}{m} \right \rfloor$

到这里可以换个角度计算。对于每条水平线有多少垂线与其有交点。按照这个思路，可转化计算的公式：

$\sum_{i=0}^{n-1}\left \lfloor \frac{a+di}{m} \right \rfloor$=$\sum_{k=0}^{L-1}\left \lfloor \frac{(a+dn)mod(m)+mk}{d} \right \rfloor$,其中$L=\left \lfloor \frac{a+dn}{m} \right \rfloor$

中间的推导就不写了。

等号后面的式子跟前面形式类似，所以可以继续转化，每次求和项都在减少。

import java.util.*;
import java.math.*;
import static java.lang.Math.*;

public class WifiPlanet {

	public long routersNeeded(int[] x, int[] y, int denom) {
		final int n=x.length;
		long result=0;
		for(int i=0;i<n;++i) {
			result+=cal(x[i],y[i],x[(i+1)%n],y[(i+1)%n],denom);
		}
		if(result<0) {
			result=-result;
		}
		return result;
	}

	long cal(long x1,long y1,long x2,long y2,long m) {
		if(x1==x2) {
			return 0;
		}
		if(x1>x2) {
			return -cal(x2,y2,x1,y1,m);
		}
		long L=(x1+m-1)/m*m;
		long R=(x2-1)/m*m;
		long n=(R-L)/m+1;
		return dfs((y1*(x2-x1)+(y2-y1)*(L-x1))/m,y2-y1,n,x2-x1);
	}

	long dfs(long a,long d,long n,long m) {
		if(n==0) {
			return 0;
		}
		if(d==0) {
			return a/m*n;
		}
		if(d<0) {
			return dfs(a+d*(n-1),-d,n,m);
		}
		if(a>=m) {
			return dfs(a%m,d,n,m)+a/m*n;
		}
		if(d>=m) {
			return dfs(a,d%m,n,m)+(d/m)*n*(n-1)/2;
		}
		return dfs((a+n*d)%m,m,(a+n*d)/m,d);
	}

}