基于Python的机器学习实战：Apriori

目录：

1.关联分析

2. Apriori 原理

3. 使用 Apriori 算法来发现频繁集

4.从频繁集中挖掘关联规则

5. 总结

1.关联分析  返回目录

关联分析是一种在大规模数据集中寻找有趣关系的任务。这种关系表现为两种形式：

1.频繁项集(frequency item sets)：经常同时出现的一些元素的集合；

2.关联规则(association rules): 意味着两种元素之间存在很强的关系。

下面举例来说明上面的两个概念：

表1 一个来自Hole Foods天食品店的简单交易清单

交易号码	商品
0	豆奶， 莴苣
1	莴苣，尿布，葡萄酒，甜菜
2	莴苣，尿布，葡萄酒，橙汁
3	莴苣，豆奶，尿布，葡萄酒
4	莴苣，豆奶，尿布，橙汁

频繁项集是指经常出现在一起的元素的集合，上表中的集合 {葡萄酒，尿布，豆奶} 就是频繁项集的一个例子。同样可以找到如 “尿布 --> 葡萄酒”的关联规则，意味着如果有人买了尿布，就很可能也会买葡萄酒。使用频繁项集和关联规则，商家可以更好地理解顾客的消费行为，所以大部分关联规则分析示例来自零售业。

理解关联分析首先需要搞清楚下面三个问题：

1.如何定义这些有用的关系？

2.这些关系的强弱程度又是如何定义？

3.频繁的定义是什么？

要回答上面的问题，最重要的是理解两个概念：支持度和可信度。

支持度：一个项集的支持度(support)被定义为数据集中包含该项集的记录占总记录的比例。从表1 可以看出 项集 {豆奶} 的支持度为 $4/5$; 而在 5 条交易记录中 3 条包含 {豆奶，尿布}，因此 {豆奶，尿布} 的支持度为 $3/5$.

可信度或置信度(confidence)：是针对一条诸如${尿布}-->{葡萄酒}$的关联规则来定义的，这条规则的可信度被定义为“ 支持度({尿布,葡萄酒})  /  支持度({尿布})”。在表1 中可以发现  {尿布,葡萄酒} 的支持度是 $3/5$, {尿布} 的支持度为 $4/5$, 所以关联规则 “尿布 --> 葡萄酒”的可信度为 $3/4 = 0.75$, 意思是对于所有包含 "尿布"的记录中，该关联规则对其中的 75% 记录都适用。

2. Apriori 原理 返回目录

假设经营了一家杂货店，于是我们对那些经常在一起购买的商品非常感兴趣。假设我们只有 4 种商品：商品0，商品1，商品 2，商品3. 那么如何得可能被一起购买的商品的组合？

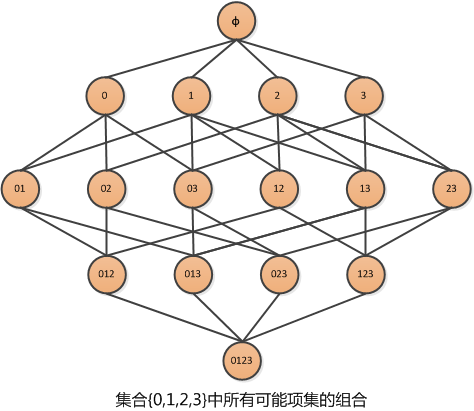
上图显示了物品之间所有可能的组合，从上往下一个集合是 $\textrm{Ø}$，表示不包含任何物品的空集，物品集合之间的连线表明两个或者更多集合可以组合形成一个更大的集合。

　　我们的目标是找到经常在一起购买的物品集合。这里使用集合的支持度来度量其出现的频率。一个集合出现的支持度是指有多少比例的交易记录包含该集合。例如，对于上图，要计算 ${0,3}$ 的支持度，直接的想法是遍历每条记录，统计包含有 $0$ 和 $3$ 的记录的数量，使用该数量除以总记录数，就可以得到支持度。而这只是针对单个集合 ${0,3}$. 要获得每种可能集合的支持度就需要多次重复上述过程。对于上图，虽然仅有4中物品，也需要遍历数据15次。随着物品数目的增加，遍历次数会急剧增加，对于包含 $N$ 种物品的数据集共有 $2^{N}-1$ 种项集组合。所以即使只出售 $100$  种商品的商店也会有 $1.26\times10^{30}$ 中可能的组合。计算量太大。

　　为了降低计算时间，研究人员发现了 $Apriori$ 原理，可以帮我们减少感兴趣的频繁项集的数目。

$Apriori$ 的原理：如果某个项集是频繁项集，那么它所有的子集也是频繁的。

即如果 {0,1} 是频繁的，那么 {0}, {1} 也一定是频繁的。

这个原理直观上没有什么用，但是反过来看就有用了，也就是说如果一个项集是非频繁的，那么它的所有超集也是非频繁的。如下图所示：

3. 使用 Apriori 算法来发现频繁集 返回目录

上面提到，关联分析的两个目标：发现频繁项集和发现关联规则。首先需要找到频繁项集，然后根据频繁项集获得关联规则。首先来讨论发现频繁项集。Apriori 是发现频繁项集的一种方法。

首先会生成所有单个物品的项集列表；

扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度的集合会被去掉；

对剩下的集合进行组合以生成包含两个元素的项集；

接下来重新扫描交易记录，去掉不满足最小支持度的项集，重复进行直到所有项集都被去掉。

数据集扫描的伪代码：

对数据集中的每条交易记录tran:

　　对每个候选项集can:

　　　　检查一下can是否是tran的子集：

　　　　　　如果是，则增加can的计数值

对每个候选项集：

　　如果其支持度不低于最低值，则保留

返回所有频繁项集列表

有上面的伪代码写出代码如下：

# -*- coding: utf-8 -*-
"""
Apriori exercise.
Created on Fri Nov 27 11:09:03 2015

@author: 90Zeng
"""

def loadDataSet():
    '''创建一个用于测试的简单的数据集'''
    return [ [ 1, 3, 4 ], [ 2, 3, 5 ], [ 1, 2, 3, 5 ], [ 2, 5 ] ]

def createC1( dataSet ):
    '''
    构建初始候选项集的列表，即所有候选项集只包含一个元素，
    C1是大小为1的所有候选项集的集合
    '''
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if [ item ] not in C1:
                C1.append( [ item ] )
    C1.sort()
    return map( frozenset, C1 )

def scanD( D, Ck, minSupport ):
    '''
    计算Ck中的项集在数据集合D(记录或者transactions)中的支持度,
    返回满足最小支持度的项集的集合，和所有项集支持度信息的字典。
    '''
    ssCnt = {}
    for tid in D:
        # 对于每一条transaction
        for can in Ck:
            # 对于每一个候选项集can，检查是否是transaction的一部分
            # 即该候选can是否得到transaction的支持
            if can.issubset( tid ):
                ssCnt[ can ] = ssCnt.get( can, 0) + 1
    numItems = float( len( D ) )
    retList = []
    supportData = {}
    for key in ssCnt:
        # 每个项集的支持度
        support = ssCnt[ key ] / numItems

        # 将满足最小支持度的项集，加入retList
        if support >= minSupport:
            retList.insert( 0, key )

        # 汇总支持度数据
        supportData[ key ] = support
    return retList, supportData

注：关于上面代码中 "frozenset"，是为了冻结集合，使集合由“可变”变为 "不可变"，这样，这些集合就可以作为字典的键值。

首先来测试一下上面代码，看看运行效果：

if __name__ == '__main__':
    # 导入数据集
    myDat = loadDataSet()
    # 构建第一个候选项集列表C1
    C1 = createC1( myDat )

    # 构建集合表示的数据集 D
    D = map( set, myDat )
    # 选择出支持度不小于0.5 的项集作为频繁项集
    L, suppData = scanD( D, C1, 0.5 )

    print u"频繁项集L：", L
    print u"所有候选项集的支持度信息：", suppData

运行结果：

>>> runfile('E:/Python/PythonScripts/Apriori.py', wdir=r'E:/Python/PythonScripts')
频繁项集L： [frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]
所有候选项集的支持度信息： {frozenset([4]): 0.25, frozenset([5]): 0.75, frozenset([2]): 0.75, frozenset([3]): 0.75, frozenset([1]): 0.5}

可以看出，只有支持度不小于 0.5 的项集被选中到 L 中作为频繁项集，根据不同的需求，我们可以设定最小支持度的值，从而得到我们想要的频繁项集。

　　上面的示例只是选择出来了项集中只包含一个元素的频繁项集，下面需要整合上面的代码，选择出包含 2个，3个直至个数据等于所有候选元素个数的频繁项集，

从而形成完整的 $Apriori$ 的算法，首先给出伪代码：

当集合中的元素个数大于 $0$ 时：

　　构建一个 $k$ 个项组成的候选项集列表

　　检查数据，确认每个项集都是频繁项集

　　保留频繁项集，并构建 $k+1$ 项组成的候选项集的列表

程序清单：

# Aprior算法
def aprioriGen( Lk, k ):
    '''
    由初始候选项集的集合Lk生成新的生成候选项集，
    k表示生成的新项集中所含有的元素个数
    '''
    retList = []
    lenLk = len( Lk )
    for i in range( lenLk ):
        for j in range( i + 1, lenLk ):
            L1 = list( Lk[ i ] )[ : k - 2 ];
            L2 = list( Lk[ j ] )[ : k - 2 ];
            L1.sort();L2.sort()
            if L1 == L2:
                retList.append( Lk[ i ] | Lk[ j ] )
    return retList

def apriori( dataSet, minSupport = 0.5 ):
    # 构建初始候选项集C1
    C1 = createC1( dataSet )

    # 将dataSet集合化，以满足scanD的格式要求
    D = map( set, dataSet )

    # 构建初始的频繁项集，即所有项集只有一个元素
    L1, suppData = scanD( D, C1, minSupport )
    L = [ L1 ]
    # 最初的L1中的每个项集含有一个元素，新生成的
    # 项集应该含有2个元素，所以 k=2
    k = 2

    while ( len( L[ k - 2 ] ) > 0 ):
        Ck = aprioriGen( L[ k - 2 ], k )
        Lk, supK = scanD( D, Ck, minSupport )

        # 将新的项集的支持度数据加入原来的总支持度字典中
        suppData.update( supK )

        # 将符合最小支持度要求的项集加入L
        L.append( Lk )

        # 新生成的项集中的元素个数应不断增加
        k += 1
    # 返回所有满足条件的频繁项集的列表，和所有候选项集的支持度信息
    return L, suppData

关于上面程序 函数 aprioriGen 中的 $k-2$的说明：当利用 {0}, {1}, {2} 这些只含有一个元素的候选项集构建含有 2 个元素的候选项集时，就是两两合并得到 {0,1}, {0,2}, {1,2}; 如果进一步用包含连个元素的候选项集来构建包含 3 个元素的候选项集，同样两两合并，就会得到 {0,1,2},{0,1,2},{0,1,2}. 就是说会出现重复的项集，接下来就需要扫描三元素项集得到非重复结果，显然增加了计算时间。现在，如果比较 {0,1}, {0,2}, {1,2} 的第 0 个元素并只对第 0 个元素相同的集合求并，就会得到 {0,1,2}, 而且只有一次操作，这样就不需要遍历列表来寻找非重复值。

测试上面代码：

if __name__ == '__main__':
    # 导入数据集
    myDat = loadDataSet()
    # 选择频繁项集
    L, suppData = apriori( myDat, 0.5 )
    print u"频繁项集L：", L
    print u"所有候选项集的支持度信息：", suppData

运行结果（最小支持度 0.5） ：

>>> runfile('E:/Python/PythonScripts/Apriori.py', wdir=r'E:/Python/PythonScripts')
频繁项集L： [[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])], [frozenset([2, 3, 5])], []]
所有候选项集的支持度信息： {frozenset([5]): 0.75, frozenset([3]): 0.75, frozenset([2, 3, 5]): 0.5, frozenset([1, 2]): 0.25, frozenset([1, 5]): 0.25, frozenset([3, 5]): 0.5, frozenset([4]): 0.25, frozenset([2, 3]): 0.5, frozenset([2, 5]): 0.75, frozenset([1]): 0.5, frozenset([1, 3]): 0.5, frozenset([2]): 0.75}

在测试一下最小支持度为 0.7 时的情况：

>>> runfile('E:/Python/PythonScripts/Apriori.py', wdir=r'E:/Python/PythonScripts')
频繁项集L： [[frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([2, 5])], []]
所有候选项集的支持度信息： {frozenset([5]): 0.75, frozenset([3]): 0.75, frozenset([3, 5]): 0.5, frozenset([4]): 0.25, frozenset([2, 3]): 0.5, frozenset([2, 5]): 0.75, frozenset([1]): 0.5, frozenset([2]): 0.75}

频繁项集相比最小支持度 0.5 时要少，符合预期。

4.从频繁集中挖掘关联规则 返回目录

　　要找到关联规则，先从一个频繁集开始，我们想知道对于频繁项集中的元素能否获取其它内容，即某个元素或者某个集合可能会推导出另一个元素。从表1 可以得到，如果有一个频繁项集 {豆奶，莴苣}，那么就可能有一条关联规则 "豆奶 --> 莴苣"，意味着如果有人购买了豆奶，那么在统计上他会购买莴苣的概率较大。但是这一条反过来并不一定成立。

　　从一个频繁项集可以产生多少条关联规则呢？可以基于该频繁项集生成一个可能的规则列表，然后测试每条规则的可信度，如果可信度不满足最小值要求，则去掉该规则。类似于前面讨论的频繁项集生成，一个频繁项集可以产生许多可能的关联规则，如果能在计算规则可信度之前就减少规则的数目，就会很好的提高计算效率。

这里有一条规律就是：如果某条规则并不满足最小可信度要求，那么该规则的所有子集也不会满足最小可信度要求，例如下图的解释：

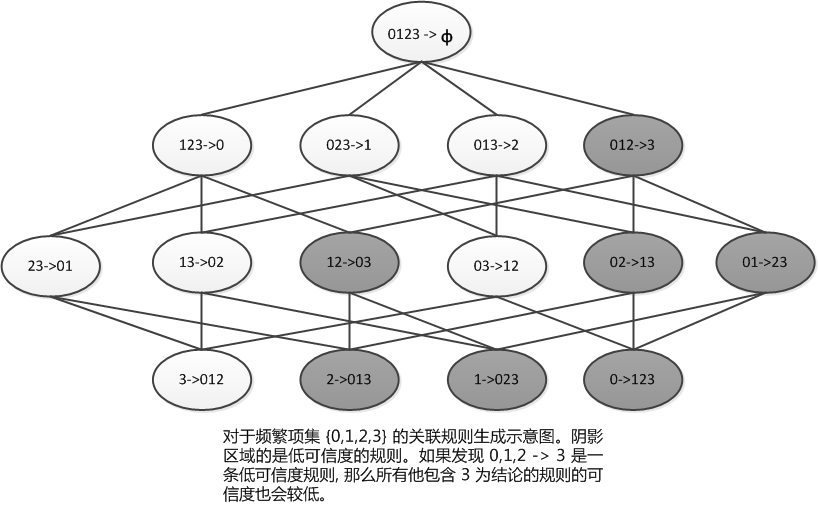
所以，可以利用上图所示的性质来减少测试的规则数目。

关联规则生成函数清单：

# 规则生成与评价
def calcConf( freqSet, H, supportData, brl, minConf=0.7 ):
    '''
    计算规则的可信度，返回满足最小可信度的规则。

    freqSet(frozenset):频繁项集
    H(frozenset):频繁项集中所有的元素
    supportData(dic):频繁项集中所有元素的支持度
    brl(tuple):满足可信度条件的关联规则
    minConf(float):最小可信度
    '''
    prunedH = []
    for conseq in H:
        conf = supportData[ freqSet ] / supportData[ freqSet - conseq ]
        if conf >= minConf:
            print freqSet - conseq, '-->', conseq, 'conf:', conf
            brl.append( ( freqSet - conseq, conseq, conf ) )
            prunedH.append( conseq )
    return prunedH

def rulesFromConseq( freqSet, H, supportData, brl, minConf=0.7 ):
    '''
    对频繁项集中元素超过2的项集进行合并。

    freqSet(frozenset):频繁项集
    H(frozenset):频繁项集中的所有元素，即可以出现在规则右部的元素
    supportData(dict):所有项集的支持度信息
    brl(tuple):生成的规则

    '''
    m = len( H[ 0 ] )

    # 查看频繁项集是否大到移除大小为 m　的子集
    if len( freqSet ) > m + 1:
        Hmp1 = aprioriGen( H, m + 1 )
        Hmp1 = calcConf( freqSet, Hmp1, supportData, brl, minConf )

        # 如果不止一条规则满足要求，进一步递归合并
        if len( Hmp1 ) > 1:
            rulesFromConseq( freqSet, Hmp1, supportData, brl, minConf )

def generateRules( L, supportData, minConf=0.7 ):
    '''
    根据频繁项集和最小可信度生成规则。

    L(list):存储频繁项集
    supportData(dict):存储着所有项集（不仅仅是频繁项集）的支持度
    minConf(float):最小可信度
    '''
    bigRuleList = []
    for i in range( 1, len( L ) ):
        for freqSet in L[ i ]:
            # 对于每一个频繁项集的集合freqSet
            H1 = [ frozenset( [ item ] ) for item in freqSet ]

            # 如果频繁项集中的元素个数大于2，需要进一步合并
            if i > 1:
                rulesFromConseq( freqSet, H1, supportData, bigRuleList, minConf )
            else:
                calcConf( freqSet, H1, supportData, bigRuleList, minConf )
    return bigRuleList

测试：

if __name__ == '__main__':
    # 导入数据集
    myDat = loadDataSet()
    # 选择频繁项集
    L, suppData = apriori( myDat, 0.5 )

    rules = generateRules( L, suppData, minConf=0.7 )
    print 'rules:\n', rules

运行结果：

>>> runfile('E:/Python/PythonScripts/Apriori.py', wdir=r'E:/Python/PythonScripts')
frozenset([1]) --> frozenset([3]) conf: 1.0
frozenset([5]) --> frozenset([2]) conf: 1.0
frozenset([2]) --> frozenset([5]) conf: 1.0
rules:
[(frozenset([1]), frozenset([3]), 1.0), (frozenset([5]), frozenset([2]), 1.0), (frozenset([2]), frozenset([5]), 1.0)]

将可信度降为 0.5 之后：

>>> runfile('E:/Python/PythonScripts/Apriori.py', wdir=r'E:/Python/PythonScripts')
frozenset([3]) --> frozenset([1]) conf: 0.666666666667
frozenset([1]) --> frozenset([3]) conf: 1.0
frozenset([5]) --> frozenset([2]) conf: 1.0
frozenset([2]) --> frozenset([5]) conf: 1.0
frozenset([3]) --> frozenset([2]) conf: 0.666666666667
frozenset([2]) --> frozenset([3]) conf: 0.666666666667
frozenset([5]) --> frozenset([3]) conf: 0.666666666667
frozenset([3]) --> frozenset([5]) conf: 0.666666666667
frozenset([5]) --> frozenset([2, 3]) conf: 0.666666666667
frozenset([3]) --> frozenset([2, 5]) conf: 0.666666666667
frozenset([2]) --> frozenset([3, 5]) conf: 0.666666666667
rules:
[(frozenset([3]), frozenset([1]), 0.6666666666666666), (frozenset([1]), frozenset([3]), 1.0), (frozenset([5]), frozenset([2]), 1.0), (frozenset([2]), frozenset([5]), 1.0), (frozenset([3]), frozenset([2]), 0.6666666666666666), (frozenset([2]), frozenset([3]), 0.6666666666666666), (frozenset([5]), frozenset([3]), 0.6666666666666666), (frozenset([3]), frozenset([5]), 0.6666666666666666), (frozenset([5]), frozenset([2, 3]), 0.6666666666666666), (frozenset([3]), frozenset([2, 5]), 0.6666666666666666), (frozenset([2]), frozenset([3, 5]), 0.6666666666666666)]

一旦降低可信度阈值，就可以获得更多的规则。

5. 总结 返回目录

有上面分析可以看出 Apriori 算法易编码，缺点是在大数据集上可能较慢。