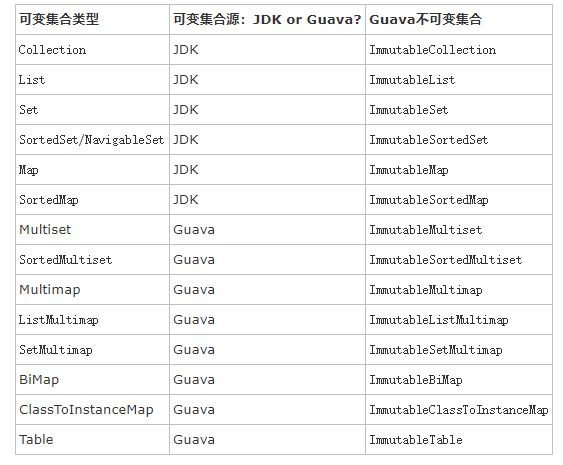
Immutable是为了创建不可变集合使用，不可变集合在很多情况下能提高系统性能。一般使用 .of()或者.builder()<>().put().build()初始化创建不可变集合

Guava Immutable 不可变集合的更多相关文章

  1. java代码之美（4）---guava之Immutable(不可变)集合

    Immutable(不可变)集合 一.概述 guava是google的一个库,弥补了java语言的很多方面的不足,很多在java8中已有实现,暂时不展开.Collections是jdk提供的一个工具类 ...

  2. java代码（4）---guava之Immutable(不可变)集合

    Immutable(不可变)集合   一,概述 guava是google的一个库,弥补了java语音的很多方面的不足,很多在java8中已有实现,暂时不展开,Collections是jdk提供的一个工 ...

  3. Immutable(不可变)集合

    Immutable(不可变)集合 不可变集合,顾名思义就是说集合是不可被修改的.集合的数据项是在创建的时候提供,并且在整个生命周期中都不可改变. 为什么要用immutable对象?immutable对 ...

  4. [Google Guava] 2.1-不可变集合

    范例 01 public static final ImmutableSet<String> COLOR_NAMES = ImmutableSet.of( 02 "red&quo ...

  5. Guava学习笔记：Immutable(不可变)集合

    不可变集合,顾名思义就是说集合是不可被修改的.集合的数据项是在创建的时候提供,并且在整个生命周期中都不可改变. 为什么要用immutable对象?immutable对象有以下的优点: 1.对不可靠的客 ...

  6. Guava集合--Immutable(不可变)集合

    所谓不可变集合,顾名思义就是定义了之后不可修改的集合. 一.为什么要使用不可变集合 不可变对象有很多优点,包括: 当对象被不可信的库调用时,不可变形式是安全的: 不可变对象被多个线程调用时,不存在竞态 ...

  7. Java源码分析:Guava之不可变集合ImmutableMap的源码分析

    一.案例场景 遇到过这样的场景,在定义一个static修饰的Map时,使用了大量的put()方法赋值,就类似这样-- public static final Map<String,String& ...

  8. [Guava官方文档翻译] 7. Guava的Immutable Collection(不可变集合)工具 (Immutable Collections Explained)

    我的技术博客经常被流氓网站恶意爬取转载.请移步原文:http://www.cnblogs.com/hamhog/p/3538666.html ,享受整齐的排版.有效的链接.正确的代码缩进.更好的阅读体 ...

  9. 不可变集合 Immutable Collections

    例子 public static final ImmutableSet<String> COLOR_NAMES = ImmutableSet.of( "red", &q ...

随机推荐

  1. 关于mybatis的@Param注解和参数

    1,使用@Param注解 当以下面的方式进行写SQL语句时: @Select("select column from table where userid = #{userid} " ...

  2. Python调用C++类

    http://blog.csdn.net/liyuan_669/article/details/25361655 C++导出类到Python http://blog.csdn.net/arnozhan ...

  3. python 模块之-configparser

    python 模块configparser   配置文件模块 import configparser    config = configparser.ConfigParser() config[&q ...

  4. NOIP2013题解

    NOIP2013题解 Day1 转圈游戏 circle 快速幂模板题. #include<iostream> using namespace std; int n,m,k,x; int f ...

  5. poj3114 Contries in War (tarjan+dijkstra)

    缩完点后对每次询问做dijkstra即可 #include<cstdio> #include<cstring> #include<algorithm> #inclu ...

  6. RocketMQ介绍与云服务器安装

    RocketMQ 介绍与概念 在github上的说法来看: Apache RocketMQ是一个分布式消息传递和流媒体平台,具有低延迟,高性能和可靠性,万亿级容量和灵活的可扩展性.它提供了多种功能: ...

  7. Spring Cloud(三) --- hystrix

    Hystrix 说到Hystrix就得先说一下产生的背景等等,那就是雪崩效应. 在微服务中肯定存在多个服务层之间的调用,基础服务的故障可能会导致级联故障,进而造成整个系统不可用的情况,这种现象被称为服 ...

  8. [POI2015]CZA

    [POI2015]CZA p很小,讨论 p=0... p=1... p=2:n-1放左或者放右两种情况,剩下怎么放是固定的,模拟然后判断即可 p=3: 正着做要状压,类似放书和排座位那些题,考虑以某个 ...

  9. dij与prim算法

    两种算法本质是相同的. 都是从某一个点开始进行延伸,不断更新一个dis值,直到所有的点都被遍历到,从而求出一个最短路或者是一个树的边权的最小总和. 朴素算法都是n^2,都可以采用堆优化处理,降低复杂度 ...

  10. std::lock_guard和std::unique_lock

    std::unique_lock也可以提供自动加锁.解锁功能,比std::lock_guard更加灵活 https://www.cnblogs.com/xudong-bupt/p/9194394.ht ...