LR(0)文法项目集规范族、DFA和分析表的构建实例
最近在复习编译原理,考试之前以为自己懂了,眼高手低就没去实践。结果一考试出问题了。。。。
一、概念
1.概念解释
2.例子
二、实现步骤
1.扩展文法
2.求出项目集规范族
3.构造DFA
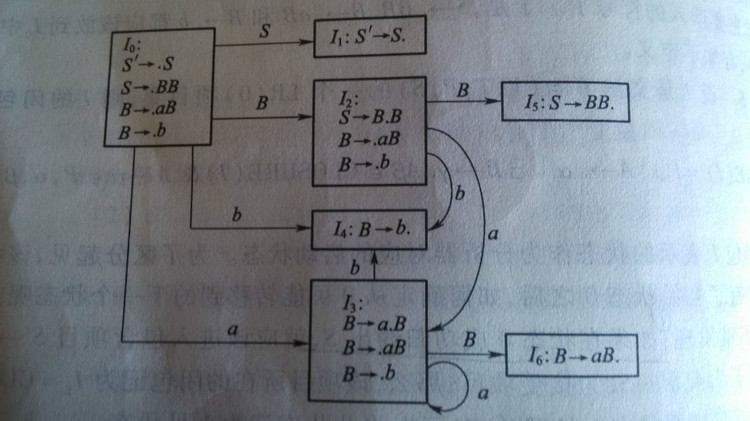
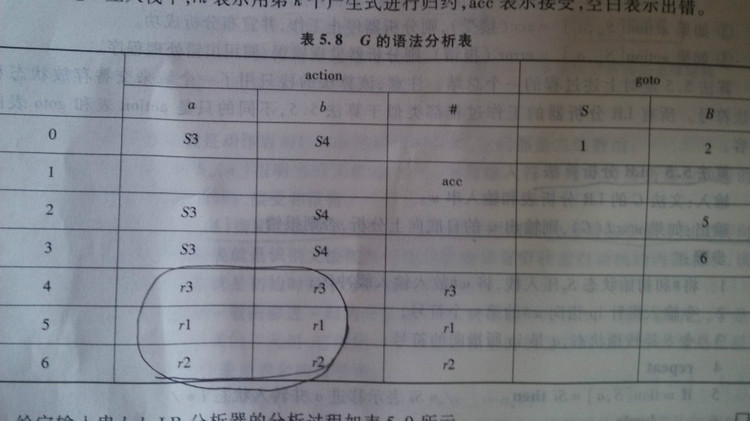
4.构造LR(0)分析表(根据自己画出的DFA图,将分析表填充)
输出:G'的LR(0)分析表(即 Action表和Goto表)
LR(0)文法项目集规范族、DFA和分析表的构建实例的更多相关文章
- 编译原理根据项目集规范族构造LR(0)分析表
转载于https://blog.csdn.net/Johan_Joe_King/article/details/79058597?utm_medium=distribute.pc_relevant.n ...
- 编译原理LR(0)项目集规范族的构造详解
转载于https://blog.csdn.net/johan_joe_king/article/details/79051993#comments 学编译原理的时候,感觉什么LL(1).LR(0).S ...
- 求LR(0)文法的规范族集和ACTION表、GOTO表的构造算法
原理 数据结构 // GO private static Map<Map<Integer,String>,Integer> GO = new HashMap<Map< ...
- vue-cli3.0 Typescript 项目集成环信WebIM 群组聊天
项目背景 环信webim 官方没有vue版本的,自己就根据sdk重写了个vue版本的,只实现了基础的 登录 群组功能,其他的可以根据需要参考官方文档,添加相应的功能. 环信webim SDK相关文档: ...
- 《编译原理》LR 分析法与构造 LR(1) 分析表的步骤 - 例题解析
<编译原理>LR 分析法与构造 LR(1) 分析表的步骤 - 例题解析 笔记 直接做题是有一些特定步骤,有技巧.但也必须先了解一些基本概念,本篇会通过例题形式解释概念,会容易理解和记忆,以 ...
- LL(1),LR(0),SLR(1),LR(1),LALR(1)的 联系与区别
一:LR(0),SLR(1),规范LR(1),LALR(1)的关系 首先LL(1)分析法是自上而下的分析法.LR(0),LR(1),SLR(1),LALR(1)是自下而上的分析法. ...
- LL(1),LR(0),SLR(1),LALR(1),LR(1)对比与分析
前言:考虑到这几种文法如果把具体内容讲下来肯定篇幅太长,而且繁多的符号对初学者肯定是极不友好的,而且我相信看这篇博客的人已经对这几个文法已经有所了解了,本篇博客的内容只是对 这几个文法做一下对比,加深 ...
- C# 语法分析器(二)LR(0) 语法分析
系列导航 (一)语法分析介绍 (二)LR(0) 语法分析 (三)LALR 语法分析 (四)二义性文法 (五)错误恢复 (六)构造语法分析器 首先,需要介绍下 LALR 语法分析的基础:LR(0) 语法 ...
- LR(1)文法分析器 //c++ 实现
1.先读入终结符,非终结符,和所有产生式. 2.预处理:初始化:getpp()获得每个非终结符在产生式左边时的产生式编号, 记录在 string getp[]中(可以多个). 3.获得所有的符号的fi ...
随机推荐
- oracle 18c centos7 设置开机自动启动Oracle
学习自: http://blog.csdn.net/condywl/article/details/57129696 1. 在root用户下进行修改 配置文件 /etc/oratab vim /etc ...
- Jquery ajax 数据更新
$(function(){ var $personWifePs=$("#wife-money tbody tr"); var $personWife=$("#wife-m ...
- Fantacy团队周一站立会议
词频分析模型 1.首先这次站会是周一开的,但是由于我个人的疏忽,没有落实到博客上,请见谅,连累了组长. 2.会议时间:2016年3月28日12:00~12:30. 持续时长:30分钟 会议参加成员:组 ...
- python代码格式检查工具部署pre_commit
如何使用pre_commit?1. 合并该分支 2. 在git根目录下使用pre-commit install即可3. 如果没有装pre-commit 安装一下pip install pre-comm ...
- Bootstrap滚动监控器
前面的话 滚动监听插件是用来根据滚动条所处的位置来自动更新导航项的.滚动导航条下面的区域并关注导航项的变化,下拉菜单中的条目也会自动高亮显示.本文将详细介绍Bootstrap滚动监控器 基本用法 滚动 ...
- codeforces 1051 D. Bicolorings (DP)
D. Bicolorings time limit per test 2 seconds memory limit per test 256 megabytes input standard inpu ...
- maven 父工程 消除重复 对子模块进行管理 主要继承依赖
子类继承父类的 可以不需要groupid与versionid
- 闭包自由变量引用对象的问题 http://bbs.pythontab.com/thread-4266-1-1.html
- BZOJ3963 WF2011MachineWorks(动态规划+斜率优化+cdq分治)
按卖出时间排序后,设f[i]为买下第i台机器后的当前最大收益,则显然有f[i]=max{f[j]+gj*(di-dj-1)+rj-pi},且若此值<0,应设为-inf以表示无法购买第i台机器. ...
- Dapper 连表查询
实体类: UserInfo: public partial class UserInfo { public UserInfo() { this.Persion = new HashSet<Per ...
