[bzoj5507] [洛谷P5305] [gzoi2019]旧词

Descriptioin

浮生有梦三千场

穷尽千里诗酒荒

徒把理想倾倒

不如早还乡

温一壶风尘的酒

独饮往事迢迢

举杯轻思量

泪如潮青丝留他方

——乌糟兽/愚青《旧词》

你已经解决了五个问题，不妨在这大树之下，吟唱旧词一首抒怀。最后的问题就是关于这棵树的，它的描述很简单。

给定一棵 \(n\) 个点的有根树，节点标号 \(1 \sim n\)，11 号节点为根。

给定常数 \(k\) 。

给定 \(Q\) 个询问，每次询问给定 \(x,y\)。

求：

\(\sum\limits_{i\leq x} depth(lca(i,y))^k\)

\(lca(x,y)\) 表示节点 \(x\) 与节点 \(y\) 在有根树上的最近公共祖先。

\(depth(x)\) 表示节点 \(x\) 的深度，根节点的深度为 1。

由于答案可能很大，你只需要输出答案模 998244353 的结果。

Input

输入包含 \(n+Q\) 行。

第 1 行，三个正整数 \(n,Q,k\) 。

第 \(i=2 \sim n\) 行，每行有一个正整数 \(f_i,(1 \leq f_i \leq n)\)，表示编号为 \(i\) 的节点的父亲节点的编号。

接下来 $ Q$ 行，每行两个正整数 \(x,y(1 \leq x,y \leq n)\)，表示一次询问。

Output

输出包含 \(Q\) 行，每行一个整数，表示答案模 998244353 的结果。

Sample Input

5 5 2

1

4

1

2

4 3

5 4

2 5

1 2

3 2

Sample Output

15

11

5

1

6

HINT

样例解释

输入的树：

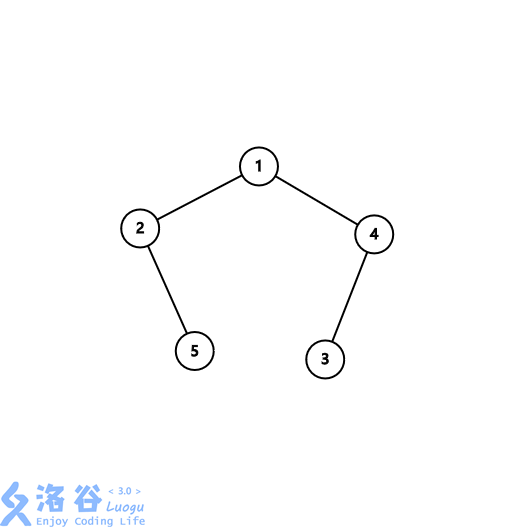
每个点的深度分别为 1,2,3,2,3。

第一个询问 \(x = 4,y = 3\)，容易求出：

\(lca(1,3)=1,lca(2,3)=1,lca(3,3)=3,lca(4,3)=4\)

于是 \(depth(1) +depth(1) +depth(3) +depth(4) =1+1+9+4=15\) 。

数据范围 \(n\leq 50000,m\leq 50000,1\leq k \leq 10^9\)

---

想法

首先一句题外话，我真的很喜欢这种有些文学范儿的题~

言归正传！这个题跟 \([LNOI2014]LCA\) 很像，挺套路的。

离线，把所有询问按 \(x\) 从小到大排序后处理。

考虑当 \(k=1\) 时，将 \(1\leadsto [1,x]\) 每条路径上经过的点的值都加1，统计 \(1\leadsto y\) 路径上所有点的值之和就是答案

这样做的原理为 对于任意深度为 \(i\) 的点，它对答案的贡献为 $ i^1-(i-1)1=1 $

那么当 \(k \neq 1\) 时也同理，任意深度为 \(i\) 的点对答案的贡献为 \(i^k-(i-1)^k=c\) ，路径上若经过这个点，则该点的值加 \(c\)

由于所有点深度固定，\(k\) 也固定， \(c\) 是很容易处理出来的。

至于如何修改与统计，那当然是树链剖分+线段树咯！（虽说 \(lct\) 也行,但想想那代码量与极大的常数还是放弃吧 ）

---

代码

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

int read(){
    int x=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) x=x*10+ch-'0',ch=getchar();
    return x;
}

const int N = 50005;
const int xzy = 998244353;
typedef long long ll;

struct node{
    int v;
    node *nxt;
}pool[N],*h[N];
int cnt;
void addedge(int u,int v){
    node *p=&pool[++cnt];
    p->v=v;p->nxt=h[u];h[u]=p;
}

int fa[N],son[N],dep[N],size[N];
void dfs1(int u){
    int v,sonnum=0;
    size[u]=1;
    for(node *p=h[u];p;p=p->nxt){
        dep[v=p->v]=dep[u]+1;
        dfs1(v);
        if(size[v]>sonnum) sonnum=size[v],son[u]=v;
        size[u]+=size[v];
    }
}
int top[N],w[N],rk[N],tot;
void dfs2(int u){
    int v=son[u];
    if(v){
        top[v]=top[u];
        w[v]=++tot;
        rk[tot]=v;
        dfs2(v);
    }
    for(node *p=h[u];p;p=p->nxt)
        if((v=p->v)!=son[u]){
            top[v]=v;
            w[v]=++tot;
            rk[tot]=v;
            dfs2(v);
        }
}

int n,m,k;
int Pow_mod(int x,int y){
    int ret=1;
    while(y){
        if(y&1) ret=((ll)ret*x)%xzy;
        x=((ll)x*x)%xzy;
        y>>=1;
    }
    return ret;
}

struct tree{
    tree *ch[2];
    int e,sum,lazy;
}pool2[N*2],*root;
int cnt2;
void build(tree *p,int l,int r){
    p->sum=p->lazy=0;
    if(l==r){
        p->e=(Pow_mod(dep[rk[l]],k)-Pow_mod(dep[rk[l]]-1,k)+xzy)%xzy;
        return;
    }
    int mid=(l+r)>>1;
    build(p->ch[0]=&pool2[++cnt2],l,mid);
    build(p->ch[1]=&pool2[++cnt2],mid+1,r);
    p->e=((ll)p->ch[0]->e+p->ch[1]->e)%xzy;
}
void update(tree *p) { p->sum=((ll)p->ch[0]->sum+p->ch[1]->sum)%xzy; }
void pushdown(tree *p){
    if(!p->lazy) return;
    for(int i=0;i<2;i++){
        (p->ch[i]->lazy+=p->lazy)%=xzy;
        p->ch[i]->sum=((ll)p->ch[i]->sum+1ll*p->lazy*p->ch[i]->e%xzy)%xzy;
    }
    p->lazy=0;
}
void change(tree *p,int l,int r,int L,int R){
    if(l==L && r==R){
        p->lazy++;
        p->sum=(p->sum+p->e)%xzy;
        return;
    }
    pushdown(p);
    int mid=(l+r)>>1;
    if(R<=mid) change(p->ch[0],l,mid,L,R);
    else if(L>mid) change(p->ch[1],mid+1,r,L,R);
    else{
        change(p->ch[0],l,mid,L,mid);
        change(p->ch[1],mid+1,r,mid+1,R);
    }
    update(p);
}
int query(tree *p,int l,int r,int L,int R){
    if(l==L && r==R) return p->sum;
    pushdown(p);
    int mid=(l+r)>>1;
    if(R<=mid) return query(p->ch[0],l,mid,L,R);
    else if(L>mid) return query(p->ch[1],mid+1,r,L,R);
    return (query(p->ch[0],l,mid,L,mid)+query(p->ch[1],mid+1,r,mid+1,R))%xzy;
}

void add(int x){
    while(x){
        change(root,1,n,w[top[x]],w[x]);
        x=fa[top[x]];
    }
}
int ask(int x){
    int ret=0;
    while(x){
        (ret+=query(root,1,n,w[top[x]],w[x]))%=xzy;
        x=fa[top[x]];
    }
    return ret;
}

struct data{
    int x,y,id;
    bool operator < (const data &b) const{ return x<b.x; }
}d[N];
int ans[N];

int main()
{
    n=read(); m=read(); k=read();
    for(int i=2;i<=n;i++) {
        fa[i]=read();
        addedge(fa[i],i);
    }
    for(int i=0;i<m;i++) {
        d[i].x=read(); d[i].y=read();
        d[i].id=i;
    }
    sort(d,d+m);

    dep[1]=1;
    dfs1(1);
    top[1]=1; w[1]=++tot; rk[tot]=1;
    dfs2(1);
    build(root=&pool2[++cnt2],1,n);

    int t=0;
    for(int i=0;i<m;i++){
        while(t<d[i].x) add(++t);
        ans[d[i].id]=ask(d[i].y);
    }
    for(int i=0;i<m;i++) printf("%d\n",ans[i]);

    return 0;
}