leetcode-11-盛水最多的容器

题目描述：

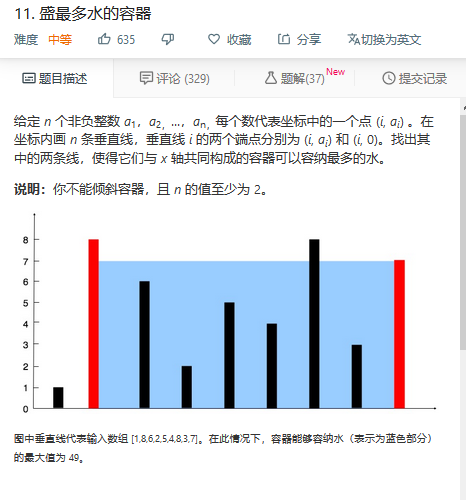
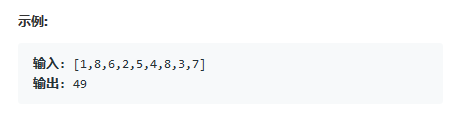
方法一：双指针

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height)-1
        area = 0
        while left<right:
            cur = min(height[left],height[right])*(right-left)
            area = max(cur,area)
            if height[left]<height[right]:
                left+=1
            else:
                right-=1
        return area