最近有空用JAVA折腾的一个分类广告源码。

开发放言：JAVA

框架：SpringMVC Hibernate

分布式用重量级EJB 3.0 实现，可以分布JBOSS部署。

前端用 JSP JQUERY

www.roak.com/reg.jsp

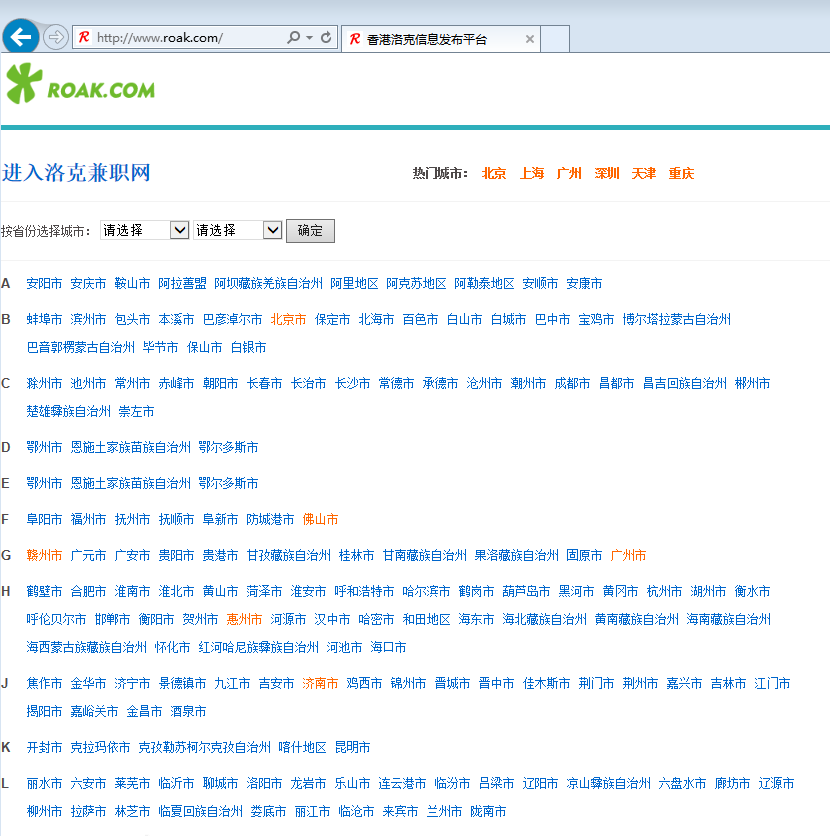
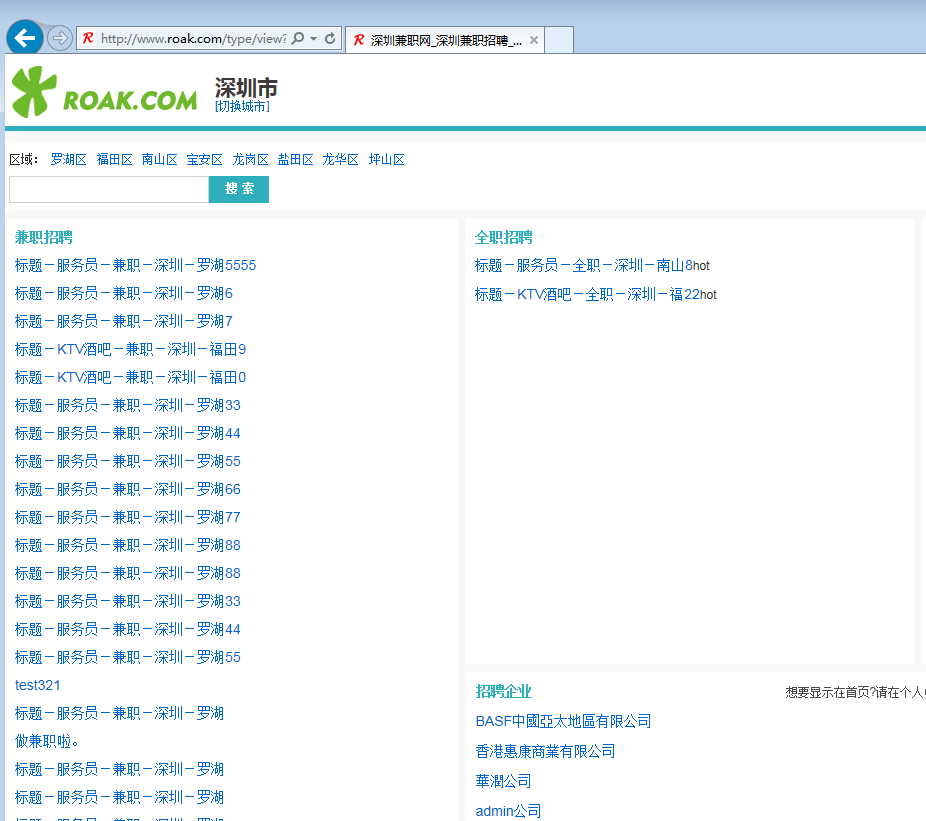
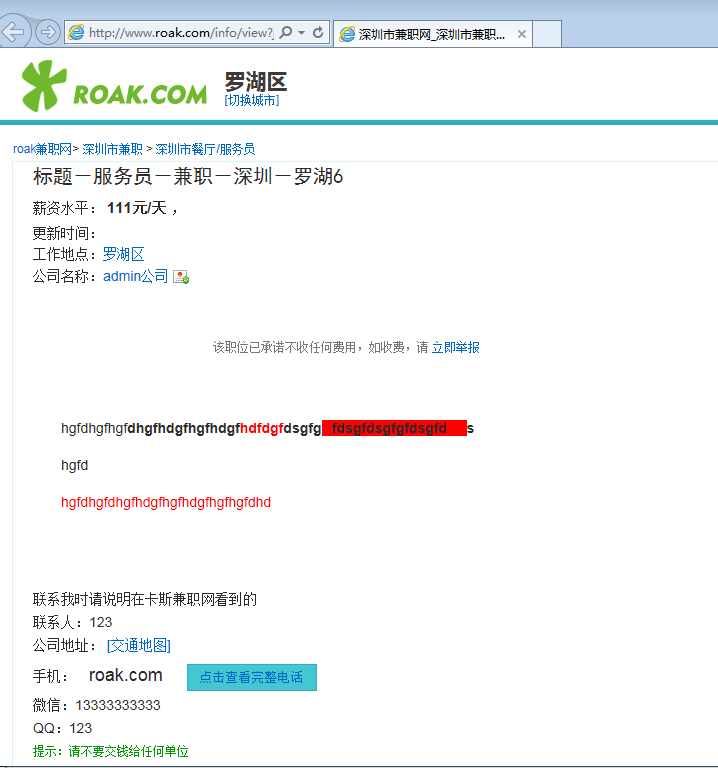
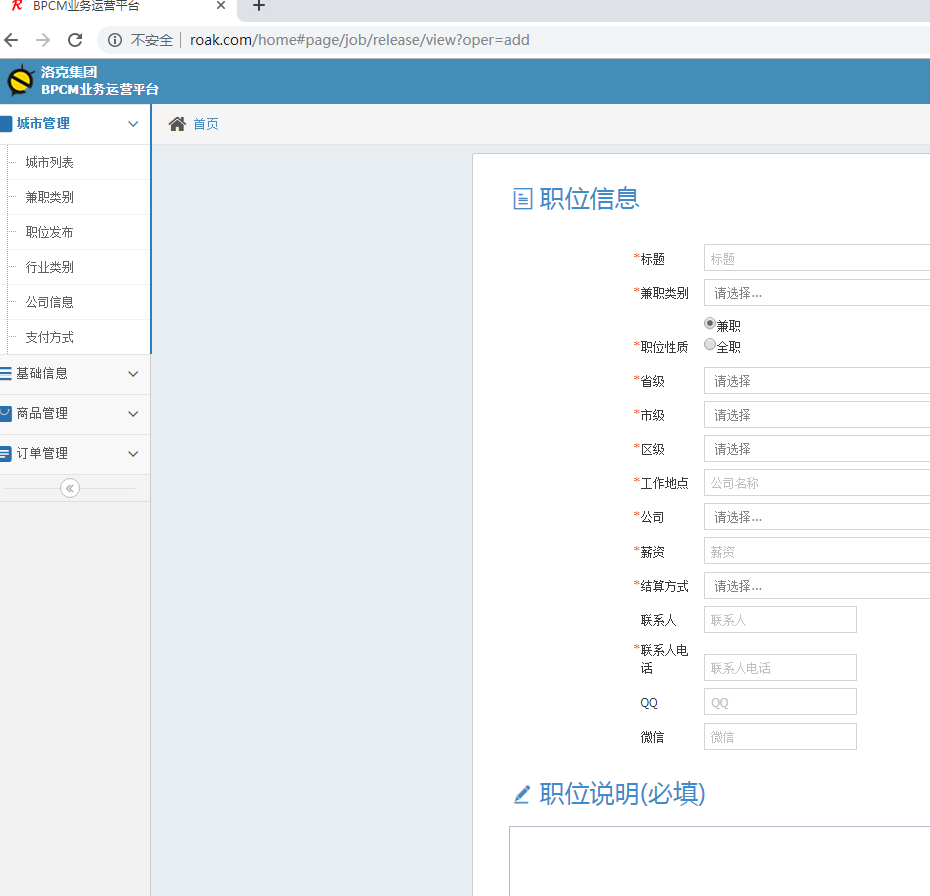
开源一个JAVA开发的分类信息源码的更多相关文章

  1. 开源一个Java Class实现Openfire登陆、推出、消息发送，方便其他系统集成IM功能了

    开源一个Java Class实现Openfire登陆.推出.消息发送 N年前写的,希望对Openfire开发新手有帮助哦 import java.util.*; import java.io.*;   ...

  2. java程序保护如何知识产权，特别提供一个java 开发的java 源代码级的混淆器

    java程序保护如何知识产权,特别提供一个java 开发的java 源代码级的混淆器 下载地址:http://yunpan.cn/QXhEcGNYLgwTD 运行方式:java -jar Encryp ...

  3. 混淆器：java程序保护如何知识产权，特别提供一个java 开发的java 源代码级的混淆器

    java程序保护如何知识产权,特别提供一个java 开发的java 源代码级的混淆器 下载地址:http://yunpan.cn/QXhEcGNYLgwTD 运行方式:java -jar Encryp ...

  4. 作为一个Java开发你用过Jib吗

    1. 前言 Jib是Google开发的可以直接构建 Java应用的Docker和OCI镜像的类库,以Maven和Gradle插件形式提供.它最骚操作的是可以在没有Docker守护程序的情况下构建,也就 ...

  5. 搭建一个java开发环境的步骤

    首先思考java开发环境需要些什么? 1.适用于我们开发环境的jdk 2.对应开发环境的IDE 3.如果是web应用,还需要web服务器,常用的有Tomcat 1) 下载对应组件 2) 安装 jdk安 ...

  6. 2，搭建一个java开发环境

    (1)java开发需要的条件? 1)适用于环境开发的jdk(里面包括了jre和加热里面包括了jvm) 2)对应开发环境的eclipse 3)如果涉及到web开发,还需要web服务器(Tomcat) ( ...

  7. C#使用Xamarin开发可移植移动应用终章(11.获取设备信息与常用组件,开源一个可开发模版.)

    前言 系列目录 C#使用Xamarin开发可移植移动应用目录 源码地址:https://github.com/l2999019/DemoApp 可以Star一下,随意 - - 说点什么.. 本系列,终 ...

  8. 一个JAVA数据库连接池实现源码

    原文链接:http://www.open-open.com/lib/view/open1410875608164.html // // 一个效果非常不错的JAVA数据库连接池. // from:htt ...

  9. 一个Java开发的Python之路----------------(一)

    最近开始学习Python了,主要是因为现在在给海航通过JAVA写CMDB运维管理平台,我就是作为唯一一个坐在运维屋里的开发,又当爹,又当妈,前端,后台,测试,设计,需求, 发布,统统一把抓!!在Git ...

随机推荐

  1. [JSOI2010]快递服务

    Description Luogu4046 BZOJ1820 Solution 暴力DP很好想,\(f[i][j][k][l]\)表示处理到第\(i\)个任务,三个人在\(i,j,k\)的方案数.显然 ...

  2. vmware运行ubuntu虚拟机出现诡异的鼠标闪烁

    正在开心的写着AC自动机,突然发现鼠标消失了. 习惯性地动动鼠标,却还是没有反应,停止移动鼠标后鼠标却显现了出来??(吃惊.gif 在加载软件的时候,就算鼠标停止也会闪烁(其实这个虚拟机以前加载也会闪 ...

  3. Joining Data with dplyr in R

    目录 inner_join Joining three tables left_join right-join full_join semi- and anti-join Stack Overflow ...

  4. 腾讯短链接url生成接口/腾讯短网址在线生成/新浪微博短链接生成器的分享

    在通常情况下,URL是由系统生成的,通常包括URI路径,多个查询参数,可以对参数进行加密和解密. 当人们要分享某个URL,比如短信,邮件,社交媒体,这就需要短URL.而短网址,顾名思义就是在长度上比较 ...

  5. mysql中循环插入数据

    循环插入1w条数据 表结构: mysql> desc time_table; +-------+-----------+------+-----+-------------------+---- ...

  6. CentOS7利用docker安装MySQL5.7

    CentOS7利用docker安装MySQL5.7 前提条件 centos7 且内核版本高于3.10, 可通过以下命令查看内核版本 uname -r 利用yum 安装docker 安装一些必要的系统工 ...

  7. 关于微信小程序

    1.设置了tabBar的页面,好像用navigator跳不过去.

  8. 第一篇 网站基础知识 第5章 自己动手实现HTTP协议

    第5章 自己动手实现HTTP协议 我们知道HTTP协议是在应用层解析内容的,只需要按照它的报文的格式封装和解析数据就可以了,具体的传输还是使用的Socket,在第4章NioServer的基础上自己做一 ...

  9. C语言注释符号

    同学们认为注释很简单,那我来看看下面的代码是否正确? 1.似是而非的问题 int main() { int/*...*/i; char* s = "abcdefgh //hijklmn&qu ...

  10. Java-POJ1013-Counterfeit Dollar

    在13枚硬币中找出fake的那一个 输入:三次天平称量结果 package poj.ProblemSet; import java.util.Scanner; /* 我怎么觉得是贪心算法呢? 起初对所 ...