JavaScript图形实例：SierPinski三角形

1．SierPinski三角形

Sierpinski三角形是一种分形，由波兰数学家谢尔宾斯基在1915年提出，它是一种典型的自相似集。其生成过程为：

（1）取一个三角形（多数使用等边三角形）；

（2）沿三边中点连线，将它分成四个小三角形；

（3）对上、左、右这三个小三角形重复这一过程。

SierPinski三角形的生成示意如图1所示。

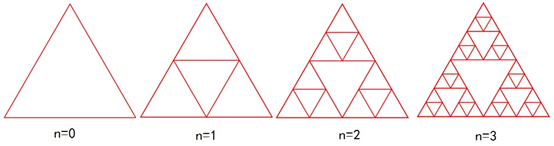
图1 SierPinski三角形的生成

SierPinski三角形采用递归过程易于实现，编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>SierPinski三角形</title>

</head>

<body>

</canvas>

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

var depth =5;

ctx.strokeStyle = "red";

ctx.lineWidth = 3;

function sierpinski(x1,y1,x2,y2,x3,y3,n)

{

if (n<0) return;

ctx.beginPath();

ctx.moveTo(x1,y1);

ctx.lineTo(x2,y2);

ctx.lineTo(x3,y3);

ctx.lineTo(x1,y1);

ctx.closePath();

ctx.stroke();

var x4 = (x1 + x2) / 2;

var y4 = (y1 + y2) / 2;

var x5 = (x2 + x3) / 2;

var y5 = (y2 + y3) / 2;

var x6 = (x1 + x3) / 2;

var y6 = (y1 + y3) / 2;

sierpinski(x1,y1,x4,y4,x6,y6,n-1);

sierpinski(x6,y6,x5,y5,x3,y3,n-1);

sierpinski(x4,y4,x2,y2,x5,y5,n-1);

}

sierpinski(300, 500-500*Math.sqrt(3)/2, 50, 500, 550, 500,depth);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出的SierPinski三角形，如图2所示。

图2 递归深度depth =5的SierPinski三角形

2．SierPinski垫片

SierPinski垫片的生成过程为：

（1）取一个实心的三角形（多数使用等边三角形）；

（2）沿三边中点连线，将它分成四个小三角形，

（3）去掉中间的那一个小三角形；

（4）对其余三个小三角形重复这一过程。

SierPinski垫片的生成示意如图3所示。

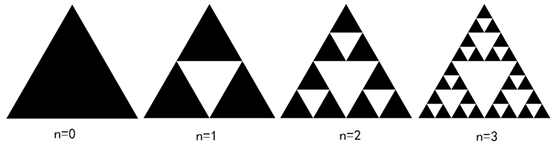
图3 SierPinski垫片的生成

SierPinski垫片采用递归过程易于实现，编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>SierPinski垫片</title>

</head>

<body>

</canvas>

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

ctx.beginPath();

ctx.moveTo(300, 500-500*Math.sqrt(3)/2);

ctx.lineTo(50,500);

ctx.lineTo(550,500);

ctx.closePath();

ctx.fillStyle="black";

ctx.fill();

var depth =5;

ctx.fillStyle = "white";

function sierpinski(x1,y1,x2,y2,x3,y3,n)

{

if (n<=0) return;

var x4 = (x1 + x2) / 2;

var y4 = (y1 + y2) / 2;

var x5 = (x2 + x3) / 2;

var y5 = (y2 + y3) / 2;

var x6 = (x1 + x3) / 2;

var y6 = (y1 + y3) / 2;

ctx.beginPath();

ctx.moveTo(x4,y4);

ctx.lineTo(x5,y5);

ctx.lineTo(x6,y6);

ctx.closePath();

ctx.fill();

sierpinski(x1,y1,x4,y4,x6,y6,n-1);

sierpinski(x6,y6,x5,y5,x3,y3,n-1);

sierpinski(x4,y4,x2,y2,x5,y5,n-1);

}

sierpinski(300, 500-500*Math.sqrt(3)/2, 50, 500, 550, 500,depth);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出的SierPinski垫片，如图4所示。

图4 递归深度depth =5的SierPinski垫片

3．SierPinski地毯

SierPinski垫片的初始图形是三角形，如果将初始图形改成正方形，便可以得到称为SierPinski地毯的图形。它的生成过程为：

（1）取一个实心的正方形；

（2）将正方形的每边三等分，并连接相应的等分点，从而将原正方形等分为面积相等的9个小正方形；

（3）去掉中间的那一个小正方形；

（4）对其余的8个小正方形重复这一过程。

SierPinski垫片的生成示意如图5所示。

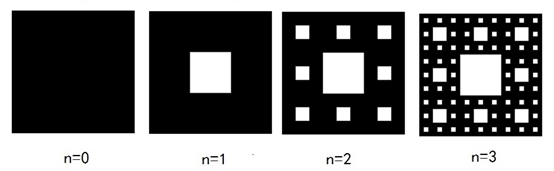
图5 SierPinski地毯的生成

设正方形的左上角坐标为(x,y)，边长为L，则中间正方形的左上角坐标和边长分别为(x+L/3,y+L/3)和L/3，其余8个小正方形的边长均为L/3，左上角坐标分别为(x,y)、（x+L/3,y）、(x+2*L/3,y)、(x,y+L/3)、(x+2*L/3,y+L/3)、(x,y+2*L/3)、(x+L/3,y+2*L/3)和(x+2*L/3,y+2*L/3)。

为了绘制SierPinski地毯，可以编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>SierPinski地毯</title>

</head>

<body>

</canvas>

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

ctx.fillStyle="black";

ctx.fillRect(50,50,450,450);

var depth =5;

ctx.fillStyle = "white";

function sierpinski(x,y,L,n)

{

if (n<=0) return;

ctx.fillRect(x+L/3,y+L/3,L/3,L/3);

sierpinski(x,y,L/3,n-1);

sierpinski(x+L/3,y,L/3,n-1);

sierpinski(x+2*L/3,y,L/3,n-1);

sierpinski(x,y+L/3,L/3,n-1);

sierpinski(x+2*L/3,y+L/3,L/3,n-1);

sierpinski(x,y+2*L/3,L/3,n-1);

sierpinski(x+L/3,y+2*L/3,L/3,n-1);

sierpinski(x+2*L/3,y+2*L/3,L/3,n-1);

}

sierpinski(50,50,450,depth);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出SierPinski垫片，如图6所示。

图6 递归深度depth =5的SierPinski地毯