给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

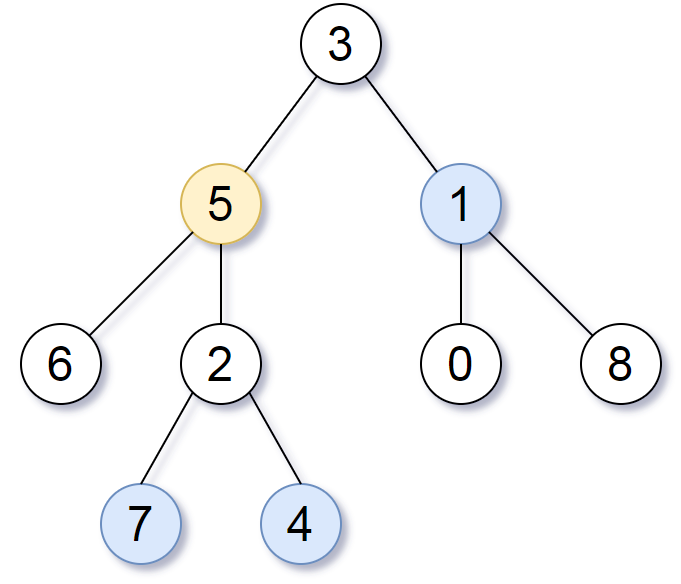
  1. 示例 1：
  3. 输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
  5. 输出：[7,4,1]

解释：

所求结点为与目标结点（值为 5）距离为 2 的结点，

值分别为 7，4，以及 1

注意，输入的 "root" 和 "target" 实际上是树上的结点。

上面的输入仅仅是对这些对象进行了序列化描述。

提示：

给定的树是非空的，且最多有 K 个结点。

树上的每个结点都具有唯一的值 0 <= node.val <= 500 。

目标结点 target 是树上的结点。

0 <= K <= 1000.

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/all-nodes-distance-k-in-binary-tree

一

这道题给了我们一棵二叉树，一个目标结点 target，还有一个整数K，让返回所有跟目标结点 target 相距K的结点。我们知道在子树中寻找距离为K的结点很容易，因为只需要一层一层的向下遍历即可，难点就在于符合题意的结点有可能是祖先结点，或者是在旁边的兄弟子树中，这就比较麻烦了，因为二叉树只有从父结点到子结点的路径，反过来就不行。既然没有，我们就手动创建这样的反向连接即可，这样树的遍历问题就转为了图的遍历（其实树也是一种特殊的图）。建立反向连接就是用一个 HashMap 来来建立每个结点和其父结点之间的映射，使用先序遍历建立好所有的反向连接，然后再开始查找和目标结点距离K的所有结点，这里需要一个 HashSet 来记录所有已经访问过了的结点。

在递归函数中，首先判断当前结点是否已经访问过，是的话直接返回，否则就加入到 visited 中。再判断此时K是否为0，是的话说明当前结点已经是距离目标结点为K的点了，将其加入结果 res 中，然后直接返回。否则分别对当前结点的左右子结点调用递归函数，注意此时带入 K-1，这两步是对子树进行查找。之前说了，还得对父结点，以及兄弟子树进行查找，这是就体现出建立的反向连接 HashMap 的作用了，若当前结点的父结点存在，我们也要对其父结点调用递归函数，并同样带入 K-1，这样就能正确的找到所有满足题意的点了，参见代码如下：

解法一：

  1. class Solution {
  2. public:
  3.     vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
  4.         if (!root) return {};
  5.         vector<int> res;
  6.         unordered_map<TreeNode*, TreeNode*> parent;
  7.         unordered_set<TreeNode*> visited;
  8.         findParent(root, parent);
  9.         helper(target, K, parent, visited, res);
  10.         return res;
  11.     }
  12.     void findParent(TreeNode* node, unordered_map<TreeNode*, TreeNode*>& parent) {
  13.         if (!node) return;
  14.         if (node->left) parent[node->left] = node;
  15.         if (node->right) parent[node->right] = node;
  16.         findParent(node->left, parent);
  17.         findParent(node->right, parent);
  18.     }
  19.     void helper(TreeNode* node, int K, unordered_map<TreeNode*, TreeNode*>& parent, unordered_set<TreeNode*>& visited, vector<int>& res) {
  20.         if (visited.count(node)) return;
  21.         visited.insert(node);
  22.         if (K == 0) {res.push_back(node->val); return;}
  23.         if (node->left) helper(node->left, K - 1, parent, visited, res);
  24.         if (node->right) helper(node->right, K - 1, parent, visited, res);
  25.         if (parent[node]) helper(parent[node], K - 1, parent, visited, res);
  26.     }
  27. };

既然是图的遍历，那就也可以使用 BFS 来做，为了方便起见，我们直接建立一个邻接链表，即每个结点最多有三个跟其相连的结点，左右子结点和父结点，使用一个 HashMap 来建立每个结点和其相邻的结点数组之间的映射，这样就几乎完全将其当作图来对待了，建立好邻接链表之后，原来的树的结构都不需要用了。既然是 BFS 进行层序遍历，就要使用队列 queue，还要一个 HashSet 来记录访问过的结点。在 while 循环中，若K为0了，说明当前这层的结点都是符合题意的，就把当前队列中所有的结点加入结果 res，并返回即可。否则就进行层序遍历，取出当前层的每个结点，并在邻接链表中找到和其相邻的结点，若没有访问过，就加入 visited 和 queue 中即可。记得每层遍历完成之后，K要自减1，参见代码如下：

解法二：

  1. class Solution {
  2. public:
  3.     vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
  4.         if (!root) return {};
  5.         vector<int> res;
  6.         unordered_map<TreeNode*, vector<TreeNode*>> m;
  7.         queue<TreeNode*> q{{target}};
  8.         unordered_set<TreeNode*> visited{{target}};
  9.         findParent(root, NULL, m);
  10.         while (!q.empty()) {
  11.             if (K == 0) {
  12.                 for (int i = q.size(); i > 0; --i) {
  13.                     res.push_back(q.front()->val); q.pop();
  14.                 }
  15.                 return res;
  16.             }
  17.             for (int i = q.size(); i > 0; --i) {
  18.                 TreeNode *t = q.front(); q.pop();
  19.                 for (TreeNode *node : m[t]) {
  20.                     if (visited.count(node)) continue;
  21.                     visited.insert(node);
  22.                     q.push(node);
  23.                 }
  24.             }
  25.             --K;
  26.         }
  27.         return res;
  28.     }
  29.     void findParent(TreeNode* node, TreeNode* pre, unordered_map<TreeNode*, vector<TreeNode*>>& m) {
  30.         if (!node) return;
  31.         if (m.count(node)) return;
  32.         if (pre) {
  33.             m[node].push_back(pre);
  34.             m[pre].push_back(node);
  35.         }
  36.         findParent(node->left, node, m);
  37.         findParent(node->right, node, m);
  38.     }
  39. };

其实这道题也可以不用 HashMap，不建立邻接链表，直接在递归中完成所有的需求，真正体现了递归的博大精深。在进行递归之前，我们要先判断一个 corner case，那就是当 K==0 时，此时要返回的就是目标结点值本身，可以直接返回。否则就要进行递归了。这里的递归函数跟之前的有所不同，是需要返回值的，这个返回值表示的含义比较复杂，若为0，表示当前结点为空或者当前结点就是距离目标结点为K的点，此时返回值为0，是为了进行剪枝，使得不用对其左右子结点再次进行递归。当目标结点正好是当前结点的时候，递归函数返回值为1，其他的返回值为当前结点离目标结点的距离加1。还需要一个参数 dist，其含义为离目标结点的距离，注意和递归的返回值区别，这里不用加1，且其为0时候不是为了剪枝，而是真不知道离目标结点的距离。

在递归函数中，首先判断若当前结点为空，则直接返回0。然后判断 dist 是否为k，是的话，说目标结点距离当前结点的距离为K，是符合题意的，需要加入结果 res 中，并返回0，注意这里返回0是为了剪枝。否则判断，若当前结点正好就是目标结点，或者已经遍历过了目标结点（表现为 dist 大于0），那么对左右子树分别调用递归函数，并将返回值分别存入 left 和 right 两个变量中。注意此时应带入 dist+1，因为是先序遍历，若目标结点之前被遍历到了，那么说明目标结点肯定不在当前结点的子树中，当前要往子树遍历的话，肯定离目标结点又远了一些，需要加1。若当前结点不是目标结点，也还没见到目标结点时，同样也需要对左右子结点调用递归函数，但此时 dist 不加1，因为不确定目标结点的位置。若 left 或者 right 值等于K，则说明目标结点在子树中，且距离当前结点为K（为啥呢？因为目标结点本身是返回1，所以当左右子结点返回K时，和当前结点距离是K）。接下来判断，若当前结点是目标结点，直接返回1，这个前面解释过了。然后再看 left 和 right 的值是否大于0，若 left 值大于0，说明目标结点在左子树中，我们此时就要对右子结点再调用一次递归，并且 dist 带入 left+1，同理，若 right 值大于0，说明目标结点在右子树中，我们此时就要对左子结点再调用一次递归，并且 dist 带入 right+1。这两步很重要，是之所以能不建立邻接链表的关键所在。若 left 大于0，则返回 left+1，若 right 大于0，则返回 right+1，否则就返回0，参见代码如下：

解法三：

  1. class Solution {
  2. public:
  3.     vector<int> distanceK(TreeNode* root, TreeNode* target, int K) {
  4.         if (K == 0) return {target->val};
  5.         vector<int> res;
  6.         helper(root, target, K, 0, res);
  7.         return res;
  8.     }
  9.     int helper(TreeNode* node, TreeNode* target, int k, int dist, vector<int>& res) {
  10.         if (!node) return 0;
  11.         if (dist == k) {res.push_back(node->val); return 0;}
  12.         int left = 0, right = 0;
  13.         if (node->val == target->val || dist > 0) {
  14.             left = helper(node->left, target, k, dist + 1, res);
  15.             right = helper(node->right, target, k, dist + 1, res);
  16.         } else {
  17.             left = helper(node->left, target, k, dist, res);
  18.             right = helper(node->right, target, k, dist, res);
  19.         }
  20.         if (left == k || right == k) {res.push_back(node->val); return 0;}
  21.         if (node->val == target->val) return 1;
  22.         if (left > 0) helper(node->right, target, k, left + 1, res);
  23.         if (right > 0) helper(node->left, target, k, right + 1, res);
  24.         if (left > 0 || right > 0) return left > 0 ? left + 1 : right + 1;
  25.         return 0;
  26.     }
  27. };

二

方法一： 深度优先搜索

思路

如果节点有指向父节点的引用，也就知道了距离该节点 1 距离的所有节点。之后就可以从 target 节点开始进行深度优先搜索了。

算法

对所有节点添加一个指向父节点的引用，之后做深度优先搜索，找到所有距离 target 节点 K 距离的节点。

  1. class Solution {
  2.     Map<TreeNode, TreeNode> parent;
  3.     public List<Integer> distanceK(TreeNode root, TreeNode target, int K) {
  4.         parent = new HashMap();
  5.         dfs(root, null);
  7.         Queue<TreeNode> queue = new LinkedList();
  8.         queue.add(null);
  9.         queue.add(target);
  11.         Set<TreeNode> seen = new HashSet();
  12.         seen.add(target);
  13.         seen.add(null);
  15.         int dist = 0;
  16.         while (!queue.isEmpty()) {
  17.             TreeNode node = queue.poll();
  18.             if (node == null) {
  19.                 if (dist == K) {
  20.                     List<Integer> ans = new ArrayList();
  21.                     for (TreeNode n: queue)
  22.                         ans.add(n.val);
  23.                     return ans;
  24.                 }
  25.                 queue.offer(null);
  26.                 dist++;
  27.             } else {
  28.                 if (!seen.contains(node.left)) {
  29.                     seen.add(node.left);
  30.                     queue.offer(node.left);
  31.                 }
  32.                 if (!seen.contains(node.right)) {
  33.                     seen.add(node.right);
  34.                     queue.offer(node.right);
  35.                 }
  36.                 TreeNode par = parent.get(node);
  37.                 if (!seen.contains(par)) {
  38.                     seen.add(par);
  39.                     queue.offer(par);
  40.                 }
  41.             }
  42.         }
  44.         return new ArrayList<Integer>();
  45.     }
  47.     public void dfs(TreeNode node, TreeNode par) {
  48.         if (node != null) {
  49.             parent.put(node, par);
  50.             dfs(node.left, node);
  51.             dfs(node.right, node);
  52.         }
  53.     }
  54. }

Python

  1. class Solution(object):
  2.     def distanceK(self, root, target, K):
  3.         def dfs(node, par = None):
  4.             if node:
  5.                 node.par = par
  6.                 dfs(node.left, node)
  7.                 dfs(node.right, node)
  9.         dfs(root)
  11.         queue = collections.deque([(target, 0)])
  12.         seen = {target}
  13.         while queue:
  14.             if queue[0][1] == K:
  15.                 return [node.val for node, d in queue]
  16.             node, d = queue.popleft()
  17.             for nei in (node.left, node.right, node.par):
  18.                 if nei and nei not in seen:
  19.                     seen.add(nei)
  20.                     queue.append((nei, d+1))
  22.         return []

复杂度分析

时间复杂度： O(N)，其中 NN 是树中节点个数。

空间复杂度： O(N)。

方法二： 计算节点之间距离

思路

如果 target 节点在 root 节点的左子树中，且 target 节点深度为 3，那所有 root 节点右子树中深度为 K - 3 的节点到 target 的距离就都是 K。

算法

深度优先遍历所有节点。定义方法 dfs(node)，这个函数会返回 node 到 target 的距离。在 dfs(node) 中处理下面四种情况：

如果 node == target，把子树中距离 target 节点距离为 K 的所有节点加入答案。

如果 target 在 node 左子树中，假设 target 距离 node 的距离为 L+1，找出右子树中距离 target 节点 K - L - 1 距离的所有节点加入答案。

如果 target 在 node 右子树中，跟在左子树中一样的处理方法。

如果 target 不在节点的子树中，不用处理。

实现的算法中，还会用到一个辅助方法 subtree_add(node, dist)，这个方法会将子树中距离节点 node K - dist 距离的节点加入答案。

Java

  1. class Solution {
  2.     List<Integer> ans;
  3.     TreeNode target;
  4.     int K;
  5.     public List<Integer> distanceK(TreeNode root, TreeNode target, int K) {
  6.         ans = new LinkedList();
  7.         this.target = target;
  8.         this.K = K;
  9.         dfs(root);
  10.         return ans;
  11.     }
  13.     // Return vertex distance from node to target if exists, else -1
  14.     // Vertex distance: the number of vertices on the path from node to target
  15.     public int dfs(TreeNode node) {
  16.         if (node == null)
  17.             return -1;
  18.         else if (node == target) {
  19.             subtree_add(node, 0);
  20.             return 1;
  21.         } else {
  22.             int L = dfs(node.left), R = dfs(node.right);
  23.             if (L != -1) {
  24.                 if (L == K) ans.add(node.val);
  25.                 subtree_add(node.right, L + 1);
  26.                 return L + 1;
  27.             } else if (R != -1) {
  28.                 if (R == K) ans.add(node.val);
  29.                 subtree_add(node.left, R + 1);
  30.                 return R + 1;
  31.             } else {
  32.                 return -1;
  33.             }
  34.         }
  35.     }
  37.     // Add all nodes 'K - dist' from the node to answer.
  38.     public void subtree_add(TreeNode node, int dist) {
  39.         if (node == null) return;
  40.         if (dist == K)
  41.             ans.add(node.val);
  42.         else {
  43.             subtree_add(node.left, dist + 1);
  44.             subtree_add(node.right, dist + 1);
  45.         }
  46.     }
  47. }

Python

  1. class Solution(object):
  2.     def distanceK(self, root, target, K):
  3.         ans = []
  5.         # Return distance from node to target if exists, else -1
  6.         # Vertex distance: the # of vertices on the path from node to target
  7.         def dfs(node):
  8.             if not node:
  9.                 return -1
  10.             elif node is target:
  11.                 subtree_add(node, 0)
  12.                 return 1
  13.             else:
  14.                 L, R = dfs(node.left), dfs(node.right)
  15.                 if L != -1:
  16.                     if L == K: ans.append(node.val)
  17.                     subtree_add(node.right, L + 1)
  18.                     return L + 1
  19.                 elif R != -1:
  20.                     if R == K: ans.append(node.val)
  21.                     subtree_add(node.left, R + 1)
  22.                     return R + 1
  23.                 else:
  24.                     return -1
  26.         # Add all nodes 'K - dist' from the node to answer.
  27.         def subtree_add(node, dist):
  28.             if not node:
  29.                 return
  30.             elif dist == K:
  31.                 ans.append(node.val)
  32.             else:
  33.                 subtree_add(node.left, dist + 1)
  34.                 subtree_add(node.right, dist + 1)
  36.         dfs(root)
  37.         return ans

复杂度分析

时间复杂度： O(N)，其中 N 树的大小。

空间复杂度： O(N)。

Leetcode——863.二叉树中所有距离为 K 的结点的更多相关文章

  1. Leetcode 863. 二叉树中所有距离为 K 的结点

    863. 二叉树中所有距离为 K 的结点  显示英文描述 我的提交返回竞赛   用户通过次数39 用户尝试次数59 通过次数39 提交次数174 题目难度Medium 给定一个二叉树(具有根结点 ro ...

  2. 【前缀思想】二叉树中所有距离为 K 的结点

    863. 二叉树中所有距离为 K 的结点 class Solution { Map<TreeNode,String>map=new HashMap<>(); String pa ...

  3. [Swift]LeetCode863. 二叉树中所有距离为 K 的结点 | All Nodes Distance K in Binary Tree

    We are given a binary tree (with root node root), a targetnode, and an integer value K. Return a lis ...

  4. 链表中获取倒数第K个结点

    /* * 链表中查找倒数第K个结点.cpp * * Created on: 2018年5月1日 * Author: soyo */ #include<iostream> using nam ...

  5. 链表习题（8）-寻找单链表中数据域大小为k的结点，并与前一结点交换，如果前一结点存在的情况下

    /*寻找单链表中数据域大小为k的结点,并与前一结点交换,如果前一结点存在的情况下*/ /* 算法思想:定义两个指针,pre指向前驱结点,p指向当前结点,当p->data == k的时候,交换 p ...

  6. LeetCode 230.二叉树中第k小的元素

    题目: 给定一个二叉搜索树,编写一个函数 kthSmallest 来查找其中第 k 个最小的元素. 说明:你可以假设 k 总是有效的,1 ≤ k ≤ 二叉搜索树元素个数. 这道题在leetCode上难 ...

  7. LeetCode 671. 二叉树中第二小的节点(Second Minimum Node In a Binary Tree) 9

    671. 二叉树中第二小的节点 671. Second Minimum Node In a Binary Tree 题目描述 给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 ...

  8. Leetcode Lect4 二叉树中的分治法与遍历法

    在这一章节的学习中,我们将要学习一个数据结构——二叉树(Binary Tree),和基于二叉树上的搜索算法. 在二叉树的搜索中,我们主要使用了分治法(Divide Conquer)来解决大部分的问题. ...

  9. Leetcode 671.二叉树中第二小的节点

    二叉树中第二小的节点 给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0.如果一个节点有两个子节点的话,那么这个节点的值不大于它的子节点的值. 给出这样的一个二叉树 ...

随机推荐

  1. SpringAOP切入点的表达式

    1. 常用的切入点表达式分为:  (1)按类型匹配:within 关键字 (2)按函数匹配:execution (3)按bean的id匹配:bean 2.按类匹配的写法 匹配到具体的类:<aop ...

  2. filebeat+redis+logstash+elasticsearch基本配置--适用于6.4版本

    filebeat配置: filebeat.inputs:- type: log enabled: true paths: - /opt/xxxx.log fields:                ...

  3. SpringBoot基于easyexcel导出和写入Excel

      easyexcel是阿里巴巴旗下开源项目,主要用于Excel文件的导入和导出处理,今天我们利用SpringBoot和easyexcel实战演示如何导出和写入Excel文件. 一.加入我们需要的ea ...

  4. day24(024-多线程(上))

    ###24.01_多线程(多线程的引入)(了解) 1.什么是线程 线程是程序执行的一条路径, 一个进程中可以包含多条线程 多线程并发执行可以提高程序的效率, 可以同时完成多项工作 2.多线程的应用场景 ...

  5. Zookeeper--命令介绍

    参考 https://zookeeper.apache.org/doc/r3.4.13/zookeeperStarted.html#sc_ConnectingToZooKeeper 连接到zookee ...

  6. vsCode--设置显示文件和搜索过滤

    文件位置:文件(File)-首选项(Preference)-设置(setting) 打开setting.json文件输入一下内容即可 { "search.exclude": { & ...

  7. CentOS 7 连接不到网络解决方法

    使用VM12创建虚拟机并安装CentOS 7,但是安装完成后发现连接不到网络. ping jd.com发现不通 因为在创建虚拟机的时候我们选择的是NAT模式 这里给出NAT模式下对应的的解决方法: 一 ...

  8. HDU 3484 Matrix Game 枚举暴力

    上次周赛碰到这个题目,居然都没思路,真是不应该啊,起码也应该想到枚举法. 因为题目只允许每一row进行reverse操作,而每两列可以进行交换操作,所以首先把row的变化固定下来,即枚举第一列与第1- ...

  9. 简单的Vue计算属性

    倒转字符串 <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF ...

  10. maven打包 invalid entry size Failed to execute goal org.springframework.boot:spring-boot-maven-plugin:1.5.14.RELEASE:repackage (default) on project

    打包失败,但是不知是具体是什么引起得,使用mvn -e clean package,定位到报错得代码 在定位到代码,打上断点,使用maven 打包debug模式 找到dubbo.properties, ...