B-树与B+树 两者的区别

一个m阶的B树具有如下几个特征：

• 根结点至少有两个子女。

• 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m

• 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m

• 所有的叶子结点都位于同一层。

• 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

一个m阶的B+树具有如下几个特征：

• 有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。

• 所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

• 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。
  
  
  
  
  
  
  
  
  
  
  
  
  
  

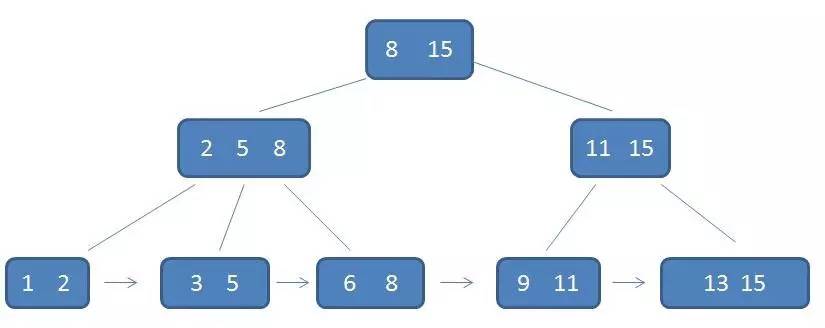
B-树中的卫星数据（Satellite Information）：

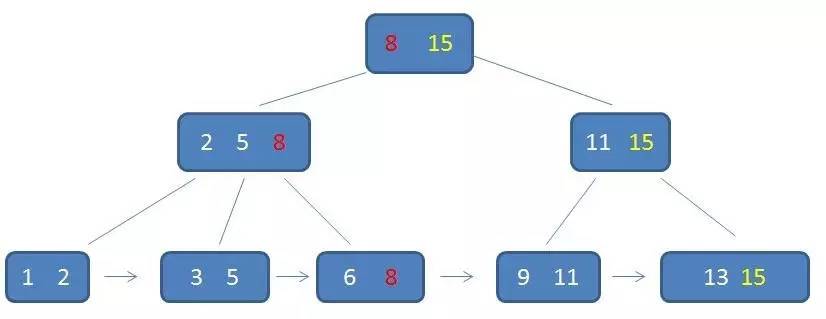
B+树中的卫星数据（Satellite Information）：

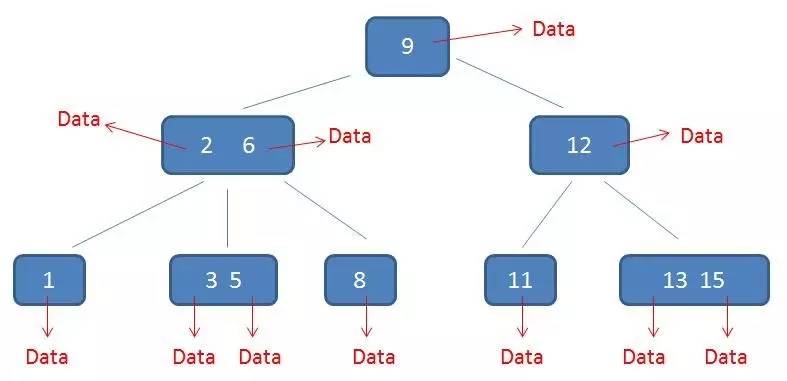
需要补充的是，在数据库的聚集索引（Clustered Index）中，叶子节点直接包含卫星数据。在非聚集索引（NonClustered Index）中，叶子节点带有指向卫星数据的指针。

第一次磁盘IO：

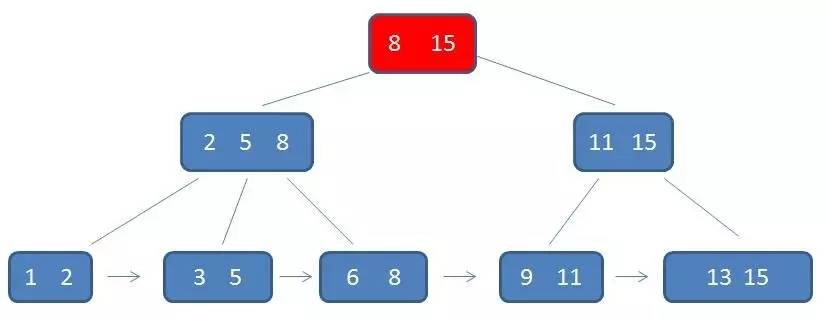
第二次磁盘IO：

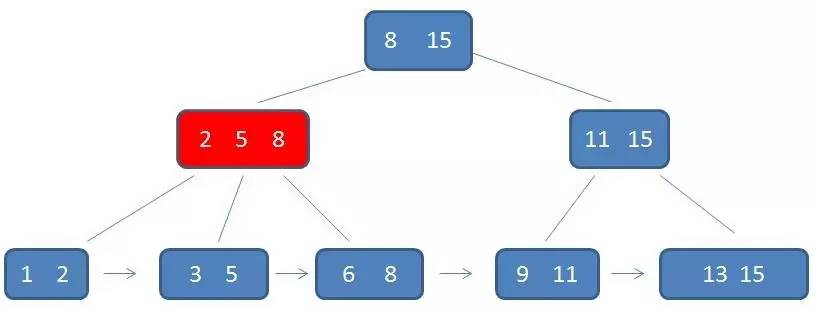
第三次磁盘IO：

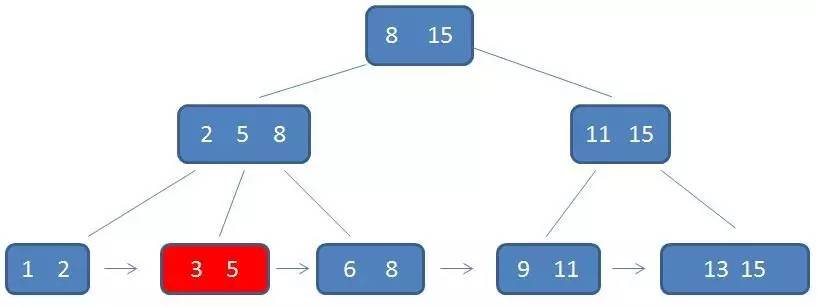
B-树的范围查找过程

自顶向下，查找到范围的下限（3）：

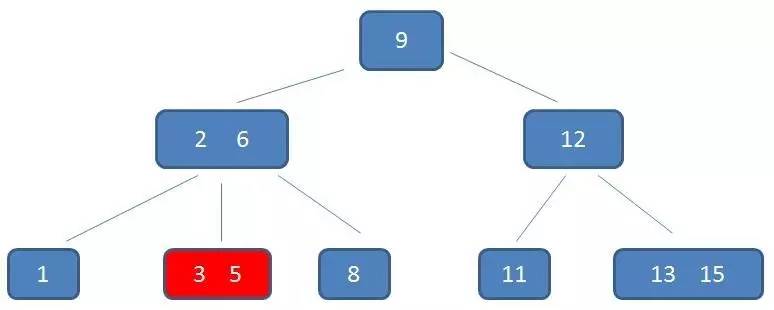
中序遍历到元素6：

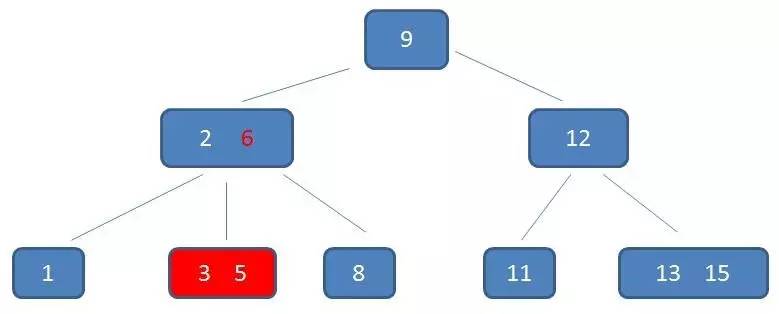
中序遍历到元素8：

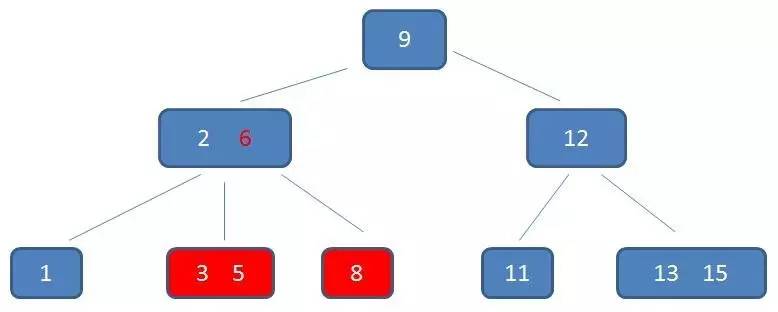
中序遍历到元素9：

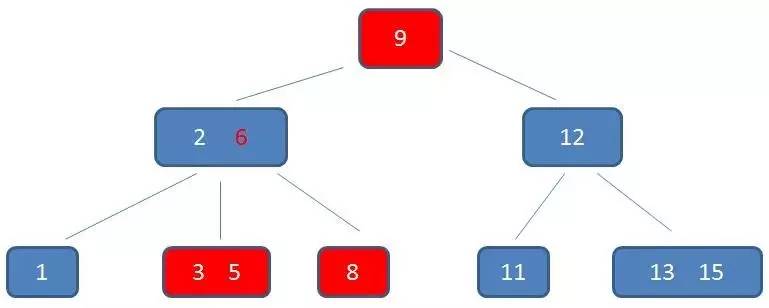
中序遍历到元素11，遍历结束：

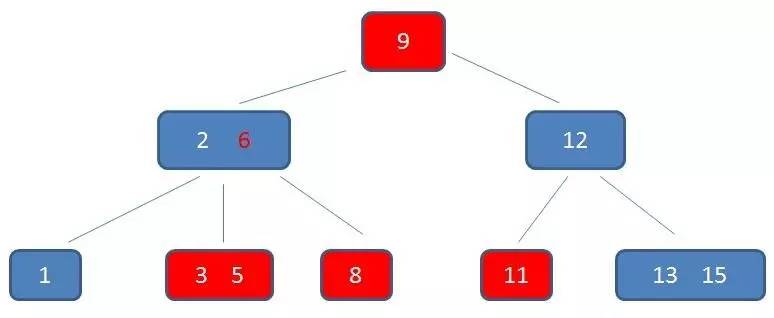
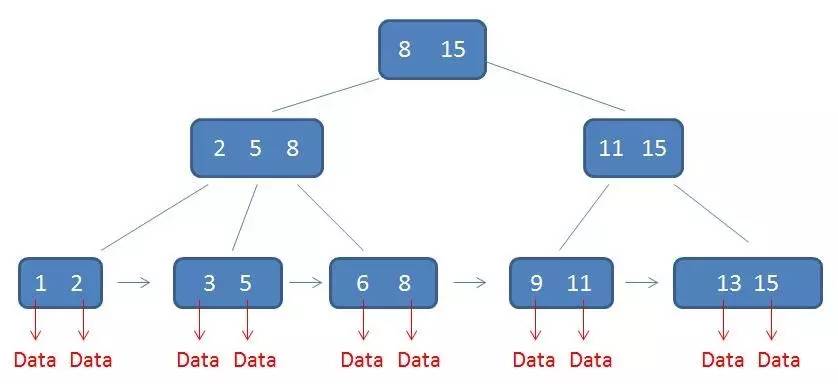
B+树的范围查找过程

自顶向下，查找到范围的下限（3）：

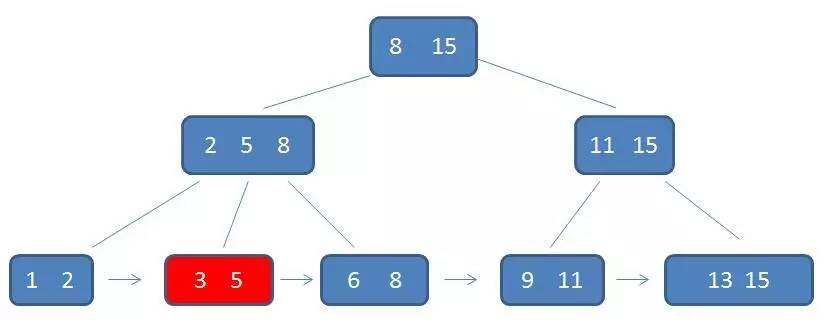
通过链表指针，遍历到元素6, 8：

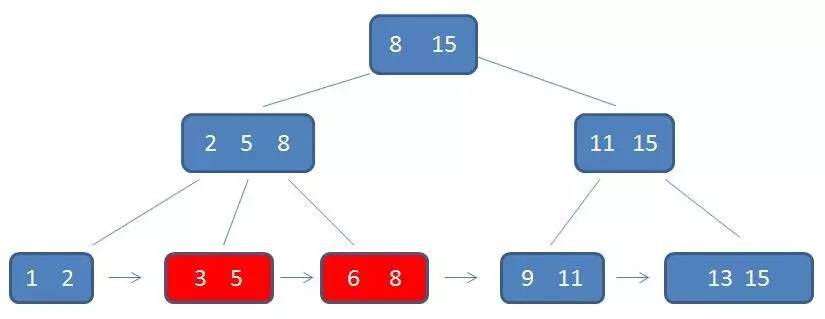
通过链表指针，遍历到元素9, 11，遍历结束：

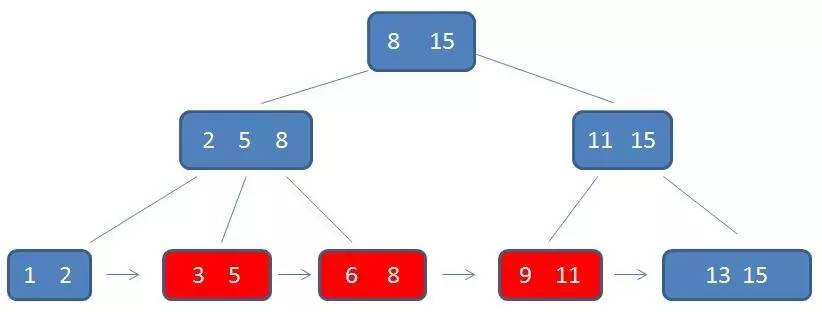
B+树的特征：

• 有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据都保存在叶子节点。

• 所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

• 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

B+树的优势：

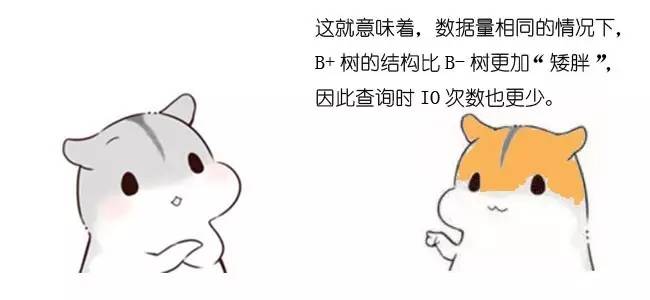
• 单一节点存储更多的元素，使得查询的IO次数更少。

• 所有查询都要查找到叶子节点，查询性能稳定。

• 所有叶子节点形成有序链表，便于范围查询。

转载：https://blog.csdn.net/qq_26222859/article/details/80631121