重复测量的方差分析|Mauchly's Test of Sphericity|

生物统计学-重复测量的方差分析

之前的方差分析应用条件要求组之间是独立的，即某种因素下相同时段测量的结果数据，但4月与5月数据是有关系的，所以必须考虑某种因素下不同时段测量的结果数据，即使用重复测量的方差分析，即处理*基于时间因素的重复测量*同一时间下的重复测量。

这样的好处是克服时间效应，在样本数少的情况下数据量不会太少，但是重复测量使得对象有三种效应。假定测定时间对对象无影响是配对样本t检验的前提，否则用重复测量的方差分析。

使用条件是样本个体之间相互独立，即A患者与B患者没有关系。方差齐性是每种处理方差相同，即所有患者在接受不同处理后的数据，患者A的所有数据与患者B的所有数据的方差都是相同的；协方差球对称性，即通过球对称检验，否则就是有偏的，这需要调自由度。

总变异=个体间（患者在不同处理下的差异）+个体内（患者不同时间点的差异）

1.建立假设2.检验对称性（不同检验方法）

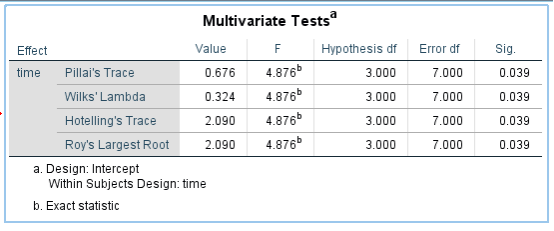
常见是一致的，如果不一致就选择第一个

多重比对必须经过球对称检验：即p-value必须非显著的：

Mauchly's Test of Sphericitya
Measure:   MEASURE_1
Within Subjects Effect	Mauchly's W	Approx. Chi-Square	df	Sig.	Epsilonb
					Greenhouse-Geisser	Huynh-Feldt	Lower-bound
time	0.208	12.131	5	0.034	0.595	0.733	0.333
Tests the null hypothesis that the error covariance matrix of the orthonormalized transformed dependent variables is proportional to an identity matrix.
a. Design: Intercept Within Subjects Design: time
b. May be used to adjust the degrees of freedom for the averaged tests of significance. Corrected tests are displayed in the Tests of Within-Subjects Effects table.

如果该差异是显著的，则不满足球测试，则需要优化此表中的自由度：在组内影响中出现的自由度是经过优化之后的：