python实现逻辑回归

首先得明确逻辑回归与线性回归不同，它是一种分类模型。而且是一种二分类模型。

首先我们需要知道sigmoid函数，其公式表达如下：

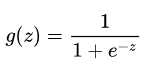
其函数曲线如下：

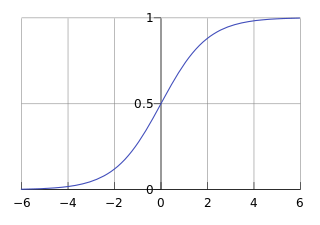
sigmoid函数有什么性质呢？

1、关于（0,0.5） 对称

2、值域范围在(0,1)之间

3、单调递增

4、光滑

5、中间较陡，两侧较平缓

6、其导数为g(z)(1-g(z))，即可以用原函数直接计算

于是逻辑回归的函数形式可以用以下公式表示：

其中θ表示权重参数，x表示输入。θTx为决策边界，就是该决策边界将不同类数据区分开来。

为什么使用sigmoid函数呢？

1、sigmoid函数本身的性质

2、推导而来

我们知道伯努利分布：

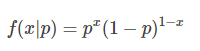
当x=1时，f(1|p) =p，当x=0时，f(0|p)=1-p

首先要明确伯努利分布也是指数族，指数族的一般表达式为：

由于：

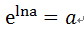
则有：

所以：

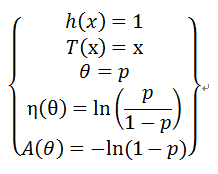
因为：

则有：

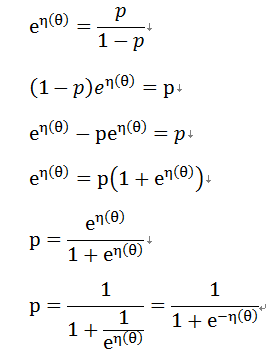
逻辑回归代价函数：

为什么这么定义呢？

以单个样本为例：

上面式子等价于：

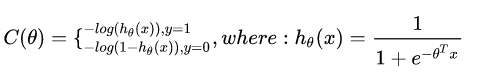
当y=1时，其图像如下：

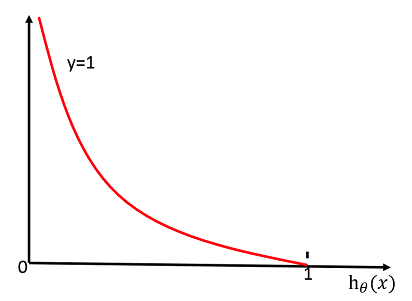
也就是说当hθ(x)的值越接近1，C(θ) 的值就越小。

同理当y=0时，其图像如下：

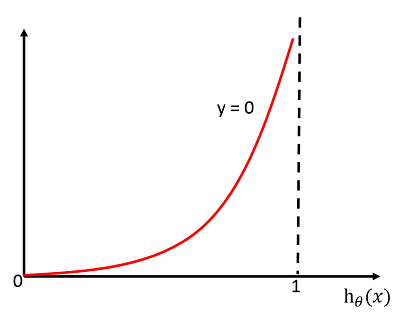
也就是说当hθ(x)的值越接近0，C(θ) 的值就越小。

这样就可以将不同类区分开来。

代价函数的倒数如下：

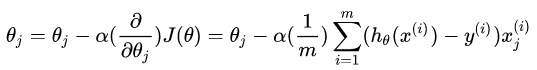
推导过程如下：

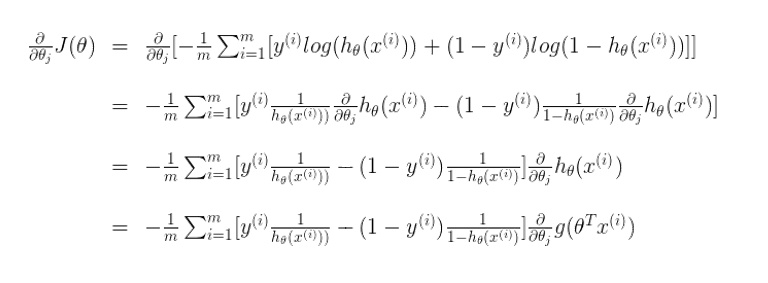
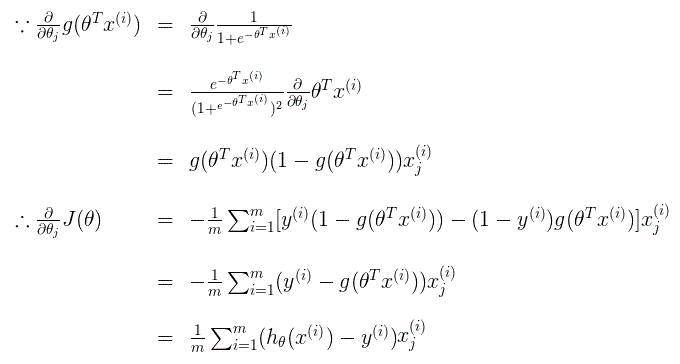
上面参考了：

https://blog.csdn.net/sun_wangdong/article/details/80780368

https://zhuanlan.zhihu.com/p/28415991

接下来就是代码实现了，代码来源： https://github.com/eriklindernoren/ML-From-Scratch

from __future__ import print_function, division
import numpy as np
import math
from mlfromscratch.utils import make_diagonal, Plot
from mlfromscratch.deep_learning.activation_functions import Sigmoid

class LogisticRegression():
    """ Logistic Regression classifier.
    Parameters:
    -----------
    learning_rate: float
        The step length that will be taken when following the negative gradient during
        training.
    gradient_descent: boolean
        True or false depending if gradient descent should be used when training. If
        false then we use batch optimization by least squares.
    """
    def __init__(self, learning_rate=.1, gradient_descent=True):
        self.param = None
        self.learning_rate = learning_rate
        self.gradient_descent = gradient_descent
        self.sigmoid = Sigmoid()

    def _initialize_parameters(self, X):
        n_features = np.shape(X)[1]
        # Initialize parameters between [-1/sqrt(N), 1/sqrt(N)]
        limit = 1 / math.sqrt(n_features)
        self.param = np.random.uniform(-limit, limit, (n_features,))

    def fit(self, X, y, n_iterations=4000):
        self._initialize_parameters(X)
        # Tune parameters for n iterations
        for i in range(n_iterations):
            # Make a new prediction
            y_pred = self.sigmoid(X.dot(self.param))
            if self.gradient_descent:
                # Move against the gradient of the loss function with
                # respect to the parameters to minimize the loss
                self.param -= self.learning_rate * -(y - y_pred).dot(X)
            else:
                # Make a diagonal matrix of the sigmoid gradient column vector
                diag_gradient = make_diagonal(self.sigmoid.gradient(X.dot(self.param)))
                # Batch opt:
                self.param = np.linalg.pinv(X.T.dot(diag_gradient).dot(X)).dot(X.T).dot(diag_gradient.dot(X).dot(self.param) + y - y_pred)

    def predict(self, X):
        y_pred = np.round(self.sigmoid(X.dot(self.param))).astype(int)
        return y_pred

说明：np.linalg.pinv()用于计算矩阵的pseudo-inverse（伪逆）。第一种方法求解使用随机梯度下降。

其中make_diagonal()函数如下：用于将向量转换为对角矩阵

def make_diagonal(x):
    """ Converts a vector into an diagonal matrix """
    m = np.zeros((len(x), len(x)))
    for i in range(len(m[0])):
        m[i, i] = x[i]
    return m

其中Sigmoid代码如下：

class Sigmoid():
    def __call__(self, x):
        return 1 / (1 + np.exp(-x))

    def gradient(self, x):
        return self.__call__(x) * (1 - self.__call__(x))

最后是主函数运行代码：

from __future__ import print_function
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt

# Import helper functions
import sys
sys.path.append("/content/drive/My Drive/learn/ML-From-Scratch/")
from mlfromscratch.utils import make_diagonal, normalize, train_test_split, accuracy_score
from mlfromscratch.deep_learning.activation_functions import Sigmoid
from mlfromscratch.utils import Plot
from mlfromscratch.supervised_learning import LogisticRegression

def main():
    # Load dataset
    data = datasets.load_iris()
    X = normalize(data.data[data.target != 0])
    y = data.target[data.target != 0]
    y[y == 1] = 0
    y[y == 2] = 1

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, seed=1)

    clf = LogisticRegression(gradient_descent=True)
    clf.fit(X_train, y_train)
    y_pred = clf.predict(X_test)

    accuracy = accuracy_score(y_test, y_pred)
    print ("Accuracy:", accuracy)

    # Reduce dimension to two using PCA and plot the results
    Plot().plot_in_2d(X_test, y_pred, title="Logistic Regression", accuracy=accuracy)

if __name__ == "__main__":
    main()

结果：

Accuracy: 0.9393939393939394