luogu P4129 [SHOI2006]仙人掌

题目描述

仙人掌图（cactus）是一种无向连通图，它的每条边最多只能出现在一个简单回路（simple cycle）里面。从直观上说，可以把仙人掌图理解为允许存在回路的树。但是仙人掌图和树之间有个本质的不同，仙人掌图可以拥有多个支撑子图（spanning subgraph），而树的支撑子图只有一个（它自身），我们把仙人掌图的支撑子图的数目称为“仙人数”。你的任务就是计算给定图的“仙人数”。

一些关于仙人掌图的举例：

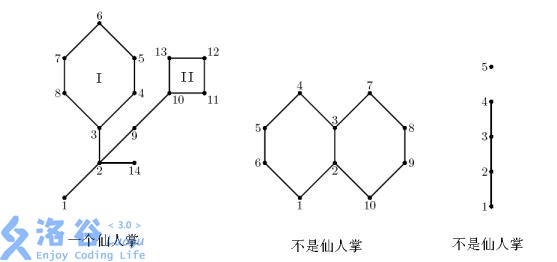
第一张图是一个仙人掌图，第二张图的边（2，3）在两个不同的回路里面，所以不是仙人掌图，第三张图不是一个连通图，所以也不是仙人掌图。

以下是对一些术语的解释：

简单回路（simple cycle）：简单回路是原图的一条路径，这条路径的边集构成了回路，回路中顶点只能出现一次。比如对于上例中第二个图来说，它一共有三个简单回路，分别是（4，3，2，1，6，5）、（7，8，9，10，2，3）和（4，3，7，8，9，10，2，1，6，5）

支撑子图（spanning subgraph）：支撑子图也是原图的子图，这种子图可以比原来少一些边，但是不能破坏图的连通性，也不能去除原来图上的任何顶点。“支撑”的概念类似于我们熟知的“最小支撑树”，对于上例中的第一张图来说，任意去除回路I中的图或回路II中的一条边都能构成一个支撑子图，所以它的支撑子图一共有6 + 4 + 6 × 4 + 1 = 35种（注意图自身也是自己的一个子图）

输入格式

输入文件的第一行是两个整数n和m（1≤n≤20000, 0≤m≤1000）。n代表图的顶点数，顶点的编号总是从1到n表示的。

接下来一共有m行。每行都代表了图上的一条路径（注意：这里所表示的一条路径可不一定是一条回路）。这些行的格式是首先有一个整数ki（2≤ki≤1000）代表这条路径通过了几个顶点，接下来是ki个在1到n之间的数字，其中每个数字代表了图上的一个顶点，相邻的顶点之间就定义了一条边。一条路径上可能通过一个顶点好几次，比如对于第一个例子，第一条路径从2经过3，又从8返回到了3，但是我们保证所有的边都会出现在某条路径上，而且不会重复出现在两条路径上，或者在一条路径上出现两次。

输出格式

输出这张图的“仙人数”，如果它不是一张仙人掌图，输出0。注意最后的答案可能是一个很大很大的数。

输入输出样例

输入 #1复制

14 3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
2 2 14

输出 #1复制

35

输入 #2复制

10 2
7 1 2 3 4 5 6 1
6 3 7 8 9 10 2

输出 #2复制

0

输入 #3复制

5 1
4 1 2 3 4

输出 #3复制

0

思路：注意高精度和与点双不同的是判简单环边数即可

typedef long long LL;
typedef pair<LL, LL> PLL;
const LL bas = ;

struct Big_Number {
    LL a[],len;
    void init() {
        len = ;
        memset(a, , sizeof a);
        a[] = ;
    }
    void mul(LL val) {
        for (int i = ; i < len; i++) {
            a[i] = a[i] * val;
        }
        for (int i = ; i < len; i++){
            a[i + ] += a[i] / bas;
            a[i] %= bas;
        }
        while (a[len]) {
            a[len + ] = a[len] / bas;
            a[len] %= bas;
            len++;
        }
    }
    void print() {
        printf("%lld", a[len - ]);
        for (int i = len - ; i >= ; i--) {
            printf("%.8lld", a[i]);
        }
        printf("\n");
    }
} ans;

const int maxm = 2e6+;
const int maxn = 2e5+;

int head[maxm], edgecnt, dfn[maxn], low[maxn], bcc_cnt, bccnum[maxn], dfs_clock, s[maxm], top, vis[maxn], num;
LL bcc[maxn];
bool ok = true;

struct edge{
    int u, v, nex;
} edges[maxm];

void addedge(int u, int v) {
    edges[++edgecnt].u = u;
    edges[edgecnt].v = v;
    edges[edgecnt].nex = head[u];
    head[u] = edgecnt;
}

void dfs(int u, int fa) {
    vis[u] = ;
    ++num;
    for(int i = head[u]; i; i = edges[i].nex) {
        int v = edges[i].v;
        if(v == fa) continue;
        if(!vis[v])
            dfs(v, u);
    }
}

void tarjan(int u, int fa) {
    dfn[u] = low[u] = ++dfs_clock;
    int child = , v;
    for(int i = head[u]; i; i = edges[i].nex) {
        v = edges[i].v;
        if(v == fa) continue;
        if(!dfn[v]) {
            s[++top] = i;
            tarjan(v, u);
            low[u] = min(low[u], low[v]);
            if(low[v] >= dfn[u]) {
                ++bcc_cnt;
                LL vet = ;
                while(true) {
                    int num = s[top--];
                    if(bccnum[edges[num].v] != bcc_cnt) {
                        vet++;
                        bccnum[edges[num].v]=bcc_cnt;
                    } else ok = false;
                    if(edges[num].u == u && edges[num].v == v) break;
                }
                if(ok && vet>)
                    ans.mul(vet+);
            }
        } else if(dfn[v] < dfn[u]){
            s[++top] = i;
            low[u] = min(low[u], dfn[v]);
        }
    }
}

void run_case() {
    int n, m, u, v, t;
    ans.init();
    cin >> n >> m;
    for(int i = ; i <= m; ++i) {
        cin >> t;
        t--;
        cin >> u;
        while(t--) {
            cin >> v;
            addedge(u, v), addedge(v, u);
            u = v;
        }
    }
    dfs(n, -);
    if(n != num) {
        cout << "";
        return;
    }
    tarjan(, -);
    if(!ok) cout << "";
    else
        ans.print();
}

int main() {
    //ios::sync_with_stdio(false), cin.tie(0);
    run_case();
    return ;
}

(自用板，记录每一个点双和割点