[模拟] Codeforces - 1191C - Tokitsukaze and Discard Items

Tokitsukaze and Discard Items

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Recently, Tokitsukaze found an interesting game. Tokitsukaze had nn items at the beginning of this game. However, she thought there were too many items, so now she wants to discard mm (1≤m≤n1≤m≤n) special items of them.

These nn items are marked with indices from 11 to nn. In the beginning, the item with index ii is placed on the ii-th position. Items are divided into several pages orderly, such that each page contains exactly kk positions and the last positions on the last page may be left empty.

Tokitsukaze would do the following operation: focus on the first special page that contains at least one special item, and at one time, Tokitsukaze would discard all special items on this page. After an item is discarded or moved, its old position would be empty, and then the item below it, if exists, would move up to this empty position. The movement may bring many items forward and even into previous pages, so Tokitsukaze would keep waiting until all the items stop moving, and then do the operation (i.e. check the special page and discard the special items) repeatedly until there is no item need to be discarded.

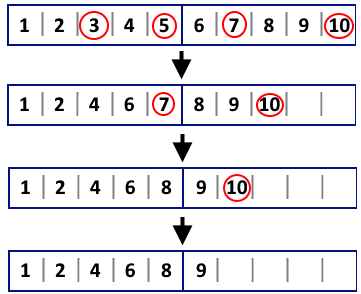Consider the first example from the statement: n=10n=10, m=4m=4, k=5k=5, p=[3,5,7,10]p=[3,5,7,10]. The are two pages. Initially, the first page is special (since it is the first page containing a special item). So Tokitsukaze discards the special items with indices 33 and 55. After, the first page remains to be special. It contains [1,2,4,6,7][1,2,4,6,7], Tokitsukaze discards the special item with index 77. After, the second page is special (since it is the first page containing a special item). It contains [9,10][9,10], Tokitsukaze discards the special item with index 1010.

Tokitsukaze wants to know the number of operations she would do in total.

Input

The first line contains three integers nn, mm and kk (1≤n≤10181≤n≤1018, 1≤m≤1051≤m≤105, 1≤m,k≤n1≤m,k≤n) — the number of items, the number of special items to be discarded and the number of positions in each page.

The second line contains mm distinct integers p1,p2,…,pmp1,p2,…,pm (1≤p1<p2<…<pm≤n1≤p1<p2<…<pm≤n) — the indices of special items which should be discarded.

Output

Print a single integer — the number of operations that Tokitsukaze would do in total.

Examples

input

Copy

10 4 5
3 5 7 10

output

Copy

3

input

Copy

13 4 5
7 8 9 10

output

Copy

1

Note

For the first example:

• In the first operation, Tokitsukaze would focus on the first page [1,2,3,4,5][1,2,3,4,5] and discard items with indices 33 and 55;
• In the second operation, Tokitsukaze would focus on the first page [1,2,4,6,7][1,2,4,6,7] and discard item with index 77;
• In the third operation, Tokitsukaze would focus on the second page [9,10][9,10] and discard item with index 1010.

For the second example, Tokitsukaze would focus on the second page [6,7,8,9,10][6,7,8,9,10] and discard all special items at once.

题意:

一开始有n个数，这些数从1到n编号，每k个数为一组，现在给出m个要删去的特殊数，有一种操作，从第一个包含特殊数的组开始删，一次可以把一组里所有特殊数删掉，删掉数后会有空位，这些空位会被后面的数依次补上，并形成新的组，问最少需要操作多少次

思路:

考虑当前最多可以删到那个数，并求出那个数的坐标，就要知道最大可以到哪个坐标，现在定义一个最大容纳量，
最大容纳量=页数*页容量+删掉的数，页数=1+要再翻多少页（从第1页开始）,
要再翻多少页=（当前坐标-已经删掉的个数-1）/页容量（-1是减去它本身）
一直删到不能再删（已经删的个数要小于等于m且最大坐标要小于等于最大容纳量）
每次统计操作次数

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int amn=1e5+;
 ll n,m,k,sp[amn];
 int main(){
     ios::sync_with_stdio();
     cin>>n>>m>>k;
     for(int i=;i<m;i++)
         cin>>sp[i];
     ll tp=,ans=,jg;
     while(tp<=m){
         jg=((sp[tp]-tp-)/k+)*k+tp;       ///最大容纳量=页数*页容量+删掉的数，页数=1+要再翻多少页（从第1页开始）,要再翻多少页=（当前坐标-已经删掉的个数-1）/页容量（-1是减去它本身）
         while(tp<=m&&sp[tp]<=jg)tp++;      ///一直删到不能再删（已经删的个数要小于等于m且最大坐标要小于等于最大容纳量）
         ans++;
     }
     printf("%lld\n",ans);
 }
 /***
 一开始有n个数，这些数从1到n编号，每k个数为一组，现在给出m个要删去的特殊数，有一种操作，从第一个包含特殊数的组开始删，一次可以把一组里所有特殊数删掉，删掉数后会有空位，这些空位会被后面的数依次补上，并形成新的组，问最少需要操作多少次
 考虑当前最多可以删到那个数，并求出那个数的坐标，就要知道最大可以到哪个坐标，现在定义一个最大容纳量，
 最大容纳量=页数*页容量+删掉的数，页数=1+要再翻多少页（从第1页开始）,
 要再翻多少页=（当前坐标-已经删掉的个数-1）/页容量（-1是减去它本身）
 一直删到不能再删（已经删的个数要小于等于m且最大坐标要小于等于最大容纳量）
 每次统计操作次数
 ***/