Aho-Corasick (AC) 自动机

基础：AC自动机是建立在 trie 树和 kmp 基础之上的，为什么这么说，因为AC自动机是基于字典树的数据结构之上的，其次它是一个自动机，用到了 kmp 的失配数组的思想。

应用：在模式匹配的问题中，如果模板有很多个，可以用AC自动机来求解。

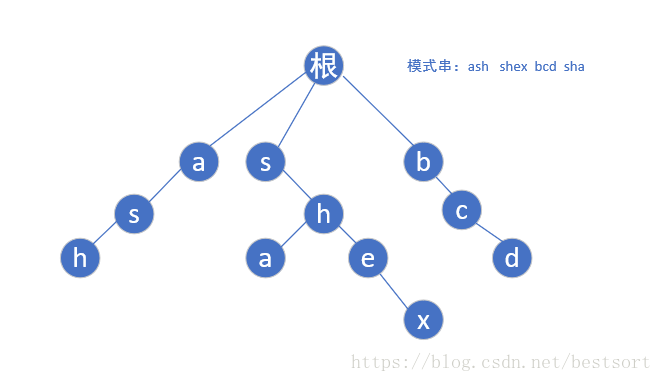
结构：字典树结构：

Fail数组（失配数组）：如果现在已经匹配到一个结点，如果匹配失败，则将指正转移到 Fail 指针指向的地方，这样就不用回溯而直接匹配下去了。（举个例子：如abce和bcd,我们找到c发现下一个要找的不是e,就跳到bcd中的c处,看看此处的下一个字符(d)是不是应该找的那一个）。由此可见， Fail 数组可用一个 BFS 求得。

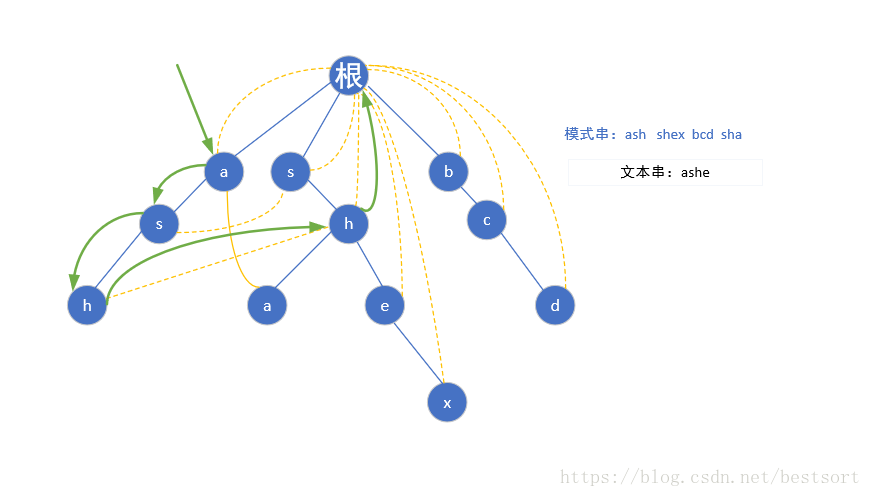
上上图的 Fail 数组指向图：

以ashe为例:其匹配过程如下：

说了这么多，下面直接上模板：

建树：

const int maxn =  2e6+10;
int tree[maxn][26];  //字典树
int point[maxn];  	//记录该单词出现次数
int Fail[maxn];     //失败时的回溯指针
int tot = 0;		//结点个数
void insert(char *s)				//同字典树；建树
{
    int root = 0;
    int len=strlen(s);
    for(int i=0;i<len;i++){
        int id = s[i] - 'a';
        if(!tree[root][id])
            tree[root][id] = ++tot;
        root = tree[root][id];
    }
    point[root]++;      			//当前节点单词数+1
}

求 Fail 数组（ BFS ）：

void getFail()						//求Fail（失配）数组
{
    Fail[0]=0;
    queue <int>q;
    for(int i=0;i<26;i++)		   //将第二层所有出现了的字母扔进队列
    {
        if(tree[0][i]){
            Fail[tree[0][i]] = 0;	//第一层结点肯定全都指向根节点
            q.push(tree[0][i]);
        }
    }

// fail[now]    -> 当前节点now的失败指针指向的地方
// tire[now][i] -> 下一个字母为i+'a'的节点的下标为tire[now][i]

    while(!q.empty())
    {
        int now = q.front();
        q.pop();
    	for(int i=0;i<26;i++)		//查询26个字母
        {
        	if(tree[now][i]){		//如果有这个子节点为字母i+'a',则

				//让这个节点的失败指针指向(((他父亲节点)的失败指针所指向的那个节点)的下一个节点)
                //有点绕,为了方便理解特意加了括号

            	Fail[tree[now][i]] = tree[Fail[now]][i];
            	q.push(tree[now][i]);
        	}
        	else	//否则就让当前节点的这个子节点指向当前节点Fail指针的这个子节点
            	tree[now][i] = tree[Fail[now]][i];
    	}
	}
}

查询：

int query(char *s)
{
    int root = 0,ans = 0;
    ine len=strlen(s);
    for(int i=0;i<len;i++)			//遍历文本串
    {
        int id=s[i]-'a';
        root = tree[root][id];  		//从s[i]点开始寻找
        for(int j=now;j && point[j]!=-1;j=Fail[j]){
            //一直向下寻找,直到匹配失败(失败指针指向根或者当前节点已找过).
            ans += point[j];
            point[j] = -1;    //将遍历国后的节点标记,防止重复计算
        }
    }
    return ans;
}

模板AC代码：

#include<bits/stdc++.h>

using namespace std;
const int maxn=2e6+10;
typedef long long ll;
int tree[maxn][27];
int point[maxn],tot=0,Fail[maxn];
char s[10004][55];
char str[1000005];
void insert(char *s)
{
    int len=strlen(s);
    int root=0;
    for(int i=0;i<len;++i)
    {
        int id=s[i]-'a';
        if(!tree[root][id])
            tree[root][id] = ++tot;
        root=tree[root][id];
    }
    point[root]++;
}
void getFail()
{
    Fail[0]=0;
    queue<int> q;
    for(int i=0;i<26;++i)
    {
        if(tree[0][i]){
            Fail[tree[0][i]]=0;
            q.push(tree[0][i]);
        }
    }
    while(!q.empty())
    {
        int now=q.front();
        q.pop();
        for(int i=0;i<26;++i)
        {
            if(tree[now][i]){
                Fail[tree[now][i]]=tree[Fail[now]][i];
                q.push(tree[now][i]);
            }
            else
                tree[now][i]=tree[Fail[now]][i];
        }
    }
}
ll query(char *s)
{
    int root=0,res=0;
    int len=strlen(s);
    for(int i=0;i<len;++i)
    {
        int id=s[i]-'a';
        root=tree[root][id];
        for(int j=root; j && point[j]!=-1;j=Fail[j]){
            res+=point[j];
            point[j]=-1;
        }
    }
    return res;
}
void init()
{
    for(int i=0;i<=tot;++i)
    {
        point[i]=0;
        Fail[i]=0;
        for(int j=0;j<26;++j){
            tree[i][j]=0;
        }
    }
    tot=0;
}

int main()
{
    //ios::sync_with_stdio(false);

    int T;
    scanf("%d",&T);
    memset(point,0,sizeof(point));
    while(T--)
    {
        int n;
        cin>>n;
        for(int i=0;i<n;++i){
            scanf("%s",&s[i]);
            insert(s[i]);
        }
        getFail();
        scanf("%s",&str);
        int res=query(str);
        printf("%d\n",res);
        init();
    }

    system("pause");
    return 0;
}