MATLAB矩阵处理—特殊矩阵

需要掌握

1. MATLAB语言中特殊矩阵
2. MATLAB语言中矩阵的变幻
3. MATLAB语言矩阵如何求值
4. MATLAB语言中特征值与特征向量
5. MATLAB语言中稀疏矩阵

2.1  特殊矩阵

如何建立矩阵？

逐个按行的顺序，输入矩阵的各个元素，全部元素用中括号括起来，同一行的元素用，或者空格分隔，不同行的元素之间用分号（；）分隔。

l  通用性的特殊矩阵——0矩阵，1矩阵，单位矩阵等等

l  用于专门学科的特殊矩阵——范德蒙矩阵，魔方矩阵等等

1．通用的特殊矩阵

 zeros函数：产生全0矩阵，即零矩阵。

 ones函数：产生全1矩阵，即幺矩阵。

 eye函数：产生对角线为1的矩阵。当矩阵是方阵时，得到一个单位矩阵。

 rand函数：产生（0，1）区间均匀分布的随机矩阵。

 randn函数：产生均值为0，方差为1的标准正态分布随机矩阵。

zeros函数的调用格式：

zeros(m)：产生m×m零矩阵。

zeros(m,n)：产生m×n零矩阵。

zeros(size(A))：产生与矩阵A同样大小的零矩阵。   Size返回A的行数和列数

>> A=zeros(2,3)

A = 0     0     0

　　0     0     0

>> zeros(size(reshape(A,3,2)))   // reshape将A转变为三行两列的矩阵，size得到向量3和2

ans = 0     0

　　0     0

　　0     0

例1  产生5阶两位随机整数（10-99）矩阵A，再产生均值为0.6、方差为0.1的5阶正态分布随机矩阵B，验证(A+B)I=IA+BI（I为单位矩阵）。

rand函数：产生(0，1)开区间均匀分布的随机数x。

fix(a+(b-a+1)*x)：产生[a，b]区间上均匀分布的随机整数。

randn函数：产生均值为0、方差为1的标准正态分布随机数x。

μ+σx：得到均值为μ、方差为σ2的随机数。

>> A=fix(10+(99-10+1)*rand(5));

>> B=0.6+sqrt(0.1)*randn(5);

>> C=eye(5);   //产生五阶单位阵

>> (A+B)*C==C*A+B*C

ans =

1     1     1     1     1

1     1     1     1     1

1     1     1     1     1

1     1     1     1     1

1     1     1     1     1

2．用于专门学科的特殊矩阵

(1)魔方矩阵——Magic Square

>> M=magic(3)     //和均为15

M = 8     1     6

　　3     5     7

　　4     9     2

n阶魔方阵由1,2,3,…,n2共n2个整数组成，且每行、每列以及主、副对角线上各n个元素之和都相等。

n阶魔方阵每行每列元素的和为(1+2+3+…+ n^2)/n=(n+n^3)/2

n>2时有很多不同的n阶魔方阵，MATLAB函数magic(n)产生一个特定的魔方阵。

例2  产生8阶魔方阵，求其每行每列元素的和。

>> M=magic(8);

>> sum(M(1,:))  //每列

ans =

　　260

>> sum(M(:,1))   //每行

ans =

　　260

（2）范德蒙矩阵

范德蒙（Vandermonde）矩阵是法国数学家范德蒙提出的一种特殊矩阵。范得蒙矩阵的最后一列全为1，即向量v各元素的零次方，倒数第二列为指定的向量v，即向量v各元素的一次方， 其他各列是其后列与倒数第二列的点乘积。

在MATLAB中，函数vander(V)生成以向量V为基础的范得蒙矩阵。

>> A=vander(1:5)   //以1.2.3.4.5组成的向量为基础。

A = 1     1     1     1     1

　　16     8     4     2     1

　　81    27     9     3     1

　　256    64    16     4     1

　　625   125    25     5     1

范德蒙矩阵常用在各种通信系统的纠错编码中，例如，常用的Reed-Solomon 编码（里德-所罗门编码）即以范德蒙矩阵为基础。

(3) 希尔伯特矩阵

n阶希尔伯特（Hilbert）矩阵的一般形式为：

希尔伯特矩阵的元素为H(i,j)=1/(i+j-1)。

在MATLAB中，生成n阶希尔伯特矩阵的函数是hilb(n)。

>> format rat   //设置输出为有理数输出

>> H=hilb(4)

H = 1              1/2            1/3            1/4

　　1/2            1/3            1/4            1/5

　　1/3            1/4            1/5            1/6

　　1/4            1/5            1/6            1/7

希尔伯特矩阵是著名的病态矩阵，即任何一个元素发生较小的变动，整个矩 阵的值和逆矩阵都会发生很大变化。病态程度和矩阵的阶数相关，随着阶数的增加病态越严重。

(4)托普利兹矩阵、

托普利兹(Toeplitz)矩阵除第一行第一列外，其他元素都与左上角的元素相等，即T(i,j)=T(i-1,i-1)。

toeplitz(x,y): 生成以x为第一列， y为第一行的托普利兹矩阵。

toeplitz(x): 用向量x生成一个对称的托普利兹矩阵。  //x和y均为向量，长度不必相等。

（5）伴随矩阵

设多项式p(x)为anxn+an-1xn-1+…+a1x+a0，则多项式的伴随矩阵是：

p(x)称为A的特征多项式，方程p(x)=0的根称为A的特征值。第一行由系数组成

MATLAB生成伴随矩阵的函数是compan(p)，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂排在后。例如，生成多项式x3-2x2-5x+6的伴随矩阵。

>> p=[1,-2,-5,6];

>> A=compan(p)

A =  2     5    -6

　　1     0     0

　　0     1     0

可以求出伴随矩阵的特征值，该特征值等于多项式方程的根。

(6) 帕斯卡矩阵

根据二项式定理，(x+y)^n展开后的系数随着n的增大组成一个三角形表，这个三角形称为杨辉三角形。 每行代表不同n时的二项式系数

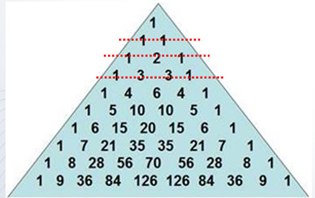
把二项式系数依次填写在矩阵的左侧对角线上，然后提取左侧的n行n列元素即为n阶帕斯卡（Pascal）矩阵。

帕斯卡矩阵的第一行元素和第一列元素都为1，其余位置的元素是该元素的左边元素与上面元素相加，即P(i,j)=P(i,j-1)+P(i-1,j)，且P(i,1)=1,P(1,j)=1。

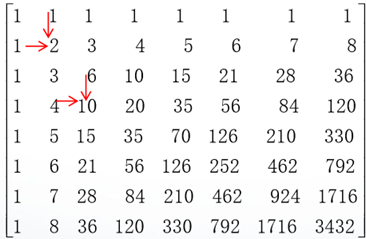
函数pascal(n)生成一个n阶帕斯卡矩阵。

例3  生成5阶帕斯卡矩阵，验证它的逆矩阵的所有元素也为整数。

>> format rat  //有理数输出格式

>> P=pascal(5)

P =

1              1              1              1              1

1              2              3              4              5

1              3              6             10             15

1              4             10             20             35

1              5             15             35             70

>> inv(P)  //求逆矩阵

ans =

5            -10             10             -5              1

-10             30            -35             19             -4

10            -35             46            -27              6

-5             19            -27             17             -4

1             -4              6             -4              1

Tip:单位矩阵：它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。

设A是数域上的一个n阶矩阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E ，则我们称B是A的逆矩阵，而A则被称为可逆矩阵。注：E为单位矩阵。