堆（c++）

5分钟速成堆

FBI⚠WARNING

本文要素过多

吐槽

堆是我迄今为止学过最简单的数据结构

我还没学会最小生成树、最短路时就学会了

堆实用高效，值得推荐

（如果你看完了这篇文章还不会，你可以直接Copy,慢慢理解）

了解什么是堆

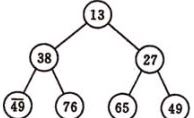
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。————摘自（没人看得懂的）度娘

　　

堆的特性？
堆中某个节点的值总是不大于（大根堆）或不小于（小根堆）其父节点的值；
堆总是一棵完全二叉树。
堆的作用？
堆支持查找最值的操作。
堆的实现
堆有5种操作，上移、下移、插入、删除、建堆。

(本文采用迭代法，如果你难以理解，可以使用递归法)

上移

若比父节点大/小，则与父节点交换（上移）

 //我们以小根堆为例：
 void up(int x){//把x这个位置上移
     while (x>&&c[x]<c[x/]){
         swap(x,x/);//交换
         x/=;//节点变化
     }
     return;
 }

下移

若比子节点大/小，则与子节点交换（下移）

//我们以小根堆为例：
void down(int x){//把x这个位置下移
    while (x*2<=cnt&&c[x]>c[x/2]||x*2+1<=cnt&&c[x]>=c[x*2+1]){
        int y=x*2;
        if (y+1<=cnt&&c[y]>c[y+1]) y++;//尽量选小的换
        swap(x,y);//交换
        x=y;//节点变化
    }
    return;
}

插入

元素会有变化，所以要用到插入

设cnt为堆元素总数，c为堆，则在c[++cnt]插入

但是此时堆不一定保持特性

所以进行上移

维护堆

void down(int x){//插入x
    c[++cnt]=x;
    up(cnt);
    return;
}

　　

删除

当我们要删除最值

就将堆顶弹出（显而易见）

但是特性不一定能保持

所以我们将堆底放到堆顶

再下移

void del(int x){//删除x
    c[1]=c[cnt--];
    down(1);
    return;
}

建堆

无脑暴力：不断插入

O（NlogN)

for (int i=1;i<=n;i++){
	scanf("%d",&x);
	insert(x);
}

　　

优化：处理一半,自然OK

O(N)

for (int i=1;i<=n;i++){
	scanf("%d",&c[i]);
}
for (int i=n/2;i>0;i--)
	down(i);

重中之重（c++福利）

c++有优先队列（堆）

可以直接调用函数

大家可以自学

例题

排序（经典堆排序）

code如下（pascal，code来自jzoj.net，a是堆，num是堆元素总数）

var
num,i,j,k,m,n,x,y:longint;
a:array[0..200001]of longint;
procedure up(x:longint);
var
i,sw:longint;
begin
    while(a[x div 2]>a[x])and(x>1)do
    begin
        sw:=a[x div 2];
	a[x div 2]:=a[x];
	a[x]:=sw;
        x:=x div 2;
    end;
end;
procedure down(x:longint);
var
i,t:longint;
begin
   while(2*x<=num)and(a[x]>a[2*x])or(2*x+1<=num)and(a[x]>=a[2*x+1]) do
   begin
       i:=2*x;
       if(i+1<=num)and(a[i+1]<a[i]) then inc(i);
       t:=a[x];
       a[x]:=a[i];
       a[i]:=t;
       x:=i;
   end;
end;

begin
    read(m);
    for i:=1 to m do
    begin
        inc(num);read(a[num]);up(num);
    end;
    for i:=1 to m do
    begin
        writeln(a[1],' ');
        a[1]:=a[num];   a[num]:=0;
        dec(num);
        down(1);
    end;
end.

思路：首先建一个堆，然后每次取出堆顶并输出，然后删除堆顶

O（NlogN）

合并果子

一堆果子，有权值，每次合并，则权值为合并果子权值和，耗费体力相同

问体力消耗最小值

本题用贪心，每次将最小的两堆果子合并

用堆实现

弹出堆顶，维护之

再取堆顶，堆顶等于两次权值和

并且再次维护

经典贪心

code（code来自jzoj.net，heap是堆，heap_size是堆元素总数）

#include <cstdio>
using namespace std;
int heap_size,n;
int heap[30001];
void swap(int &a,int &b){int t=a;a=b;b=t;}
void put(int d){
	int now,next;
	heap[++heap_size]=d;
	now=heap_size;
	while(now>1){
		next=now>>1;
		if(heap[now]>=heap[next]) return;
		swap(heap[now],heap[next]);
				now=next;
	}
}
int get(){
	int now,next,res;
	res=heap[1];
	heap[1]=heap[heap_size--];
	now=1;
	while(now*2<=heap_size){
		next=now*2;
		if(next<heap_size&&heap[next+1]<heap[next]) next++;
		if(heap[now]<=heap[next]) return res;
		swap(heap[now],heap[next]);
		now=next;
	}
	return res;
}
void work(){
	int i,x,y,ans=0;
	scanf("%d",&n);
	for(i=1;i<=n;i++){
		scanf("%d",&x);
		put(x);
	}
	for(i=1;i<n;i++){
		x=get();
		y=get();
		ans+=x+y;
		put(x+y);
	}
	printf("%d",ans);
}
int main(){
	work();
	return 0;
}

顺手点个赞