scikit-learn中的岭回归（Ridge Regression）与Lasso回归

一、岭回归模型

　　岭回归其实就是在普通最小二乘法回归（ordinary least squares regression）的基础上，加入了正则化参数λ。

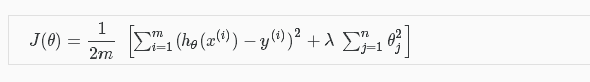
二、如何调用

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto')

alpha：就是上述正则化参数λ；
fit_intercept：默认为true，数据可以拦截，没有中心化；
normalize：输入的样本特征归一化，默认false；
copy_X：复制或者重写；
max_iter：最大迭代次数；
tol: 控制求解的精度；
solver：求解器，有auto, svd, cholesky, sparse_cg, lsqr几种，一般我们选择auto，一些svd，cholesky也都是稀疏表示中常用的omp求解算法中的知识，大家有时间可以去了解。

Ridge函数会返回一个clf类，里面有很多的函数，一般我们用到的有：
clf.fit(X, y)：输入训练样本数据X，和对应的标记y；
clf.predict(X)：利用学习好的线性分类器，预测标记，一般在fit之后调用；
clf.corf_: 输入回归表示系数

详见：

http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Ridge.html#sklearn.linear_model.Ridge.decision_function

三、Lasso模型（Least absolute shrinkage and selection operator-最小绝对收缩与选择算子）

　　Lasso构造的是一个一阶的惩罚函数，满足L1范数，从而使得模型的一些变量参数可能为0（岭回归系数为0的可能性非常低），得到的模型更为精炼。

　　Lasso的正则化惩罚函数形式是L1范数，属于绝对值形式，L1范数的好处是当lambda充分大时可以把某些待估参数精确地收缩到0。回归的参数估计经常会有为0的状况，对于这种参数，我们便可以选择对它们进行剔除，就不用我们进行人工选择剔除变量，而可以让程序自动根据是否为0来剔除掉变量了。剔除了无用变量后，可能会使的模型效果更好，因为会存在一些关联比较大的共线变量，从这个角度来看，Lasso回归要优于岭回归。

　　scikit-learn对lasso模型的调用与上述岭回归调用大同小异，详见：

　　http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html