《机器学习实战》笔记——决策树（ID3）

闲来无事最近复习了一下ID3决策树算法，并凭着理解用pandas实现了一遍。对pandas更熟悉的朋友可供参考（链接如下）。相比本篇博文，更简明清晰，更适合复习用。

https://github.com/DianeSoHungry/ShallowMachineLearningCodeItOut/blob/master/ID3.ipynb

现在要介绍的是ID3决策树算法，只适用于标称型数据，不适用于数值型数据。

决策树学习算法最大的优点是，他可以自学习，在学习过程中，不需要使用者了解过多的背景知识、领域知识，只需要对训练实例进行较好的标注就可以自学习了。

建立决策树的关键在于当前状态下选择哪一个属性作为分类依据，根据不同的目标函数，有三种主要的算法：

ID3(Iterative Dichotomiser)

C4.5

CART(Classification And Regression Tree)

问题描述：

下面是一个小型的数据集，5条记录，2个特征（属性），有标签。

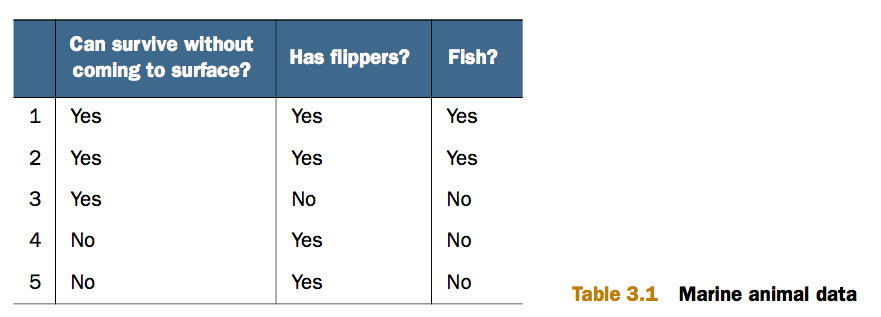
根据这个数据集，我们可以建立如下决策树（用matplotlib的注释功能画的）。

观察决策树，决策节点为特征，其分支为决策节点的各个不同取值，叶节点为预测值。

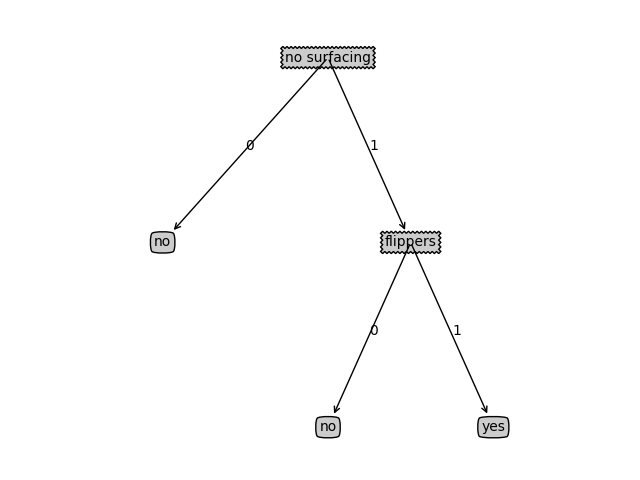
建树结束也就是建立好了一个决策树分类器，有了分类器，就可以根据这个分类器对其他的鱼进行预测了。预测准确性今天暂且不讨论。

那么如何建立这样的决策树呢？

第一步：建立决策树。

1.1 利用信息增益寻找当前最佳分类特征

想象现在你是一个判断结点，你从头顶的分支上获得了一个数据集，表中包含标签和若干属性。你现在要根据某个属性来对你接收到的数据集进行分组。到底用哪个属性来作为划分依据呢？

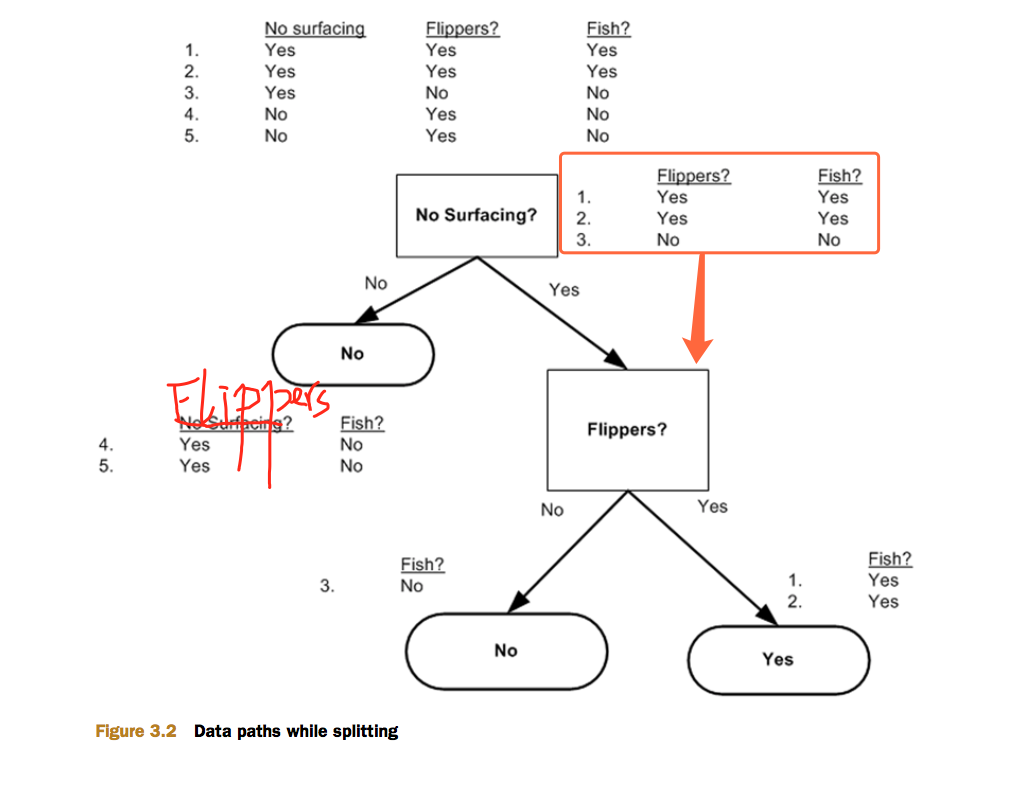
我们用信息增益来选择某个节点上用哪个特征来进行分类。

什么是信息？

如果待分类的事物可能划分在多个分类中，则每个分类x_i的信息定义为：

（这里log前面应该有个负号。）

什么是香农熵？

香农熵是所有类别所有可能类别信息的期望值，即：

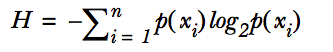
什么是信息增益？

信息增益=原香农熵-新香农熵

注意：新香农熵为按照某特征划分之后，每个分支数据集的香农熵之和。

可以这样想：香农熵相当于数据类别（标签）的混乱程度，信息增益可以衡量划分数据集前后数据（标签）向有序性发展的程度。因此，回到怎样利用信息增益寻找当前最佳分类特征的话题，假如你是一个判断节点，你拿来一个数据集，数据集里面有若干个特征，你需要从中选取一个特征，使得信息增益最大（注意：将数据集中在该特征上取值相同的记录划分到同一个分支，得到若干个分支数据集，每个分支数据集都有自己的香农熵，各个分支数据集的香农熵的期望才是新香农熵）。要找到这个特征只需要将数据集中的每个特征遍历一次，求信息增益，取获得最大信息增益的那个特征。

代码如下（其中，calcShannonEnt(dataSet)函数用来计算数据集dataSet的香农熵，splitDataSet(dataSet, axis, value)函数将数据集dataSet的第axis列中特征值为value的记录挑出来，组成分支数据集返回给函数。这两个函数后面会给出函数定义。）：

 # 3-3 选择最好的'数据集划分方式'（特征）
 # 一个一个地试每个特征，如果某个按照某个特征分类得到的信息增益（原香农熵-新香农熵）最大，
 # 则选这个特征作为最佳数据集划分方式
 def chooseBestFeatureToSplit(dataSet):
     numFeatures = len(dataSet[0]) - 1
     baseEntropy = calcShannonEnt(dataSet)
     bestInfoGain = 0.0
     bestFeature = -1
     for i in range(numFeatures):
         featList = [example[i] for example in dataSet]
         uniqueVals = set(featList)
         newEntropy = 0.0
         for value in uniqueVals:
             subDataSet = splitDataSet(dataSet, i, value)
             prob = len(subDataSet) / float(len(dataSet))
             newEntropy += prob * calcShannonEnt(subDataSet)
         infoGain = baseEntropy - newEntropy
         if (infoGain > bestInfoGain):
             bestInfoGain = infoGain
             bestFeature = i
     return bestFeature

calcShannonEnt(dataSet)函数代码：

 def calcShannonEnt(dataSet):
     numEntries = len(dataSet)    # 总记录数
     labelCounts = {}    # dataSet中所有出现过的标签值为键，相应标签值出现过的次数作为值
     for featVec in dataSet:
         currentLabel = featVec[-1]
         labelCounts[currentLabel] = labelCounts.get(currentLabel, 0) + 1
     shannonEnt = 0.0
     for key in labelCounts:
         prob = -float(labelCounts[key])/numEntries
         shannonEnt += prob * log(prob, 2)
     return shannonEnt

splitDataSet(dataSet, axis, value)函数代码：

 # 3-2 按照给定特征划分数据集（在某个特征axis上，值等于value的所有记录
 # 组成新的数据集retDataSet，新数据集不需要axis这个特征，注意value是特征值，axis指的是特征（所在的列下标））
 def splitDataSet(dataSet, axis, value):
     retDataSet = []
     for featVec in dataSet:
         if featVec[axis] == value:
             reducedFeatVec = featVec[:axis]
             reducedFeatVec.extend(featVec[axis+1:])
             retDataSet.append(reducedFeatVec)
     return retDataSet

1.2 建树

建树是一个递归的过程。

递归结束的标志（判断某节点是叶节点的标志）：

情况1. 分到该节点的数据集中，所有记录的标签列取值都一样。

或

情况2. 分到该节点的数据集中，只剩下标签列。

a. 经判断，若是叶节点，则：

对应情况1，返回数据集中第一条记录的标签值（反正所有标签值都一样）。

对应情况2，返回数据集中所有标签值中，出现次数最多的那个标签值（代码中，定义一个函数majorityCnt(classList)来实现）

b. 经判断，若不是叶节点，则：

step1. 建立一个字典，字典的键为该数据集上选出的最佳特征（划分依据）。

step2. 将具有相同特征值的记录组成新的数据集（利用splitDataSet(dataSet, axis, value)函数实现，注意期间抛弃了当前用于划分数据的特征列），对新的数据集们进行递归建树。

建树代码：

 # 3-4 创建树的函数代码
 # 如果非叶子结点，则以当前数据集建树，并返回该树。该树的根节点是一个字典，键为划分当前数据集的最佳特征，值为按照键值划分后各个数据集构造的树
 # 叶子节点有两种：1.只剩没有特征时，叶子节点的返回值为所有记录中，出现次数最多的那个标签值 2.该叶子节点中，所有记录的标签相同。

 def createTree(dataSet, labels): #label向量的维度为特征数，不是记录数，是不同列下标对应的特征
     classList = [example[-1] for example in dataSet]
     if classList.count(classList[0]) == len(classList):
         return classList[0]
     if len(dataSet[0]) == 1:
         return majorityCnt(classList)
     bestFeat = chooseBestFeatureToSplit(dataSet)
     bestFeatLabel = labels[bestFeat]
     myTree = {bestFeatLabel: {}}
     del(labels[bestFeat])
     featValues = [example[bestFeat] for example in dataSet]
     uniqueVals = set(featValues)
     for value in uniqueVals:  #递归建子树,若值为字典，则非叶节点，若为字符串，则为叶节点
         myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), labels)
     return myTree

用上面给出的数据来建立一颗决策树做示范：

在同一个程序中输入如下代码并运行：

 def createDataSet():
     dataSet = [[1, 1, 'yes'],
                [1, 1, 'yes'],
                [1, 0, 'no'],
                [0, 1, 'no'],
                [0, 1, 'no']]
     labels = ['no surfacing', 'flippers']
     return dataSet, labels

 myDat, labels = createDataSet()
 myTree = createTree(myDat, labels)
 print myTree

运行结果为：

{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}

若利用后面画决策树的代码可以画出这颗决策树：

案例：

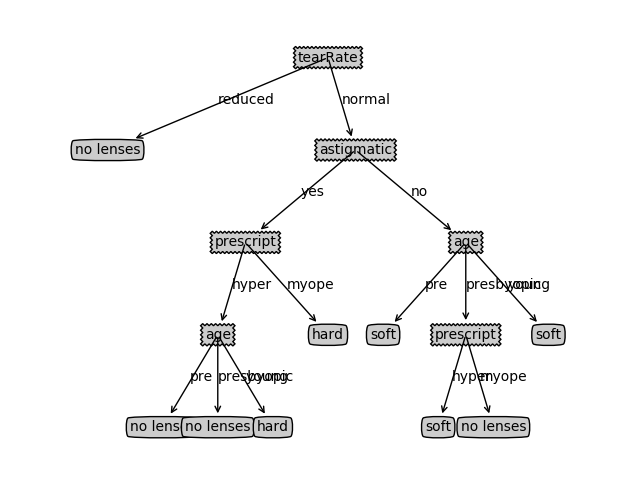
我们通过建立决策树来预测患者需要佩戴哪种隐形眼镜（soft(软材质)、hard(硬材质)、no lenses(不适合硬性眼睛）），数据集包含下面几个特征：age（年龄）, prescript（近视还是远视）, astigmatic（散光）, tearRate（眼泪清除率）

建树的结果为：

{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic': {'yes': {'prescript': {'hyper': {'age': {'pre': 'no lenses', 'presbyopic': 'no lenses', 'young': 'hard'}}, 'myope': 'hard'}}, 'no': {'age': {'pre': 'soft', 'presbyopic': {'prescript': {'hyper': 'soft', 'myope': 'no lenses'}}, 'young': 'soft'}}}}}}

画出来是这个样子：

画决策树的代码（不讲）

涉及matplotlib.pyplot模块中的annotation的用法，点击链接进入官网学习这块内容的prerequisite。

 # _*_coding:utf-8_*_

 # 3-7 plotTree函数
 import matplotlib.pyplot as plt

 # 定义节点和箭头格式的常量
 decisionNode = dict(boxstyle="sawtooth", fc="0.8")
 leafNode = dict(boxstyle="round4", fc="0.8")
 arrow_args = dict(arrowstyle="<-")

 def plotMidTest(cntrPt, parentPt,txtString):
     xMid = (parentPt[0] + cntrPt[0])/2.0
     yMid = (parentPt[1] + cntrPt[1])/2.0
     createPlot.ax1.text(xMid, yMid, txtString)

 # 绘制自身
 # 若当前子节点不是叶子节点，递归
 # 若当子节点为叶子节点，绘制该节点
 def plotTree(myTree, parentPt, nodeTxt):
     numLeafs = getNumLeafs(myTree)
     # depth = getTreeDepth(myTree)
     firstStr = myTree.keys()[0]
     cntrPt = (plotTree.xoff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yoff)
     plotMidTest(cntrPt, parentPt, nodeTxt)
     plotNode(firstStr, cntrPt, parentPt, decisionNode)
     secondDict = myTree[firstStr]
     plotTree.yoff = plotTree.yoff - 1.0/plotTree.totalD
     for key in secondDict.keys():
         if type(secondDict[key]).__name__=='dict':
             plotTree(secondDict[key], cntrPt, str(key))
         else:
             plotTree.xoff = plotTree.xoff + 1.0/plotTree.totalW
             plotNode(secondDict[key], (plotTree.xoff, plotTree.yoff), cntrPt, leafNode)
             plotMidTest((plotTree.xoff, plotTree.yoff), cntrPt, str(key))
     plotTree.yoff = plotTree.yoff + 1.0/plotTree.totalD

 # figure points
 # 画结点的模板
 def plotNode(nodeTxt, centerPt, parentPt, nodeType):
     createPlot.ax1.annotate(nodeTxt,  # 注释的文字，（一个字符串）
                             xy=parentPt,  # 被注释的地方（一个坐标）
                             xycoords='axes fraction',  # xy所用的坐标系
                             xytext=centerPt,  # 插入文本的地方（一个坐标）
                             textcoords='axes fraction', # xytext所用的坐标系
                             va="center",
                             ha="center",
                             bbox=nodeType,  # 注释文字用的框的格式
                             arrowprops=arrow_args)  # 箭头属性

 def createPlot(inTree):
     fig = plt.figure(1, facecolor='white')
     fig.clf()
     axprops = dict(xticks=[], yticks=[])
     createPlot.ax1 = plt.subplot(111,frameon=False, **axprops)
     plotTree.totalW = float(getNumLeafs(inTree))
     plotTree.totalD = float(getTreeDepth(inTree))
     plotTree.xoff = -0.5/plotTree.totalW
     plotTree.yoff = 1.0

     plotTree(inTree, (0.5, 1.0),'') #树的引用作为父节点，但不画出来，所以用''
     plt.show()

 def getNumLeafs(myTree):
     numLeafs = 0
     firstStr = myTree.keys()[0]
     secondDict = myTree[firstStr]
     for key in secondDict.keys():
         if type(secondDict[key]).__name__ =='dict':
             numLeafs += getNumLeafs(secondDict[key])
         else:
             numLeafs += 1
     return numLeafs

 # 子树中树高最大的那一颗的高度+1作为当前数的高度
 def getTreeDepth(myTree):
     maxDepth = 0    #用来记录最高子树的高度+1
     firstStr = myTree.keys()[0]
     secondDict = myTree[firstStr]
     for key in secondDict.keys():
         if type(secondDict[key]).__name__ == 'dict':
             thisDepth = 1 + getTreeDepth(secondDict[key])
         else:
             thisDepth = 1
         if(thisDepth > maxDepth):
             maxDepth = thisDepth
     return maxDepth

 # 方便测试用的人造测试树
 def retrieveTree(i):
     listofTrees = [{'no surfacing':{0:'no',1:{'flippers':{0:'no',1:'yes'}}}},
                    {'no surfacing':{0:'no',1:{'flippers':{0:{'head':{0:'no',1:'yes'}},1:'no'}}}}
                    ]
     return listofTrees[i]