数据结构&算法（一）_堆、栈（堆栈）、队列、链表

堆：

①堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

·堆中某个节点的值总是不大于或不小于其父节点的值；

·堆总是一棵完全二叉树。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。

②堆是在程序运行时，而不是在程序编译时，申请某个大小的内存空间。即动态分配内存，对其访问和对一般内存的访问没有区别。

③堆是应用程序在运行的时候请求操作系统分配给自己内存，一般是申请/给予的过程。

④堆是指程序运行时申请的动态内存，而栈只是指一种使用堆的方法(即先进后出)。

堆的应用：

#堆排序
def sift(li, left, right):
    i = left
    j = 2 * i + 1
    tmp = li[left]
    while j <= right:
        if j+1 <= right and li[j] < li[j+1]:
            j = j + 1
        if tmp < li[j]:
            li[i] = li[j]
            i = j
            j = 2 * i + 1
        else:
            break
    li[i] = tmp
 
def heap_sort(li):
    n = len(li)
    for i in range(n//2-1, -1, -1): #建立堆
        sift(li, i, n-1)
 
    for i in range(n-1, -1, -1):   #挨个出数
        li[0], li[i] = li[i],li[0]
        sift(li, 0, i-1)
 
li = [6,8,1,9,3,0,7,2,4,5]
heap_sort(li)
print(li)

　　

栈：

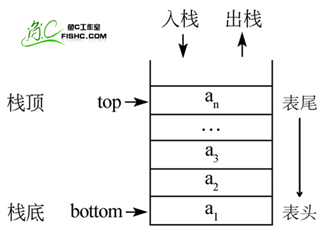
①栈（stack）又名堆栈，一个数据集合，可以理解为只能在一端进行插入或删除操作的列表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。

②栈就是一个桶，后放进去的先拿出来，它下面本来有的东西要等它出来之后才能出来（先进后出）

③栈(Stack)是操作系统在建立某个进程时或者线程（在支持多线程的操作系统中是线程）为这个线程建立的存储区域，该区域具有FIFO的特性，在编译的时候可以指定需要的Stack的大小。

栈的基本操作：
　　进栈（压栈）：push
　　出栈：pop
　　取栈顶：gettop

用python实现堆栈

# 后进先出
class Stack():
    def __init__(self,size):
        self.size=size
        self.stack=[]
        self.top=-1
 
    def push(self,x):
        if self.isfull():
            raise exception("stack is full")
        else:
            self.stack.append(x)
            self.top=self.top+1
 
    def pop(self):
        if self.isempty():
            raise exception("stack is empty")
        else:
            self.top=self.top-1
            self.stack.pop()
 
    def isfull(self):
        return self.top+1 == self.size
    def isempty(self):
        return self.top == '-1'
    def showStack(self):
        print(self.stack)
 
s=Stack(10)
for i in range(5):
    s.push(i)
s.showStack()
for i in range(3):
    s.pop()
s.showStack()
 
"""
类中有top属性，用来指示栈的存储情况，初始值为1，一旦插入一个元素，其值加1，利用top的值乐意判定栈是空还是满。
执行时先将0,1,2,3,4依次入栈，然后删除栈顶的前三个元素
"""

栈的应用——括号匹配问题

括号匹配问题：给一个字符串，其中包含小括号、中括号、大括号，求该字符串中的括号是否匹配。例如：
()()[]{}    匹配
([{()}])    匹配
[](          不匹配
[(])        不匹配

def kuohao_match(exp):
    stack = []
    di = {'(':')', '{':'}', '[':']'}
    for c in exp:
        if c in {'(','{', '['}:
            stack.append(c)
        else:
            if len(stack) == :
                return False
            top = stack.pop()
            if di[top] != c:
                return False
    if len(stack) > :
        return False
    else:
        return True
 
print(kuohao_match('()[]{([]][]}()'))

栈的应用——括号匹配问题

栈的应用——迷宫问题

'''
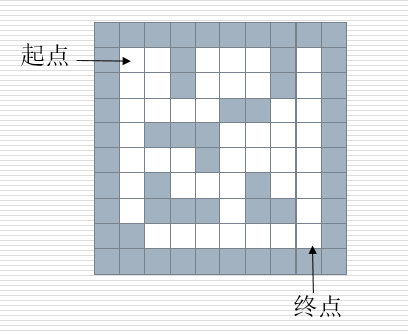
解决思路
在一个迷宫节点(x,y)上，可以进行四个方向的探查：maze[x-][y], maze[x+][y], maze[x][y-], maze[x][y+]
思路：从一个节点开始，任意找下一个能走的点，当找不到能走的点时，退回上一个点寻找是否有其他方向的点。
方法：创建一个空栈，首先将入口位置进栈。当栈不空时循环：获取栈顶元素，寻找下一个可走的相邻方块，如果找不到可走的相邻方块，说明当前位置是死胡同，进行回溯（就是讲当前位置出栈，看前面的点是否还有别的出路）
 
'''
 
maze = [
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,]
]
 
dirs = [lambda x, y: (x + , y),
        lambda x, y: (x - , y),
        lambda x, y: (x, y - ),
        lambda x, y: (x, y + )]
 
def mpath(x1, y1, x2, y2):
    stack = []
    stack.append((x1, y1))
    while len(stack) > :
        curNode = stack[-]
        if curNode[] == x2 and curNode[] == y2:
            #到达终点
            for p in stack:
                print(p)
            return True
        for dir in dirs:
            nextNode = dir(curNode[], curNode[])
            if maze[nextNode[]][nextNode[]] == :
                #找到了下一个
                stack.append(nextNode)
                maze[nextNode[]][nextNode[]] = -  # 标记为已经走过，防止死循环
                break
        else:#四个方向都没找到
            maze[curNode[]][curNode[]] = -  # 死路一条,下次别走了
            stack.pop() #回溯
    print("没有路")
    return False
 
mpath(,,,)

栈的应用__迷宫问题

队列

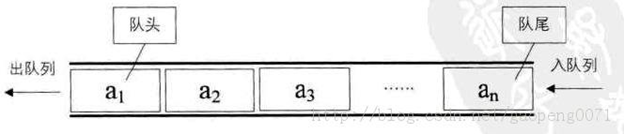
• 队列(Queue)是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。
• 　　进行插入的一端称为队尾(rear)，插入动作称为进队或入队
• 　　进行删除的一端称为队头(front)，删除动作称为出队
• 队列的性质：先进先出(First-in, First-out)
• 双向队列：队列的两端都允许进行进队和出队操作

使用方法：from collections import deque
创建队列：queue = deque(li)
进队：append
出队：popleft
双向队列队首进队：appendleft
双向队列队尾进队：pop

队列的实现原理

队列的实现原理：环形队列

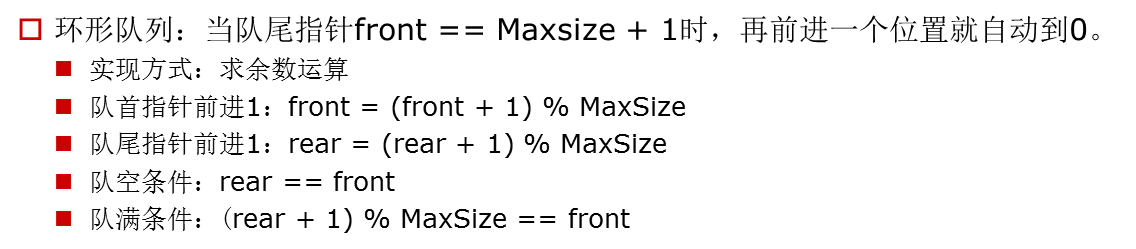
队列的应用：

'''
思路：从一个节点开始，寻找所有下面能继续走的点。继续寻找，直到找到出口。
方法：创建一个空队列，将起点位置进队。在队列不为空时循环：出队一次。如果当前位置为出口，则结束算法；否则找出当前方块的4个相邻方块中可走的方块，全部进队。
 
'''
 
from collections import deque
 
mg = [
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,],
    [,,,,,,,,,]
]
 
dirs = [lambda x, y: (x + , y),
        lambda x, y: (x - , y),
        lambda x, y: (x, y - ),
        lambda x, y: (x, y + )]
 
def print_p(path):
    curNode = path[-]
    realpath = []
    print('迷宫路径为：')
    while curNode[] != -:
        realpath.append(curNode[:])
        curNode = path[curNode[]]
    realpath.append(curNode[:])
    realpath.reverse()
    print(realpath)
 
def mgpath(x1, y1, x2, y2):
    queue = deque()
    path = []
    queue.append((x1, y1, -))
    mg[x1][y1] = -
    while len(queue) > :
        curNode = queue.popleft()
        path.append(curNode)
        if curNode[] == x2 and curNode[] == y2:
            #到达终点
            # for i,j,k in path:
            #     print("(%s,%s) %s"%(i,j,k))
            print_p(path)
            return True
        for dir in dirs:
            nextNode = dir(curNode[], curNode[])
            if mg[nextNode[]][nextNode[]] == :  # 找到下一个方块
                queue.append((nextNode[], nextNode[], len(path) - ))
                mg[nextNode[]][nextNode[]] = -  # 标记为已经走过
    return False
 
mgpath(,,,)

队列的应用--队列解决迷宫问题

链表

　　链表中每一个元素都是一个对象，每个对象称为一个节点，包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接，最终串联成一个链表。

节点的定义：

class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None

头节点：

链表的遍历：

#遍历链表
def traversal(head):
    curNode = head #临时用指针
    while cueNode is not None:
        print(curNode.data)
        curNode = curNode.Next

　　

链表节点的插入和删除

插入：
p.next = curNode.next
curNode.next = p
 
删除：
p = curNode.next
curNode.next = curNode.next.next
del p

　　

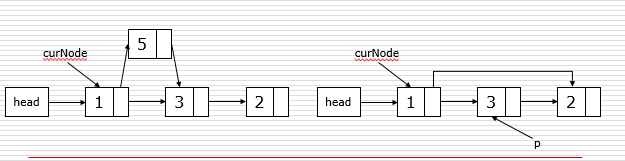
建立链表

#头插法：
def createLinkListF(li):
    l = Node()
    for num in li:
        s = Node(num)
        s.next = l.next
        l.next = s
    return l

#尾插法
def createLinkListR(li):
    l = Node()
    r = l       #r指向尾节点
    for num in li:
        s = Node(num)
        r.next = s
        r = s

双链表

双链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点。
节点定义：

class Node(object):
    def __init__(self, item=None):
        self.item = item
        self.next = None
        self.prior = None

双链表的插入和删除

#插入：
p.next = curNode.next
curNode.next.prior = p
p.prior = curNode
curNode.next = p
 
#删除：
p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p

　　

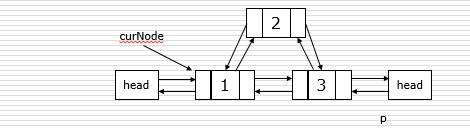
建立双链表

def createLinkListR(li):
    l = Node()
    r = l
    for num in li:
        s = Node(num)
        r.next = s
        s.prior = r
        r = s
    return l, r

　　

栈与队列的异同

栈（Stack）和队列（Queue）是两种操作受限的线性表。

（线性表：线性表是一种线性结构，它是一个含有n≥0个结点的有限序列，同一个线性表中的数据元素数据类型相同并且满足“一对一”的逻辑关系。

“一对一”的逻辑关系指的是对于其中的结点，有且仅有一个开始结点没有前驱但有一个后继结点，有且仅有一个终端结点没有后继但有一个前驱结点，其它的结点都有且仅有一个前驱和一个后继结点。）

这种受限表现在：栈的插入和删除操作只允许在表的尾端进行（在栈中成为“栈顶”），满足“FIFO：First In Last Out”；队列只允许在表尾插入数据元素，在表头删除数据元素,满足“First In First Out”。

栈与队列的相同点：

1.都是线性结构。

2.插入操作都是限定在表尾进行。

3.都可以通过顺序结构和链式结构实现。、

4.插入与删除的时间复杂度都是O（1），在空间复杂度上两者也一样。

5.多链栈和多链队列的管理模式可以相同。

栈与队列的不同点：

1.删除数据元素的位置不同，栈的删除操作在表尾进行，队列的删除操作在表头进行。

2.应用场景不同；常见栈的应用场景包括括号问题的求解，表达式的转换和求值，函数调用和递归实现，深度优先搜索遍历等；常见的队列的应用场景包括计算机系统中各种资源的管理，消息缓冲器的管理和广度优先搜索遍历等。

3.顺序栈能够实现多栈空间共享，而顺序队列不能。